decompose F(x)=((nx^n )/(x^(2n) +1)) inside C(x) and R(x) (n≥2) and determine ∫


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 79108 by mathmax by abdo last updated on 22/Jan/20

$d e c o m p o s e F (x) = \frac{{n x}^{n}}{x^{2 n} + 1} i n s i d e C (x) a n d R (x) (n ⩾ 2)$ $a n d d e t e r m i n e \int_{0}^{+ \infty} F (x) d x$
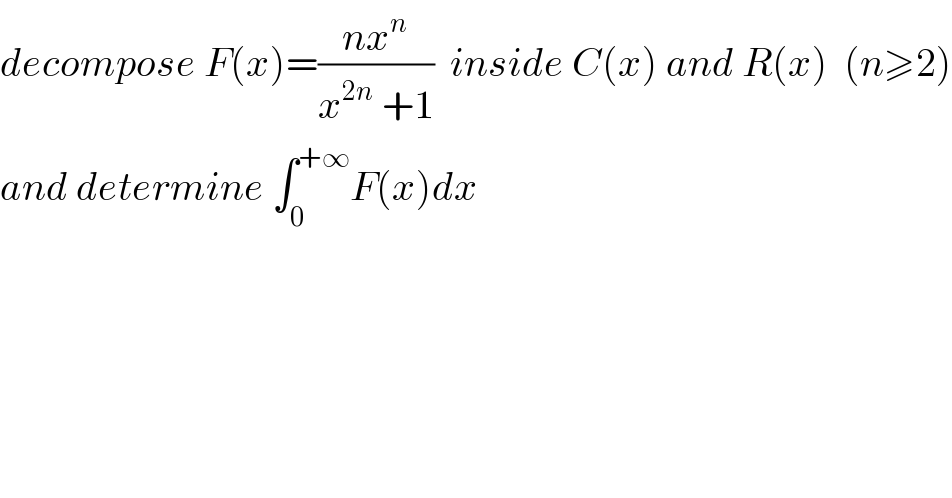
Commented by mathmax by abdo last updated on 31/Jan/20
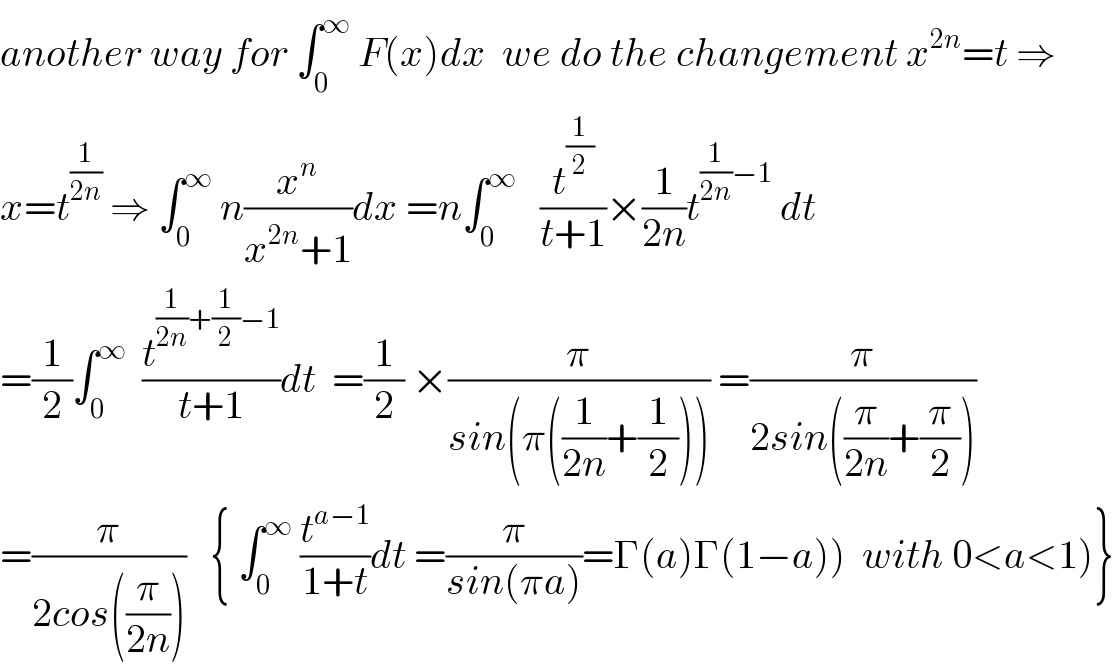
$another way for ∫_0 ^∞ F(x)dx we do the changement x^(2n) =t ⇒ x=t^(1/(2n)) ⇒ ∫_0 ^∞ n(x^n /(x^(2n) +1))dx =n∫_0 ^∞ (t^(1/2) /(t+1))×(1/(2n))t^((1/(2n))−1) dt =(1/2)∫_0 ^∞ (t^((1/(2n))+(1/2)−1) /(t+1))dt =(1/2) ×(π/(sin(π((1/(2n))+(1/2))))) =(π/(2sin((π/(2n))+(π/2)))) =(π/(2cos((π/(2n))))) { ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa)))=Γ(a)Γ(1−a)) with 0<a<1)}$
$a n o t h e r w a y f o r \int_{0}^{\infty} F (x) d x w e d o t h e c h a n g e m e n t x^{2 n} = t \Rightarrow$ $x = t^{\frac{1}{2 n}} \Rightarrow \int_{0}^{\infty} n \frac{x^{n}}{x^{2 n} + 1} d x = n \int_{0}^{\infty} \frac{t^{\frac{1}{2}}}{t + 1} \times \frac{1}{2 n} t^{\frac{1}{2 n} - 1} d t$ $= \frac{1}{2} \int_{0}^{\infty} \frac{t^{\frac{1}{2 n} + \frac{1}{2} - 1}}{t + 1} d t = \frac{1}{2} \times \frac{π}{s i n (π (\frac{1}{2 n} + \frac{1}{2}))} = \frac{π}{2 s i n (\frac{π}{2 n} + \frac{π}{2})}$ $= \frac{π}{2 c o s (\frac{π}{2 n})} {\int_{0}^{\infty} \frac{t^{a - 1}}{1 + t} d t = \frac{π}{s i n (π a)} = Γ (a) Γ (1 - a)) w i t h 0 < a < 1)}$
	Answered by mind is power last updated on 22/Jan/20
	$over C(x) x^(2n) +1=0⇒x^(2n) =−1=e^(iπ+2kπ) x_k =e^(((i(1+2k)π)/(2n)) ) ,k∈[0,2n−1] x_(2n−k−1) =e^(i(((1+2(2n−k−1))/(2n)))π) =e^(−i(((1+2k)/(2n)))π) ⇒x_k =x_(2n−1−k) ^− ,E ((nx^n )/(x^(2n) +1))=Σ(a_k /(x−x_k )) a_k =((nx_k )/(2nx_k ^(2n−1) ))=(1/(2x_k ^(2n−2) ))=−(x_k ^2 /2) ((nx^n )/(x^(2n) +1))=−(1/2)Σ_(k=0) ^(2n−1) (x_k ^2 /((x−x_k ))) over R(X) −(1/2)Σ_(k=0) ^(2n−1) (x_k ^2 /((x−x_k )))=−(1/2).{Σ_(k=0) ^(n−1) (x_k ^2 /(x−x_k ))+Σ_(k=n) ^(2n−1) (x_k ^2 /(x−x_k ))} =−(1/2){Σ_(k=0) ^(n−1) [(x_k ^2 /(x−x_k ))+(x_(2n−1−k) ^2 /(x−x_(2n−1−k) ))]}ByE⇒ =−(1/2){Σ_(k=0) ^(n−1) [(x_k ^2 /(x−x_k ))+(x_k ^(−2) /(x−x_k ^− ))]} =−(1/2)Σ_(k=0) ^(n−1) [((x(x_k ^2 +x_k ^(−2) )−x_k ^− x_k ^2 −x_k x_k ^(−2) )/(x^2 −2Re(x_k )x+∣x_k ∣^2 )) =−(1/2)Σ_(k=0) ^(n−1) ((2x(Re(x_k ^2 ))−2Re(x_k ))/(x^2 −2Re(x_k )+1)) =−(1/2)Σ_(k=0) ^(n−1) ((2x(cos(((1+2k)/n)π))−2cos(((1+2k)/(2n))π))/(x^2 −2cos(((1+2k)/(2n))π)+1)) over IR(x) ∫_0 ^(+∞) n(x^n /(x^(2n) +1))dx x=tg^(1/n) (t)⇒dx=(1/n)(1+tg^2 (t))tg^((1/n)−1) (t)dt =∫_0 ^(π/2) tg(t)(((1+tg^2 (t))tg^((1/n)−1) )/(1+tg^2 (t)))dt =∫_0 ^(π/2) tg^(1/n) (t)dt=∫_0 ^(π/2) sin^(1/n) (t)cos^(−(1/n)) (t)dt =(1/2)β(((1+n)/(2n)),((n−1)/(2n)))=(1/2).((Γ(((1+n)/(2n)))Γ(((n−1)/(2n))))/(Γ(((n+1)/(2n))+((n−1)/(2n)))))=((Γ(((n+1)/(2n))).Γ(1−((n+1)/(2n))))/(2Γ(1))) Γ(x)Γ(1−x)=(π/(sin(πx)))⇒Γ(((n+1)/(2n)))Γ(1−((n+1)/(2n)))=(π/(sin(((n+1)/(2n))π))),Γ(1)=1 =(π/(2sin(((n+1)/(2n))π)))=(π/(2cos((π/(2n)))))$
	$o v e r C (x)$ $x^{2 n} + 1 = 0 \Rightarrow x^{2 n} = - 1 = e^{i π + 2 k π}$ $x_{k} = e^{\frac{i (1 + 2 k) π}{2 n}}, k \in [0, 2 n - 1]$ $x_{2 n - k - 1} = e^{i (\frac{1 + 2 (2 n - k - 1)}{2 n}) π} = e^{- i (\frac{1 + 2 k}{2 n}) π}$ $\Rightarrow x_{k} = {\bar{x}}_{2 n - 1 - k}, E$ $\frac{{n x}^{n}}{x^{2 n} + 1} = Σ \frac{a_{k}}{x - x_{k}}$ $a_{k} = \frac{{n x}_{k}}{2 {n x}_{k}^{2 n - 1}} = \frac{1}{2 x_{k}^{2 n - 2}} = - \frac{x_{k}^{2}}{2}$ $\frac{{n x}^{n}}{x^{2 n} + 1} = - \frac{1}{2} \underset{k = 0}{\sum^{2 n - 1}} \frac{x_{k}^{2}}{(x - x_{k})}$ $o v e r R (X)$ $- \frac{1}{2} \underset{k = 0}{\sum^{2 n - 1}} \frac{x_{k}^{2}}{(x - x_{k})} = - \frac{1}{2} . {\underset{k = 0}{\sum^{n - 1}} \frac{x_{k}^{2}}{x - x_{k}} + \underset{k = n}{\sum^{2 n - 1}} \frac{x_{k}^{2}}{x - x_{k}}}$ $= - \frac{1}{2} {\underset{k = 0}{\sum^{n - 1}} [\frac{x_{k}^{2}}{x - x_{k}} + \frac{x_{2 n - 1 - k}^{2}}{x - x_{2 n - 1 - k}}]} B y E \Rightarrow$ $= - \frac{1}{2} {\underset{k = 0}{\sum^{n - 1}} [\frac{x_{k}^{2}}{x - x_{k}} + \frac{{\overset{- 2}{x}}_{k}}{x - {\bar{x}}_{k}}]}$ $= - \frac{1}{2} \underset{k = 0}{\sum^{n - 1}} [\frac{x (x_{k}^{2} + {\overset{- 2}{x}}_{k}) - {\bar{x}}_{k} x_{k}^{2} - x_{k} {\overset{- 2}{x}}_{k}}{x^{2} - 2 R e (x_{k}) x + ∣ x_{k} ∣^{2}}$ $= - \frac{1}{2} \underset{k = 0}{\sum^{n - 1}} \frac{2 x (R e (x_{k}^{2})) - 2 R e (x_{k})}{x^{2} - 2 R e (x_{k}) + 1}$ $= - \frac{1}{2} \underset{k = 0}{\sum^{n - 1}} \frac{2 x (c o s (\frac{1 + 2 k}{n} π)) - 2 c o s (\frac{1 + 2 k}{2 n} π)}{x^{2} - 2 c o s (\frac{1 + 2 k}{2 n} π) + 1} o v e r I R (x)$ $\int_{0}^{+ \infty} n \frac{x^{n}}{x^{2 n} + 1} d x$ $x = {t g}^{\frac{1}{n}} (t) \Rightarrow d x = \frac{1}{n} (1 + {t g}^{2} (t)) {t g}^{\frac{1}{n} - 1} (t) d t$ $= \int_{0}^{\frac{π}{2}} t g (t) \frac{(1 + {t g}^{2} (t)) {t g}^{\frac{1}{n} - 1}}{1 + {t g}^{2} (t)} d t$ $= \int_{0}^{\frac{π}{2}} {t g}^{\frac{1}{n}} (t) d t = \int_{0}^{\frac{π}{2}} {s i n}^{\frac{1}{n}} (t) {c o s}^{- \frac{1}{n}} (t) d t$ $= \frac{1}{2} β (\frac{1 + n}{2 n}, \frac{n - 1}{2 n}) = \frac{1}{2} . \frac{Γ (\frac{1 + n}{2 n}) Γ (\frac{n - 1}{2 n})}{Γ (\frac{n + 1}{2 n} + \frac{n - 1}{2 n})} = \frac{Γ (\frac{n + 1}{2 n}) . Γ (1 - \frac{n + 1}{2 n})}{2 Γ (1)}$ $Γ (x) Γ (1 - x) = \frac{π}{s i n (π x)} \Rightarrow Γ (\frac{n + 1}{2 n}) Γ (1 - \frac{n + 1}{2 n}) = \frac{π}{s i n (\frac{n + 1}{2 n} π)}, Γ (1) = 1$ $= \frac{π}{2 s i n (\frac{n + 1}{2 n} π)} = \frac{π}{2 c o s (\frac{π}{2 n})}$
	Commented by mathmax by abdo last updated on 23/Jan/20

	$t h a n k y o u s i r .$
	Commented by mind is power last updated on 23/Jan/20

	$y^{'} r e W e l c o m$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum