Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 7911 by ashis786 last updated on 24/Sep/16

If a>0, b>0, c>0 are respectively the p^(th) , q^(th) , r^(th) terms of a GP, then the value of the determinant determinant (((log a),p,1),((log b),q,1),((log c),r,1)) is

$$\mathrm{If}\:{a}>\mathrm{0},\:{b}>\mathrm{0},\:{c}>\mathrm{0}\:\mathrm{are}\:\mathrm{respectively}\:\mathrm{the} \\ $$ $${p}^{\mathrm{th}} ,\:{q}^{\mathrm{th}} ,\:{r}^{\mathrm{th}} \:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{GP},\:\mathrm{then}\:\mathrm{the}\:\mathrm{value} \\ $$ $$\mathrm{of}\:\mathrm{the}\:\mathrm{determinant}\:\begin{vmatrix}{\mathrm{log}\:{a}}&{{p}}&{\mathrm{1}}\\{\mathrm{log}\:{b}}&{{q}}&{\mathrm{1}}\\{\mathrm{log}\:{c}}&{{r}}&{\mathrm{1}}\end{vmatrix}\:\mathrm{is} \\ $$

Answered by prakash jain last updated on 24/Sep/16

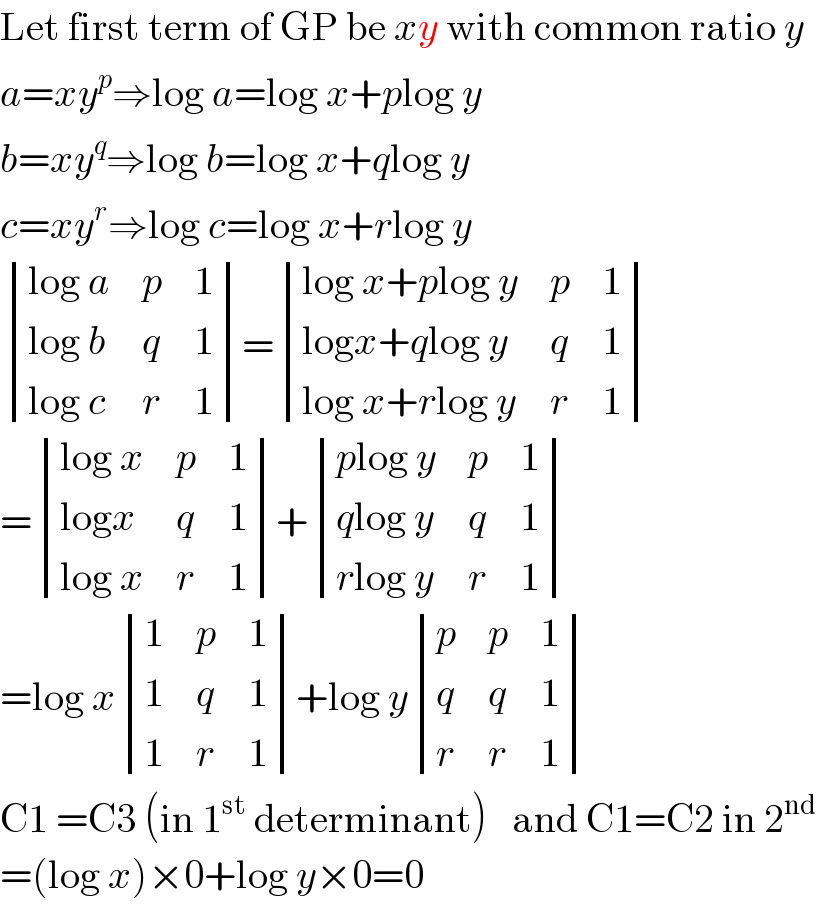
Let first term of GP be xy with common ratio y a=xy^p ⇒log a=log x+plog y b=xy^q ⇒log b=log x+qlog y c=xy^r ⇒log c=log x+rlog y determinant (((log a),p,1),((log b),q,1),((log c),r,1))= determinant (((log x+plog y),p,1),((logx+qlog y),q,1),((log x+rlog y),r,1)) = determinant (((log x),p,1),((logx),q,1),((log x),r,1))+ determinant (((plog y),p,1),((qlog y),q,1),((rlog y),r,1)) =log x determinant ((1,p,1),(1,q,1),(1,r,1))+log y determinant ((p,p,1),(q,q,1),(r,r,1)) C1 =C3 (in 1^(st) determinant) and C1=C2 in 2^(nd) =(log x)×0+log y×0=0

$$\mathrm{Let}\:\mathrm{first}\:\mathrm{term}\:\mathrm{of}\:\mathrm{GP}\:\mathrm{be}\:{xy}\:\mathrm{with}\:\mathrm{common}\:\mathrm{ratio}\:{y} \\ $$ $${a}={xy}^{{p}} \Rightarrow\mathrm{log}\:{a}=\mathrm{log}\:{x}+{p}\mathrm{log}\:{y} \\ $$ $${b}={xy}^{{q}} \Rightarrow\mathrm{log}\:{b}=\mathrm{log}\:{x}+{q}\mathrm{log}\:{y} \\ $$ $${c}={xy}^{{r}} \Rightarrow\mathrm{log}\:{c}=\mathrm{log}\:{x}+{r}\mathrm{log}\:{y} \\ $$ $$\begin{vmatrix}{\mathrm{log}\:{a}}&{{p}}&{\mathrm{1}}\\{\mathrm{log}\:{b}}&{{q}}&{\mathrm{1}}\\{\mathrm{log}\:{c}}&{{r}}&{\mathrm{1}}\end{vmatrix}=\begin{vmatrix}{\mathrm{log}\:{x}+{p}\mathrm{log}\:{y}}&{{p}}&{\mathrm{1}}\\{\mathrm{log}{x}+{q}\mathrm{log}\:{y}}&{{q}}&{\mathrm{1}}\\{\mathrm{log}\:{x}+{r}\mathrm{log}\:{y}}&{{r}}&{\mathrm{1}}\end{vmatrix} \\ $$ $$=\begin{vmatrix}{\mathrm{log}\:{x}}&{{p}}&{\mathrm{1}}\\{\mathrm{log}{x}}&{{q}}&{\mathrm{1}}\\{\mathrm{log}\:{x}}&{{r}}&{\mathrm{1}}\end{vmatrix}+\begin{vmatrix}{{p}\mathrm{log}\:{y}}&{{p}}&{\mathrm{1}}\\{{q}\mathrm{log}\:{y}}&{{q}}&{\mathrm{1}}\\{{r}\mathrm{log}\:{y}}&{{r}}&{\mathrm{1}}\end{vmatrix} \\ $$ $$=\mathrm{log}\:{x}\begin{vmatrix}{\mathrm{1}}&{{p}}&{\mathrm{1}}\\{\mathrm{1}}&{{q}}&{\mathrm{1}}\\{\mathrm{1}}&{{r}}&{\mathrm{1}}\end{vmatrix}+\mathrm{log}\:{y}\begin{vmatrix}{{p}}&{{p}}&{\mathrm{1}}\\{{q}}&{{q}}&{\mathrm{1}}\\{{r}}&{{r}}&{\mathrm{1}}\end{vmatrix} \\ $$ $$\mathrm{C1}\:=\mathrm{C3}\:\left(\mathrm{in}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{determinant}\right)\:\:\:\mathrm{and}\:\mathrm{C1}=\mathrm{C2}\:\mathrm{in}\:\mathrm{2}^{\mathrm{nd}} \\ $$ $$=\left(\mathrm{log}\:{x}\right)×\mathrm{0}+\mathrm{log}\:{y}×\mathrm{0}=\mathrm{0} \\ $$

Commented byRasheed Soomro last updated on 24/Sep/16

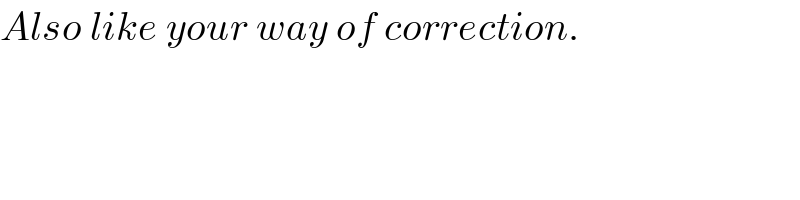
Also like your way of correction.

$${Also}\:{like}\:{your}\:{way}\:{of}\:{correction}.\:\:\: \\ $$

Commented byashis786 last updated on 24/Sep/16

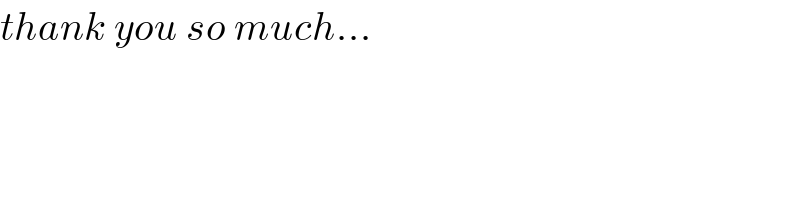
thank you so much...

$${thank}\:{you}\:{so}\:{much}... \\ $$

Commented bysandy_suhendra last updated on 24/Sep/16

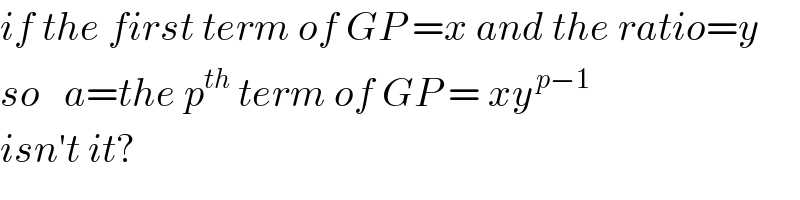
if the first term of GP =x and the ratio=y so a=the p^(th) term of GP = xy^( p−1) isn′t it?

$${if}\:{the}\:{first}\:{term}\:{of}\:{GP}\:={x}\:{and}\:{the}\:{ratio}={y} \\ $$ $${so}\:\:\:{a}={the}\:{p}^{{th}} \:{term}\:{of}\:{GP}\:=\:{xy}^{\:{p}−\mathrm{1}} \: \\ $$ $${isn}'{t}\:{it}? \\ $$

Commented byprakash jain last updated on 24/Sep/16

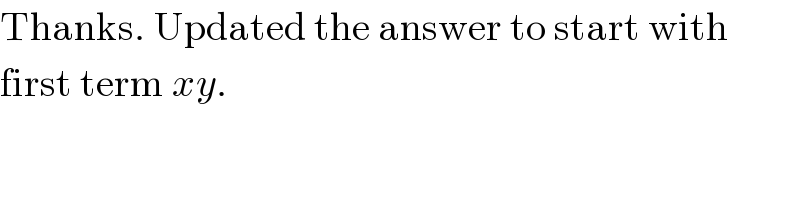
Thanks. Updated the answer to start with first term xy.

$$\mathrm{Thanks}.\:\mathrm{Updated}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{start}\:\mathrm{with} \\ $$ $$\mathrm{first}\:\mathrm{term}\:{xy}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com