Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 79126 by ~blr237~ last updated on 22/Jan/20

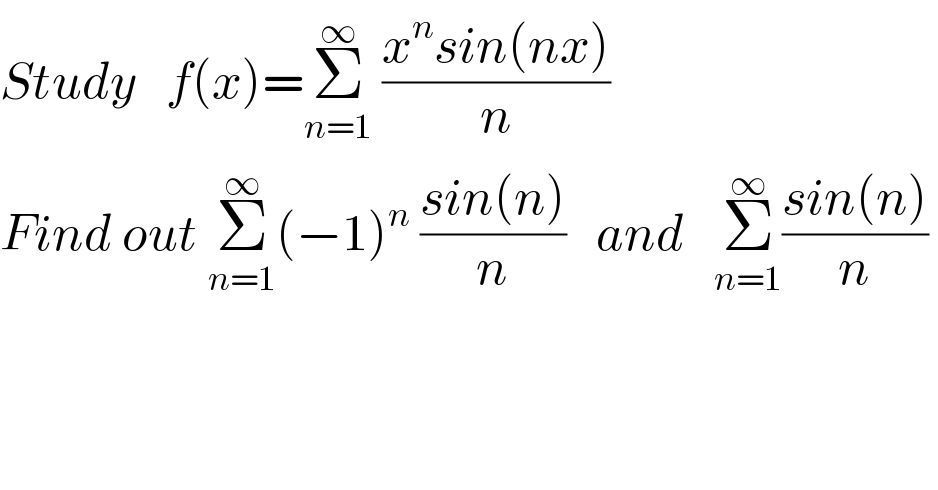
Study f(x)=Σ_(n=1) ^∞ ((x^n sin(nx))/n) Find out Σ_(n=1) ^∞ (−1)^n ((sin(n))/n) and Σ_(n=1) ^∞ ((sin(n))/n)

$${Study}\:\:\:{f}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}} {sin}\left({nx}\right)}{{n}} \\ $$$${Find}\:{out}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \:\frac{{sin}\left({n}\right)}{{n}}\:\:\:{and}\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left({n}\right)}{{n}}\: \\ $$

Commented by mathmax by abdo last updated on 25/Jan/20

let s(x)=Σ_(n=1) ^∞ ((sin(nx))/n) we have s(x)=Im(Σ_(n=1) ^∞ (e^(inx) /n)) let w(x)=Σ_(n=1) ^∞ (e^(inx) /n) ⇒w^′ (x)=Σ_(n=1) ^∞ ((in e^(inx) )/n) =i Σ_(n=1) ^∞ (e^(ix) )^n =i{ Σ_(n=0) ^∞ (e^(ix) )^n −1} =i{(1/(1−e^(ix) ))−1} =i{ (1/(1−cosx −isinx))−1} =i{((1−cosx +isinx)/((1−cosx)^2 +sin^2 x))−1} =i(((1−cosx)/((1−cosx)^2 +sin^2 x)))−((sinx)/((1−cosx)^2 +sin^2 x))−i =i(((1−cosx)/(2−2cosx))−1)−((sinx)/(2−2cosx)) =−(i/2)−((sinx)/(4sin^2 ((x/2)))) =−(i/2)−((cos((x/2)))/(2sin((x/2)))) ⇒w(x)=−((ix)/2)−(1/2)∫((cos((x/2)))/(sin((x/2))))dx+c ((x/2)=t) w(x)=−((ix)/2)−∫ ((cost)/(sint))dt =−i(x/2)−ln∣sin((x/2))∣+c w(π)=Σ_(n=1) ^∞ (((−1)^n )/n) =−ln(2)=−((iπ)/2) +c ⇒c =−ln(2)+((iπ)/2) ⇒ w(x)=−((ix)/2)−ln∣sin((x/2))∣−ln(2)+((iπ)/2) =−ln(2 sin((x/2))∣+i((π−x)/2) Im(w(x) =((π−x)/2) =s(x) x=1 ⇒Σ_(n=1) ^∞ ((sin(n))/n) =((π−1)/2)

$${let}\:{s}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{n}}\:\:\:\:\:\:{we}\:{have}\:{s}\left({x}\right)={Im}\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{inx}} }{{n}}\right) \\ $$$${let}\:{w}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{inx}} }{{n}}\:\Rightarrow{w}^{'} \left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{in}\:{e}^{{inx}} }{{n}} \\ $$$$={i}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left({e}^{{ix}} \right)^{{n}} \:={i}\left\{\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left({e}^{{ix}} \right)^{{n}} −\mathrm{1}\right\} \\ $$$$={i}\left\{\frac{\mathrm{1}}{\mathrm{1}−{e}^{{ix}} }−\mathrm{1}\right\}\:={i}\left\{\:\frac{\mathrm{1}}{\mathrm{1}−{cosx}\:−{isinx}}−\mathrm{1}\right\} \\ $$$$={i}\left\{\frac{\mathrm{1}−{cosx}\:+{isinx}}{\left(\mathrm{1}−{cosx}\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} {x}}−\mathrm{1}\right\}\:={i}\left(\frac{\mathrm{1}−{cosx}}{\left(\mathrm{1}−{cosx}\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} {x}}\right)−\frac{{sinx}}{\left(\mathrm{1}−{cosx}\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} {x}}−{i} \\ $$$$={i}\left(\frac{\mathrm{1}−{cosx}}{\mathrm{2}−\mathrm{2}{cosx}}−\mathrm{1}\right)−\frac{{sinx}}{\mathrm{2}−\mathrm{2}{cosx}}\:=−\frac{{i}}{\mathrm{2}}−\frac{{sinx}}{\mathrm{4}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=−\frac{{i}}{\mathrm{2}}−\frac{{cos}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\:\Rightarrow{w}\left({x}\right)=−\frac{{ix}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{cos}\left(\frac{{x}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}{dx}+{c}\:\:\left(\frac{{x}}{\mathrm{2}}={t}\right) \\ $$$${w}\left({x}\right)=−\frac{{ix}}{\mathrm{2}}−\int\:\:\frac{{cost}}{{sint}}{dt}\:=−{i}\frac{{x}}{\mathrm{2}}−{ln}\mid{sin}\left(\frac{{x}}{\mathrm{2}}\right)\mid+{c} \\ $$$${w}\left(\pi\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:=−{ln}\left(\mathrm{2}\right)=−\frac{{i}\pi}{\mathrm{2}}\:+{c}\:\Rightarrow{c}\:=−{ln}\left(\mathrm{2}\right)+\frac{{i}\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${w}\left({x}\right)=−\frac{{ix}}{\mathrm{2}}−{ln}\mid{sin}\left(\frac{{x}}{\mathrm{2}}\right)\mid−{ln}\left(\mathrm{2}\right)+\frac{{i}\pi}{\mathrm{2}}\:=−{ln}\left(\mathrm{2}\:{sin}\left(\frac{{x}}{\mathrm{2}}\right)\mid+{i}\frac{\pi−{x}}{\mathrm{2}}\right. \\ $$$${Im}\left({w}\left({x}\right)\:=\frac{\pi−{x}}{\mathrm{2}}\:={s}\left({x}\right)\right. \\ $$$${x}=\mathrm{1}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({n}\right)}{{n}}\:=\frac{\pi−\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 25/Jan/20

f(x)=Im(Σ_(n=1) ^∞ ((e^(inx) x^n )/n)) let ϕ(x)=Σ_(n=1) ^∞ ((e^(inx) x^n )/n) ⇒ϕ(x)=Σ_(n=1) ^∞ (((xe^(ix) )^n )/n) =Σ_(n=1) ^∞ (z^n /n) with z =x e^(ix) for ∣z∣=∣x∣≤ wr get (d/dz)(Σ (z^n /n)) =Σ_(n=1) ^∞ z^(n−1) =Σ_(n=0) ^∞ z^n =(1/(1−z)) ⇒Σ_(n=1) ^∞ (z^n /n) =−ln(1−z) −ln(1−xe^(ix) ) =−ln(1−x(cosx +isinx)) =−ln(1−xcosx −ixsinx) we hsve ∣1−xcosx−ixsinx∣ =(√((1−xcosx)^2 +x^2 sin^2 x)) =(√(1−2xcosx +x^2 )) ⇒1−xcosx −ixsinx =(√(x^2 −2x cosx +1))e^(isrctan(((−xsinx)/(1−xcosx)))) ⇒ −ln(...) =−(1/2)ln(x^2 −2x cosx +1)+i arctan(((xsinx)/(1−xcosx))) f(x) =Im(ϕ(x)) =arctan(((xsinx)/(1−x cosx))) x=−1 ⇒Σ_(n=1) ^∞ (((−1)^n )/n)sin(n) =arctan(((sin(1))/(1+cos(1)))) =arctan(((2sin((1/2))cos((1/2)))/(2cos^2 ((1/2))))) =(1/2)

$${f}\left({x}\right)={Im}\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{inx}} \:{x}^{{n}} }{{n}}\right)\:{let}\: \\ $$$$\varphi\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{inx}} \:{x}^{{n}} }{{n}}\:\Rightarrow\varphi\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left({xe}^{{ix}} \right)^{{n}} }{{n}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}} }{{n}} \\ $$$${with}\:{z}\:={x}\:{e}^{{ix}} \:\:\:{for}\:\mid{z}\mid=\mid{x}\mid\leqslant\:\:{wr}\:{get} \\ $$$$\frac{{d}}{{dz}}\left(\Sigma\:\frac{{z}^{{n}} }{{n}}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{z}^{{n}−\mathrm{1}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:{z}^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−{z}}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}} }{{n}}\:=−{ln}\left(\mathrm{1}−{z}\right) \\ $$$$−{ln}\left(\mathrm{1}−{xe}^{{ix}} \right)\:=−{ln}\left(\mathrm{1}−{x}\left({cosx}\:+{isinx}\right)\right) \\ $$$$=−{ln}\left(\mathrm{1}−{xcosx}\:−{ixsinx}\right)\:\:{we}\:{hsve} \\ $$$$\mid\mathrm{1}−{xcosx}−{ixsinx}\mid\:=\sqrt{\left(\mathrm{1}−{xcosx}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} \:{sin}^{\mathrm{2}} {x}} \\ $$$$=\sqrt{\mathrm{1}−\mathrm{2}{xcosx}\:+{x}^{\mathrm{2}} \:}\:\Rightarrow\mathrm{1}−{xcosx}\:−{ixsinx} \\ $$$$=\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}\:{cosx}\:+\mathrm{1}}{e}^{{isrctan}\left(\frac{−{xsinx}}{\mathrm{1}−{xcosx}}\right)} \:\Rightarrow \\ $$$$−{ln}\left(...\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\:{cosx}\:+\mathrm{1}\right)+{i}\:{arctan}\left(\frac{{xsinx}}{\mathrm{1}−{xcosx}}\right) \\ $$$${f}\left({x}\right)\:={Im}\left(\varphi\left({x}\right)\right)\:={arctan}\left(\frac{{xsinx}}{\mathrm{1}−{x}\:{cosx}}\right) \\ $$$${x}=−\mathrm{1}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}{sin}\left({n}\right)\:={arctan}\left(\frac{{sin}\left(\mathrm{1}\right)}{\mathrm{1}+{cos}\left(\mathrm{1}\right)}\right) \\ $$$$={arctan}\left(\frac{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$

Answered by mind is power last updated on 23/Jan/20

if ∣x∣>1 lim_(n→∞) ((x^n sin(nx))/n),did′nt existe ⇒x∈[−1,1] x=1 we use abel lemma since (1/n) decrease in zero Σ_(n≥1) sin(n)=ImΣ_(N≥n≥1) e^(in) =Ime^i (((1−e^(i(N+1)) )/(1−e^i ))) =Im(e^(i/2) (((e^(i((N+1)/2)) sin(((N+1)/2)))/(sin((1/2)))))) =((sin(((N+2)/2))sin(((N+1)/2)))/(sin((1/2))))⇒∣Σsin(n)∣≤(1/(∣sin((1/2))∣)) by abel Σ_(n≥1) ((sin(n))/n) cv for −1, Σ_(n≥1) (((−1)^n sin(n))/n) sam ∣Σ(−1)^n sin(n)∣<∞,(1/n) decrease →0 cv for x∈[−a,a] ,0≤a<1 f(x)≤Σ_(n≥1) ((∣x∣^n )/n)=−ln(1−∣x∣) evident f is well defind in [−1,1] f(x)=Σ((x^n sin(n))/n)=Σ(x^n /n)Im(e^(in) ) =ImΣ((x^n e^(in) )/n)=ImΣ(((xe^i )^n )/n)=Im{−ln(1−xe^i )} =Im{−ln(1−xcos(1)−ixsin(1)) 1−xcos(1)−ixsin(1)=(√(1+x^2 −2xcos(1)))e^(i(arctan(((−xsin(1))/(1−xcos(1))))) ln(1−xe^i )=ln((√(1+x^2 −2xcos(1))))+i(arctan(((−xsin(1))/(1−xcos(1))))) Im{−ln(1−xe^i )}=−arctan(((−xsin(1))/(1−xcos(1))))=arctan(((xsin(1))/(1−xcos(1)))) f(1)=Σ_(n≥1) ((sin(n))/n)=arctan(((sin(1))/(1−cos(1))))=arctan(((2sin((1/2))cos((1/2)))/(2sin^2 ((1/2))))) =arctan(tan((π/2)−(1/2)))=((π−1)/2) f(−1)=Σ_(n≥1) (((−1)^n sin(n))/n)=arctan(((−sin(1))/(1+cos(1))))=−arctan(tg((1/2))) =−(1/2)

$${if}\:\mid{x}\mid>\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{{n}} {sin}\left({nx}\right)}{{n}},{did}'{nt}\:{existe} \\ $$$$\Rightarrow{x}\in\left[−\mathrm{1},\mathrm{1}\right] \\ $$$${x}=\mathrm{1}\:\:{we}\:{use}\:{abel}\:{lemma} \\ $$$${since}\:\frac{\mathrm{1}}{{n}}\:{decrease}\:{in}\:{zero} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}{sin}\left({n}\right)={Im}\underset{{N}\geqslant{n}\geqslant\mathrm{1}} {\sum}{e}^{{in}} ={Ime}^{{i}} \left(\frac{\mathrm{1}−{e}^{{i}\left({N}+\mathrm{1}\right)} }{\mathrm{1}−{e}^{{i}} }\right) \\ $$$$={Im}\left({e}^{\frac{{i}}{\mathrm{2}}} \left(\frac{{e}^{{i}\frac{{N}+\mathrm{1}}{\mathrm{2}}} {sin}\left(\frac{{N}+\mathrm{1}}{\mathrm{2}}\right)}{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\right)\right) \\ $$$$=\frac{{sin}\left(\frac{{N}+\mathrm{2}}{\mathrm{2}}\right){sin}\left(\frac{{N}+\mathrm{1}}{\mathrm{2}}\right)}{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\Rightarrow\mid\Sigma{sin}\left({n}\right)\mid\leqslant\frac{\mathrm{1}}{\mid{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mid} \\ $$$${by}\:{abel}\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left({n}\right)}{{n}}\:\:{cv} \\ $$$${for}\:−\mathrm{1},\:\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left({n}\right)}{{n}} \\ $$$${sam}\:\mid\Sigma\left(−\mathrm{1}\right)^{{n}} {sin}\left({n}\right)\mid<\infty,\frac{\mathrm{1}}{{n}}\:{decrease}\:\rightarrow\mathrm{0}\:\:{cv} \\ $$$${for}\:{x}\in\left[−{a},{a}\right]\:\:,\mathrm{0}\leqslant{a}<\mathrm{1} \\ $$$${f}\left({x}\right)\leqslant\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mid{x}\mid^{{n}} }{{n}}=−{ln}\left(\mathrm{1}−\mid{x}\mid\right)\:\:{evident}\:\: \\ $$$${f}\:{is}\:{well}\:{defind}\:{in}\:\left[−\mathrm{1},\mathrm{1}\right] \\ $$$${f}\left({x}\right)=\Sigma\frac{{x}^{{n}} {sin}\left({n}\right)}{{n}}=\Sigma\frac{{x}^{{n}} }{{n}}{Im}\left({e}^{{in}} \right) \\ $$$$={Im}\Sigma\frac{{x}^{{n}} {e}^{{in}} }{{n}}={Im}\Sigma\frac{\left({xe}^{{i}} \right)^{{n}} }{{n}}={Im}\left\{−{ln}\left(\mathrm{1}−{xe}^{{i}} \right)\right\} \\ $$$$={Im}\left\{−{ln}\left(\mathrm{1}−{xcos}\left(\mathrm{1}\right)−{ixsin}\left(\mathrm{1}\right)\right)\right. \\ $$$$\mathrm{1}−{xcos}\left(\mathrm{1}\right)−{ixsin}\left(\mathrm{1}\right)=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{xcos}\left(\mathrm{1}\right)}{e}^{{i}\left({arctan}\left(\frac{−{xsin}\left(\mathrm{1}\right)}{\mathrm{1}−{xcos}\left(\mathrm{1}\right)}\right)\right.} \\ $$$${ln}\left(\mathrm{1}−{xe}^{{i}} \right)={ln}\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{xcos}\left(\mathrm{1}\right)}\right)+{i}\left({arctan}\left(\frac{−{xsin}\left(\mathrm{1}\right)}{\mathrm{1}−{xcos}\left(\mathrm{1}\right)}\right)\right) \\ $$$${Im}\left\{−{ln}\left(\mathrm{1}−{xe}^{{i}} \right)\right\}=−{arctan}\left(\frac{−{xsin}\left(\mathrm{1}\right)}{\mathrm{1}−{xcos}\left(\mathrm{1}\right)}\right)={arctan}\left(\frac{{xsin}\left(\mathrm{1}\right)}{\mathrm{1}−{xcos}\left(\mathrm{1}\right)}\right) \\ $$$${f}\left(\mathrm{1}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left({n}\right)}{{n}}={arctan}\left(\frac{{sin}\left(\mathrm{1}\right)}{\mathrm{1}−{cos}\left(\mathrm{1}\right)}\right)={arctan}\left(\frac{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\right) \\ $$$$={arctan}\left({tan}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=\frac{\pi−\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left(−\mathrm{1}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {sin}\left({n}\right)}{{n}}={arctan}\left(\frac{−{sin}\left(\mathrm{1}\right)}{\mathrm{1}+{cos}\left(\mathrm{1}\right)}\right)=−{arctan}\left({tg}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com