Question Number 79377 by mr W last updated on 24/Jan/20
Commented by mr W last updated on 24/Jan/20
$${the}\:{side}\:{length}\:{of}\:{the}\:{square}\:{is}\:{a}. \\ $$$${find}\:{the}\:{radius}\:{of}\:{the}\:{n}−{th}\:{small} \\ $$$${circle}\:{r}_{{n}} . \\ $$
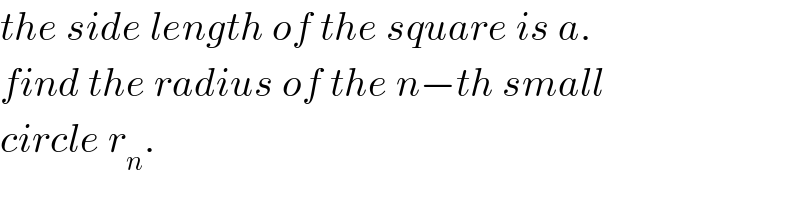
Commented by key of knowledge last updated on 24/Jan/20
$$\mathrm{mr}\:\mathrm{w}\:\mathrm{you}\:\mathrm{like}\:\mathrm{this}\:\mathrm{problem}! \\ $$
Commented by mr W last updated on 24/Jan/20
$${yes}\:{sir}.\:{i}\:{try}\:{to}\:{learn}\:{some}\:{new}\:{things}\: \\ $$$${through}\:{this}\:{problem}. \\ $$
Answered by mr W last updated on 25/Jan/20
$${we}\:{have}\:{got}\:{r}_{\mathrm{0}} =\frac{{a}}{\mathrm{3}}\:\left({vertical}\:{semicircle}\right) \\ $$$${if}\:{we}\:{know}\:{r}_{{n}} ,\:{how}\:{can}\:{we}\:{get}\:{r}_{{n}+\mathrm{1}} ? \\ $$$${we}\:{can}\:{apply}\:{the}\:{Descartes}'\:{theorem} \\ $$$${as}\:{following}: \\ $$$$\left(−\frac{\mathrm{1}}{{a}}+\frac{\mathrm{2}}{{a}}+\frac{\mathrm{1}}{{r}_{{n}} }+\frac{\mathrm{1}}{{r}_{{n}+\mathrm{1}} }\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{4}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{{n}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{{n}+\mathrm{1}} ^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{2}}{{ar}_{{n}} }+\frac{\mathrm{2}}{{ar}_{{n}+\mathrm{1}} }+\frac{\mathrm{2}}{{r}_{{n}} {r}_{{n}+\mathrm{1}} }=\frac{\mathrm{9}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{{n}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{{n}+\mathrm{1}} ^{\mathrm{2}} } \\ $$$$\left(\frac{{a}}{{r}_{{n}+\mathrm{1}} }−\frac{{a}}{{r}_{{n}} }\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{a}}{{r}_{{n}+\mathrm{1}} }−\frac{{a}}{{r}_{{n}} }\right)+\mathrm{9}−\mathrm{4}\frac{{a}}{{r}_{{n}} }=\mathrm{0} \\ $$$$\Rightarrow\frac{{a}}{{r}_{{n}+\mathrm{1}} }−\frac{{a}}{{r}_{{n}} }=\mathrm{1}+\mathrm{2}\sqrt{\frac{{a}}{{r}_{{n}} }−\mathrm{2}} \\ $$$$\Rightarrow\frac{{a}}{{r}_{{n}+\mathrm{1}} }=\frac{{a}}{{r}_{{n}} }+\mathrm{2}\sqrt{\frac{{a}}{{r}_{{n}} }−\mathrm{2}}+\mathrm{1} \\ $$$$\frac{{a}}{{r}_{\mathrm{0}} }=\mathrm{3} \\ $$$$\frac{{a}}{{r}_{{n}+\mathrm{1}} }−\mathrm{2}=\frac{{a}}{{r}_{{n}} }−\mathrm{2}+\mathrm{2}\sqrt{\frac{{a}}{{r}_{{n}} }−\mathrm{2}}+\mathrm{1} \\ $$$$\frac{{a}}{{r}_{{n}+\mathrm{1}} }−\mathrm{2}=\left(\sqrt{\frac{{a}}{{r}_{{n}} }−\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${let}\:{b}_{{n}} =\sqrt{\frac{{a}}{{r}_{{n}} }−\mathrm{2}} \\ $$$$\Rightarrow{b}_{{n}+\mathrm{1}} ^{\mathrm{2}} =\left({b}_{{n}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{b}_{{n}+\mathrm{1}} ={b}_{{n}} +\mathrm{1}\:\:\:\Rightarrow\:{it}'{s}\:{a}\:{A}.{P}.\:! \\ $$$$\Rightarrow{b}_{{n}} ={b}_{\mathrm{0}} +{n} \\ $$$${b}_{\mathrm{0}} =\sqrt{\frac{{a}}{{r}_{\mathrm{0}} }−\mathrm{2}}=\sqrt{\mathrm{3}−\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow{b}_{{n}} ={n}+\mathrm{1} \\ $$$$\Rightarrow\sqrt{\frac{{a}}{{r}_{{n}} }−\mathrm{2}}={n}+\mathrm{1} \\ $$$$\Rightarrow\frac{{a}}{{r}_{{n}} }=\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2} \\ $$$$\Rightarrow{r}_{{n}} =\frac{{a}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 25/Jan/20
![great! dear master. can you applay this method to:Q#10455 (and also meet a nostalgia!) [nostos:return to home algia:be in suffer]](Q79428.png)
$$\mathrm{great}!\:\mathrm{dear}\:\mathrm{master}. \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{applay}\:\mathrm{this}\:\mathrm{method}\:\mathrm{to}:\mathrm{Q}#\mathrm{10455} \\ $$$$\left(\mathrm{and}\:\mathrm{also}\:\mathrm{meet}\:\mathrm{a}\:\mathrm{nostalgia}!\right) \\ $$$$\left[\mathrm{nostos}:\mathrm{return}\:\mathrm{to}\:\mathrm{home}\right. \\ $$$$\left.\mathrm{algia}:\mathrm{be}\:\mathrm{in}\:\mathrm{suffer}\right] \\ $$
Commented by mr W last updated on 25/Jan/20
$${haha},\:{you}\:{still}\:{remember}\:{that}\:{oldie}! \\ $$$${let}\:{me}\:{try}\:{if}\:{it}\:{could}\:{be}\:{solved}\:{in} \\ $$$${similary}\:{way}. \\ $$
Commented by behi83417@gmail.com last updated on 25/Jan/20
$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{dear}\:\mathrm{master}. \\ $$