
Question and Answers Forum
Question Number 79449 by mr W last updated on 25/Jan/20
Commented by mr W last updated on 25/Jan/20
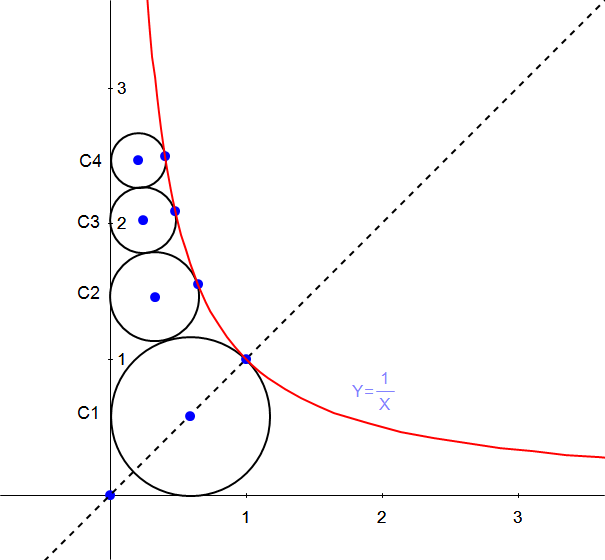
![[Repost of an old question from b.e.h.i. sir] Find the radius of 20th circle.](Q79450.png)
Commented by MJS last updated on 25/Jan/20
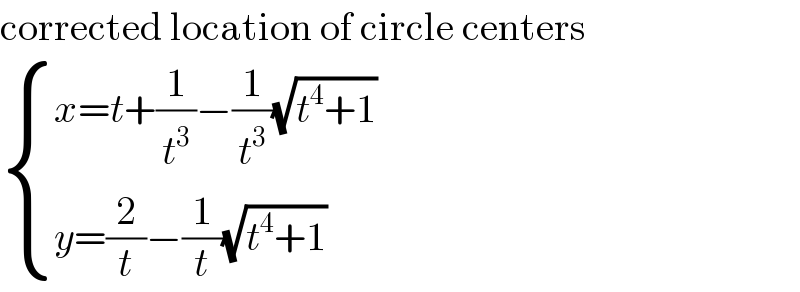
Commented by john santu last updated on 25/Jan/20

Commented by MJS last updated on 25/Jan/20
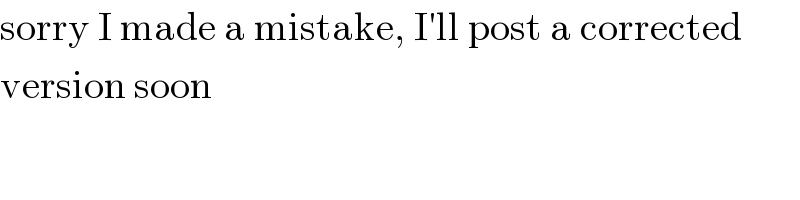
Commented by MJS last updated on 25/Jan/20
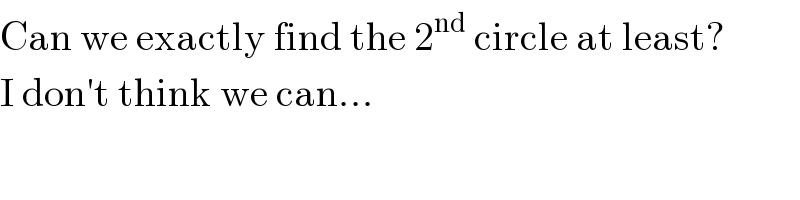
Commented by MJS last updated on 25/Jan/20
![one possible path, but no exact solution center of C_n =M_n = (((t_n +(1/t_n ^3 )−(1/t_n ^3 )(√(t_n ^4 +1)))),(((2/t_n )−(1/t_n )(√(t_n ^4 +1)))) ) radius of C_n =r_n =t_n +(1/t_n ^3 )−(1/t_n ^3 )(√(t_n ^4 +1)) [t_1 =1 ⇒ M_1 = (((2−(√2))),((2−(√2))) ) ∧ r_1 =2−(√2)] ∣C_n C_(n+1) ∣^2 =(r_n +r_(n+1) )^2 starting with n=1 let t_2 =p (((4−2(√2))/p)−(6/p^2 )+((4−2(√2))/p^3 )−(2/p^6 ))(√(p^4 +1))+2p^2 −(4−2(√2))p−((8−4(√2))/p)+(8/p^2 )−((4−2(√2))/p^3 )+(2/p^6 )+12−8(√2)=+((2/p^2 )+((4−2(√2))/p^3 )+(2/p^6 ))(√(p^4 +1))+p^2 +(4−2(√2))p+(3/p^2 )+((4−2(√2))/p^3 )+(2/p^6 )+6−4]2 ... p(p−1)^2 (p^7 −2(7−4(√2))p^6 +5(11−8(√2))p^5 −4(5−4(√2))p^4 +(63−40(√2))p^3 −2(23−16(√2))p^3 +(73−48(√2))p−8(2−(√2)))=0 we know p≠0∧p≠1 we′re looking for 0<p<1 (there are several possible circles, touching C_1 from “wrong sides”) ⇒ p≈.631658=t_2 ⇒ r_2 ≈.327488 of course we can go on like this but I guess if I calculate with an error of ±10^(−14) at least t_(14) will have an error of ±1 ...](Q79514.png)
Answered by mr W last updated on 25/Jan/20
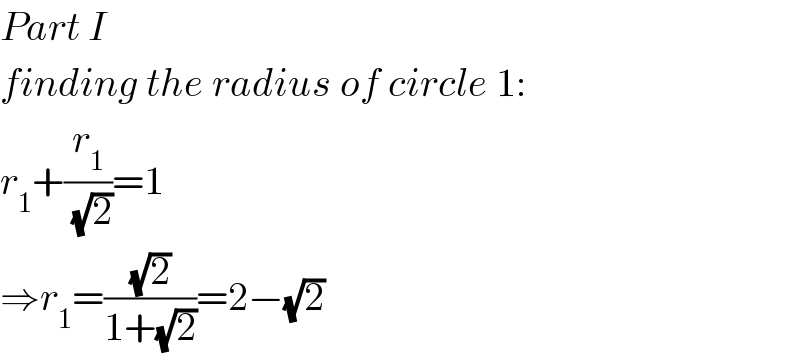
Commented by mr W last updated on 25/Jan/20
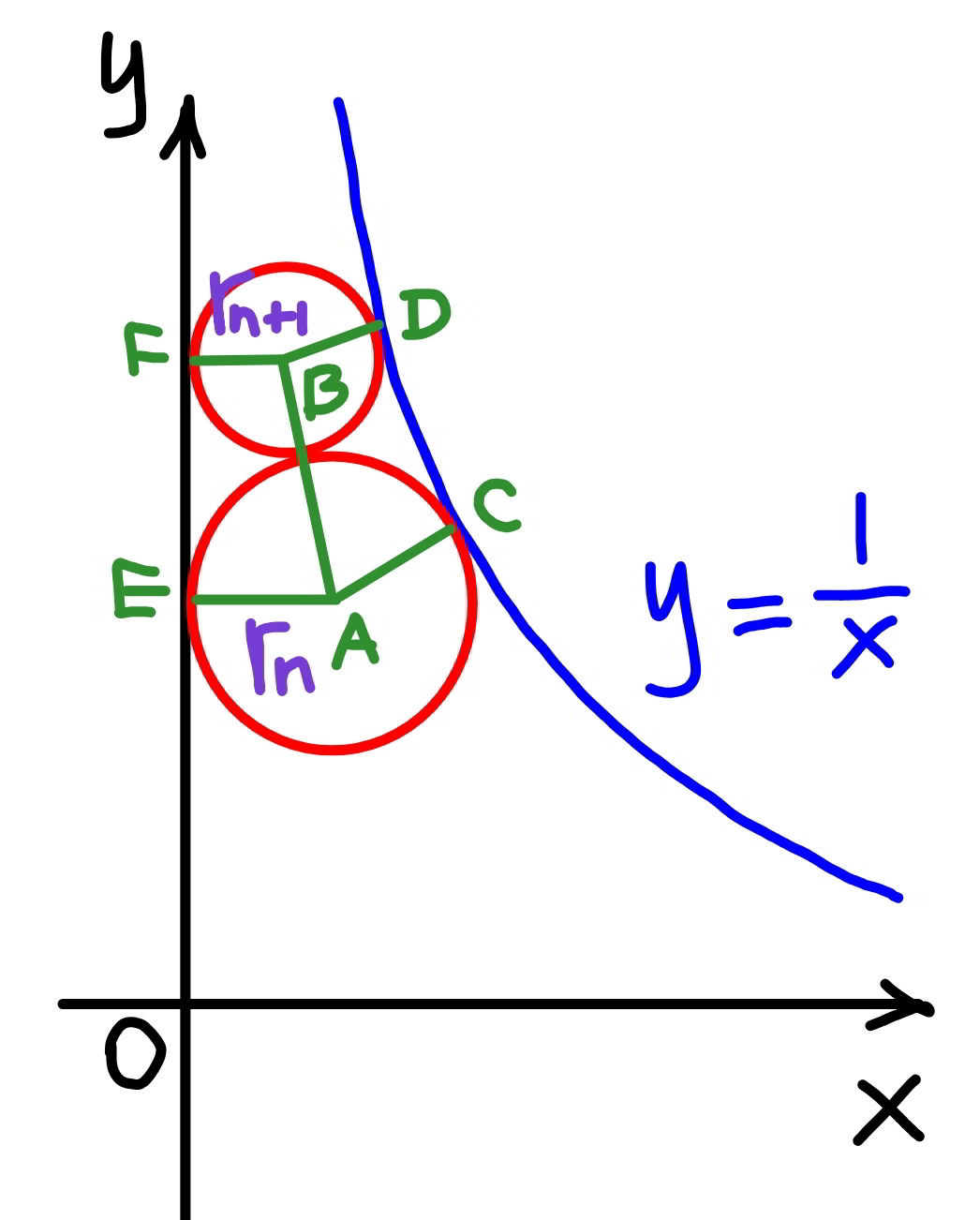
Commented by mr W last updated on 25/Jan/20

Commented by behi83417@gmail.com last updated on 25/Jan/20

Commented by behi83417@gmail.com last updated on 25/Jan/20
![x_c ^3 .r_n ^2 −2(1+x_c ^4 )r_n +x_c ^5 +x_c =0 r_n =((1+x_c ^4 ±(√((1+x_c ^4 )^2 −x_c ^3 (x_c ^5 +x_c ))))/x_c ^3 ) ⇒r_n = { (((1+x_c ^4 +(√(1+x_c ^4 )))/x_c ^3 )),(((1+x_c ^4 −(√(1+x_c ^4 )))/x_c ^3 )) :} ⇒^(x_c =x) (∂r_n /∂x_c )=(((4x^3 +((2x^3 )/(√(1+x^4 ))))x^3 −3x^2 (1+x^4 +(√(1+x^4 ))))/x^6 )=0 ⇒x^2 [4x^4 (√(1+x^4 ))+2x^3 )−3(1+x^4 +(1+x^4 )(√(1+x^4 )))]=0 ⇒ { (,(x=0 [not ok])),(,(4x^4 (√(1+x^4 ))+2x^3 −3−3x^4 −3(√(1+x^4 ))−3x^4 (√(1+x^4 ))=0)) :} ⇒(√(1+x^4 ))(x^4 −3)=3x^4 −2x^3 +3 ⇒(1+x^4 )(x^8 −6x^4 +9)=9x^8 +4x^6 +9−12x^7 +18x^4 −12x^3 ⇒x^(12) −5x^8 +3x^4 +9=9x^8 −12x^7 +4x^6 +18x^4 −12x^3 ⇒x^(12) −14x^8 +12x^7 −4x^6 −15x^4 +12x^3 =0 ⇒ { ((x^3 =0[not ok])),((x^9 −14x^5 +12x^4 −4x^3 −15x+12=0)) :} ⇒x=−2.51 ,0.733 ,1.747 ⇒r_n =((1+1.747^4 +(√(1+1.747^4 )))/(1.747^3 ))=2.537(×) ⇒r_n =((1+.733^4 +(√(1+.733^4 )))/(0.733^3 ))=6.155 (×) ⇒r_n =((1+(−2.51)^4 +(√(1+(−2.51)^4 )))/((−2.51)^3 ))=−2.97(×)](Q79483.png)
