Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 7945 by Rasheed Soomro last updated on 25/Sep/16

Commented by Rasheed Soomro last updated on 25/Sep/16

In above figure AF ,a diameter of the circle with centre G has been trisected at B & D (i-e AB=BD=DF) Is there any point H on the circle for which ∠AHB=∠BHD=∠DHF I-E β=γ=δ ? If yes then what is ∠HGF?

$${In}\:{above}\:{figure}\:{AF}\:,{a}\:{diameter}\:{of}\:{the} \\ $$$${circle}\:{with}\:{centre}\:{G}\:{has}\:{been}\:{trisected} \\ $$$${at}\:{B}\:\&\:{D}\:\left({i}-{e}\:{AB}={BD}={DF}\right) \\ $$$${Is}\:{there}\:{any}\:{point}\:{H}\:{on}\:{the}\:{circle}\:{for} \\ $$$${which}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\angle{AHB}=\angle{BHD}=\angle{DHF} \\ $$$${I}-\mathcal{E}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\beta=\gamma=\delta\:\:\:\:\:? \\ $$$${If}\:\:\:{yes}\:{then}\:{what}\:{is}\:\angle{HGF}? \\ $$

Commented by prakash jain last updated on 27/Sep/16

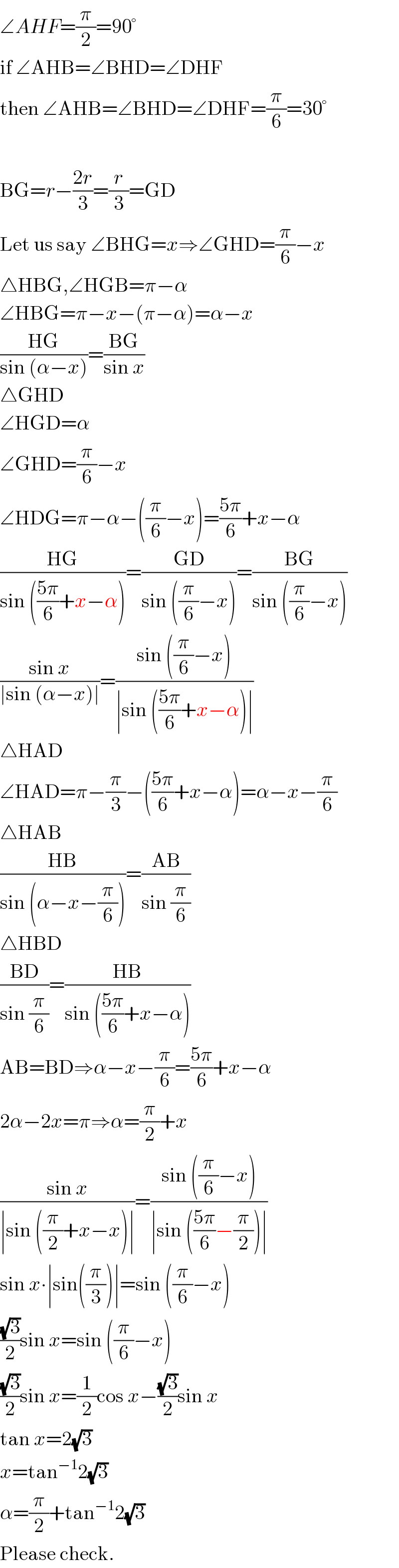
∠AHF=(π/2)=90° if ∠AHB=∠BHD=∠DHF then ∠AHB=∠BHD=∠DHF=(π/6)=30° BG=r−((2r)/3)=(r/3)=GD Let us say ∠BHG=x⇒∠GHD=(π/6)−x △HBG,∠HGB=π−α ∠HBG=π−x−(π−α)=α−x ((HG)/(sin (α−x)))=((BG)/(sin x)) △GHD ∠HGD=α ∠GHD=(π/6)−x ∠HDG=π−α−((π/6)−x)=((5π)/6)+x−α ((HG)/(sin (((5π)/6)+x−α)))=((GD)/(sin ((π/6)−x)))=((BG)/(sin ((π/6)−x))) ((sin x)/(∣sin (α−x)∣))=((sin ((π/6)−x))/(∣sin (((5π)/6)+x−α)∣)) △HAD ∠HAD=π−(π/3)−(((5π)/6)+x−α)=α−x−(π/6) △HAB ((HB)/(sin (α−x−(π/6))))=((AB)/(sin (π/6))) △HBD ((BD)/(sin (π/6)))=((HB)/(sin (((5π)/6)+x−α))) AB=BD⇒α−x−(π/6)=((5π)/6)+x−α 2α−2x=π⇒α=(π/2)+x ((sin x)/(∣sin ((π/2)+x−x)∣))=((sin ((π/6)−x))/(∣sin (((5π)/6)−(π/2))∣)) sin x∙∣sin((π/3))∣=sin ((π/6)−x) ((√3)/2)sin x=sin ((π/6)−x) ((√3)/2)sin x=(1/2)cos x−((√3)/2)sin x tan x=2(√3) x=tan^(−1) 2(√3) α=(π/2)+tan^(−1) 2(√3) Please check.

$$\angle{AHF}=\frac{\pi}{\mathrm{2}}=\mathrm{90}° \\ $$$$\mathrm{if}\:\angle\mathrm{AHB}=\angle\mathrm{BHD}=\angle\mathrm{DHF} \\ $$$$\mathrm{then}\:\angle\mathrm{AHB}=\angle\mathrm{BHD}=\angle\mathrm{DHF}=\frac{\pi}{\mathrm{6}}=\mathrm{30}° \\ $$$$ \\ $$$$\mathrm{BG}={r}−\frac{\mathrm{2}{r}}{\mathrm{3}}=\frac{{r}}{\mathrm{3}}=\mathrm{GD} \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{say}\:\angle\mathrm{BHG}={x}\Rightarrow\angle\mathrm{GHD}=\frac{\pi}{\mathrm{6}}−{x} \\ $$$$\bigtriangleup\mathrm{HBG},\angle\mathrm{HGB}=\pi−\alpha \\ $$$$\angle\mathrm{HBG}=\pi−{x}−\left(\pi−\alpha\right)=\alpha−{x} \\ $$$$\frac{\mathrm{HG}}{\mathrm{sin}\:\left(\alpha−{x}\right)}=\frac{\mathrm{BG}}{\mathrm{sin}\:{x}} \\ $$$$\bigtriangleup\mathrm{GHD} \\ $$$$\angle\mathrm{HGD}=\alpha \\ $$$$\angle\mathrm{GHD}=\frac{\pi}{\mathrm{6}}−{x} \\ $$$$\angle\mathrm{HDG}=\pi−\alpha−\left(\frac{\pi}{\mathrm{6}}−{x}\right)=\frac{\mathrm{5}\pi}{\mathrm{6}}+{x}−\alpha \\ $$$$\frac{\mathrm{HG}}{\mathrm{sin}\:\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+{x}−\alpha\right)}=\frac{\mathrm{GD}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−{x}\right)}=\frac{\mathrm{BG}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−{x}\right)} \\ $$$$\frac{\mathrm{sin}\:{x}}{\mid\mathrm{sin}\:\left(\alpha−{x}\right)\mid}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−{x}\right)}{\mid\mathrm{sin}\:\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+{x}−\alpha\right)\mid} \\ $$$$\bigtriangleup\mathrm{HAD} \\ $$$$\angle\mathrm{HAD}=\pi−\frac{\pi}{\mathrm{3}}−\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+{x}−\alpha\right)=\alpha−{x}−\frac{\pi}{\mathrm{6}} \\ $$$$\bigtriangleup\mathrm{HAB} \\ $$$$\frac{\mathrm{HB}}{\mathrm{sin}\:\left(\alpha−{x}−\frac{\pi}{\mathrm{6}}\right)}=\frac{\mathrm{AB}}{\mathrm{sin}\:\frac{\pi}{\mathrm{6}}} \\ $$$$\bigtriangleup\mathrm{HBD} \\ $$$$\frac{\mathrm{BD}}{\mathrm{sin}\:\frac{\pi}{\mathrm{6}}}=\frac{\mathrm{HB}}{\mathrm{sin}\:\left(\frac{\mathrm{5}\pi}{\mathrm{6}}+{x}−\alpha\right)} \\ $$$$\mathrm{AB}=\mathrm{BD}\Rightarrow\alpha−{x}−\frac{\pi}{\mathrm{6}}=\frac{\mathrm{5}\pi}{\mathrm{6}}+{x}−\alpha \\ $$$$\mathrm{2}\alpha−\mathrm{2}{x}=\pi\Rightarrow\alpha=\frac{\pi}{\mathrm{2}}+{x} \\ $$$$\frac{\mathrm{sin}\:{x}}{\mid\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+{x}−{x}\right)\mid}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−{x}\right)}{\mid\mathrm{sin}\:\left(\frac{\mathrm{5}\pi}{\mathrm{6}}−\frac{\pi}{\mathrm{2}}\right)\mid} \\ $$$$\mathrm{sin}\:{x}\centerdot\mid\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}\right)\mid=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−{x}\right) \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:{x}=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−{x}\right) \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:{x} \\ $$$$\mathrm{tan}\:{x}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${x}=\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\alpha=\frac{\pi}{\mathrm{2}}+\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\mathrm{Please}\:\mathrm{check}. \\ $$

Commented by Rasheed Soomro last updated on 27/Sep/16

GREAT approach !!! I didn′t understand some lines: △GHD ⋮ ∠HDG=π−α−((π/6)−x)=((5π)/6)+x−α ((HG)/(sin (((5π)/6)+^(?) α−^(?) x)))=((GD)/(sin ((π/6)−x)))=((BG)/(sin ((π/6)−x))) ..... ...

$$\mathcal{GREAT}\:\:{approach}\:!!! \\ $$$${I}\:{didn}'{t}\:{understand}\:{some}\:{lines}: \\ $$$$\bigtriangleup\mathrm{GHD} \\ $$$$\vdots \\ $$$$\angle\mathrm{HDG}=\pi−\alpha−\left(\frac{\pi}{\mathrm{6}}−{x}\right)=\frac{\mathrm{5}\pi}{\mathrm{6}}+{x}−\alpha \\ $$$$\frac{\mathrm{HG}}{\mathrm{sin}\:\left(\frac{\mathrm{5}\pi}{\mathrm{6}}\overset{?} {+}\alpha\overset{?} {−}{x}\right)}=\frac{\mathrm{GD}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−{x}\right)}=\frac{\mathrm{BG}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−{x}\right)}\:\: \\ $$$$..... \\ $$$$... \\ $$

Commented by prakash jain last updated on 27/Sep/16

Yes. My mistake. I will correct.

$$\mathrm{Yes}.\:\mathrm{My}\:\mathrm{mistake}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{correct}. \\ $$

Answered by prakash jain last updated on 02/Oct/16

In comments.

$$\mathrm{In}\:\mathrm{comments}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com