
Question and Answers Forum
Question Number 79499 by jagoll last updated on 25/Jan/20
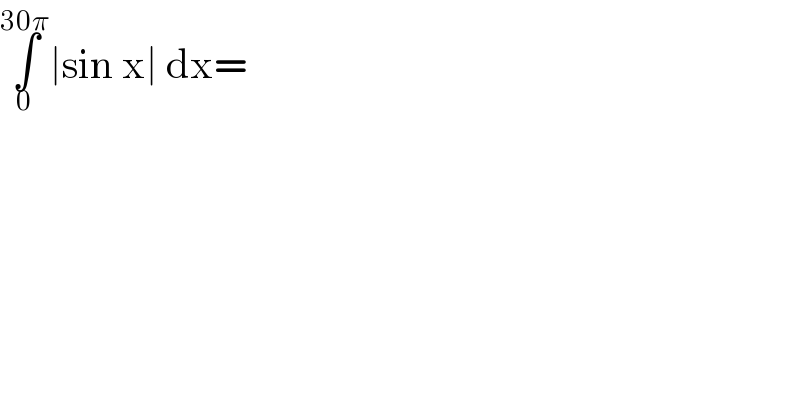
Commented by john santu last updated on 25/Jan/20
![y = ∣sin x∣ is even function and periodic with periode = π ∫_0 ^(30π) ∣sin x∣dx = ∫_0 ^π ∣sin x∣dx+∫_π ^(2π) ∣sin x∣dx+ ...+∫_(29π) ^(30) ∣sin x∣dx = 30×[2∫_0 ^(π/2) sin xdx] = 60×1 = 60.](Q79501.png)
Commented by mathmax by abdo last updated on 25/Jan/20
![∫_0 ^(30π) ∣sinx∣dx =Σ_(k=0) ^(29) ∫_(kπ) ^((k+1)π) ∣sinx∣dx =_(x=kπ +t) =Σ_(k=0) ^(29) ∫_0 ^π ∣sin(kπ +t)dt =Σ_(k=0) ^(29) ∫_0 ^π ∣sint∣dt =Σ_(k=0) ^(29) ∫_0 ^π sint dt =Σ_(k=0) ^(29) [−cost]_0 ^π =2Σ_(k=0) ^(29) (1) =2×30 =60](Q79523.png)
| ||
Question and Answers Forum | ||
Question Number 79499 by jagoll last updated on 25/Jan/20 | ||
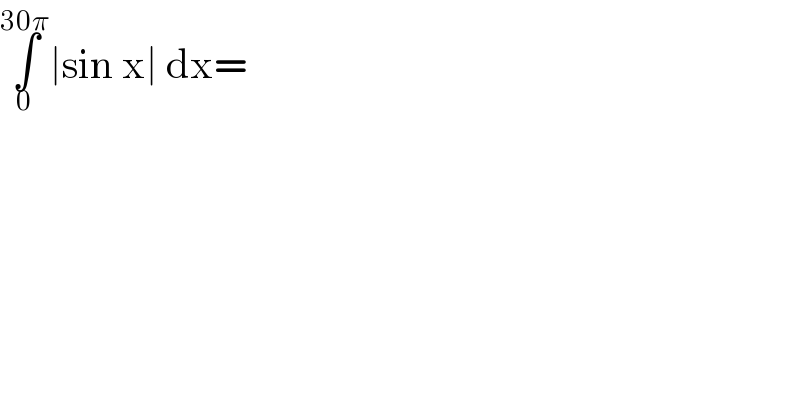 | ||
Commented by john santu last updated on 25/Jan/20 | ||
![y = ∣sin x∣ is even function and periodic with periode = π ∫_0 ^(30π) ∣sin x∣dx = ∫_0 ^π ∣sin x∣dx+∫_π ^(2π) ∣sin x∣dx+ ...+∫_(29π) ^(30) ∣sin x∣dx = 30×[2∫_0 ^(π/2) sin xdx] = 60×1 = 60.](Q79501.png) | ||
Commented by mathmax by abdo last updated on 25/Jan/20 | ||
![∫_0 ^(30π) ∣sinx∣dx =Σ_(k=0) ^(29) ∫_(kπ) ^((k+1)π) ∣sinx∣dx =_(x=kπ +t) =Σ_(k=0) ^(29) ∫_0 ^π ∣sin(kπ +t)dt =Σ_(k=0) ^(29) ∫_0 ^π ∣sint∣dt =Σ_(k=0) ^(29) ∫_0 ^π sint dt =Σ_(k=0) ^(29) [−cost]_0 ^π =2Σ_(k=0) ^(29) (1) =2×30 =60](Q79523.png) | ||