
Question and Answers Forum
Question Number 79516 by Pratah last updated on 25/Jan/20
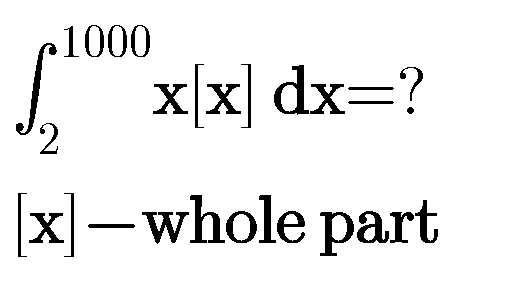
Commented by abdomathmax last updated on 25/Jan/20
![I =Σ_(k=2) ^(999) ∫_k ^(k+1) kx dx =Σ_(k=2) ^(999) k [(x^2 /2)]_k ^(k+1) =Σ_(k=2) ^(999) (k/2){ (k+1)^2 −k^2 } =Σ_(k=2) ^(999) (k/2){ k^2 +2k+1−k^2 } =(1/2)Σ_(k=2) ^(999) k{2k+1} =(1/2)Σ_(k=2) ^(999) (2k^2 +k) =Σ_(k=2) ^(999) k^2 +(1/2)Σ_(k=2) ^(999) k =Σ_(k=1) ^(999) k^2 −1 +(1/2)Σ_(k=1) ^(999) k−(1/2) we know Σ_(k=1) ^n k^2 =((n(n+1)(2n+1))/6) ⇒ I =((999(1000)(2×999 +1))/6) +(1/2)×((999(1000))/2) −(3/2) rest finishing the calculus...](Q79517.png)
Commented by Pratah last updated on 25/Jan/20

Commented by mathmax by abdo last updated on 25/Jan/20
| ||
Question and Answers Forum | ||
Question Number 79516 by Pratah last updated on 25/Jan/20 | ||
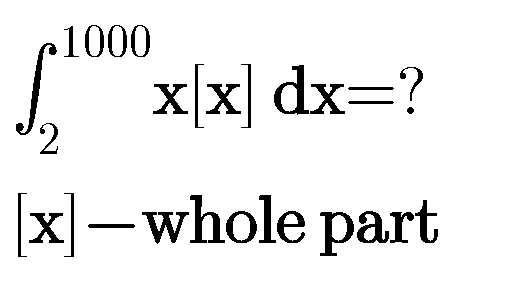 | ||
Commented by abdomathmax last updated on 25/Jan/20 | ||
![I =Σ_(k=2) ^(999) ∫_k ^(k+1) kx dx =Σ_(k=2) ^(999) k [(x^2 /2)]_k ^(k+1) =Σ_(k=2) ^(999) (k/2){ (k+1)^2 −k^2 } =Σ_(k=2) ^(999) (k/2){ k^2 +2k+1−k^2 } =(1/2)Σ_(k=2) ^(999) k{2k+1} =(1/2)Σ_(k=2) ^(999) (2k^2 +k) =Σ_(k=2) ^(999) k^2 +(1/2)Σ_(k=2) ^(999) k =Σ_(k=1) ^(999) k^2 −1 +(1/2)Σ_(k=1) ^(999) k−(1/2) we know Σ_(k=1) ^n k^2 =((n(n+1)(2n+1))/6) ⇒ I =((999(1000)(2×999 +1))/6) +(1/2)×((999(1000))/2) −(3/2) rest finishing the calculus...](Q79517.png) | ||
Commented by Pratah last updated on 25/Jan/20 | ||
 | ||
Commented by mathmax by abdo last updated on 25/Jan/20 | ||
 | ||