Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 79634 by TawaTawa last updated on 26/Jan/20

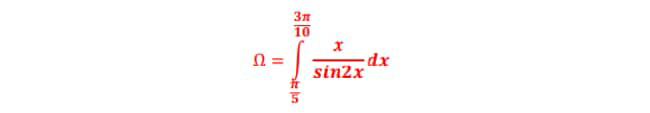
Commented by mathmax by abdo last updated on 27/Jan/20
$Ω =∫_(π/5) ^((3π)/(10)) (x/(sin(2x)))dx changement x=(π/2)−t givet=(π/2)−x Ω=∫_((3π)/(10)) ^(π/5) (((π/2)−t)/(sin(2t)))(−dt) =(π/2)∫_(π/5) ^((3π)/(10)) (dt/(sin(2t))) −Ω ⇒ 2Ω =(π/2) ∫_(π/5) ^((3π)/(10)) (dt/(sin(2t))) changement tant =u give ∫_(π/5) ^((3π)/(10)) (dt/(sin(2t))) =∫_(tan((π/5))) ^(tan(((3π)/(10)))) (1/((2u)/(1+u^2 )))×(du/(1+u^2 )) =(1/2)[ln∣u∣]_(tan((π/5))) ^(tan(((3π)/(10)))) =(1/2){ln(tan(((3π)/(10)))−ln(tan((π/5)))} =(1/2){ ln(tan((π/2)−(π/5)))−ln(tan((π/5)))} =(1/2){ln((1/(tan((π/5)))))−ln(tan((π/5)))}=−ln(tan((π/5))) ⇒ Ω=−(π/4)ln(tan((π/5)))$
$Ω = \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{x}{s i n (2 x)} d x c h a n g e m e n t x = \frac{π}{2} - t g i v e t = \frac{π}{2} - x$ $Ω = \int_{\frac{3 π}{10}}^{\frac{π}{5}} \frac{\frac{π}{2} - t}{s i n (2 t)} (- d t) = \frac{π}{2} \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{d t}{s i n (2 t)} - Ω \Rightarrow$ $2 Ω = \frac{π}{2} \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{d t}{s i n (2 t)} c h a n g e m e n t t a n t = u g i v e$ $\int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{d t}{s i n (2 t)} = \int_{t a n (\frac{π}{5})}^{t a n (\frac{3 π}{10})} \frac{1}{\frac{2 u}{1 + u^{2}}} \times \frac{d u}{1 + u^{2}} = \frac{1}{2} {[l n ∣ u ∣]}_{t a n (\frac{π}{5})}^{t a n (\frac{3 π}{10})}$ $= \frac{1}{2} {l n (t a n (\frac{3 π}{10}) - l n (t a n (\frac{π}{5}))}$ $= \frac{1}{2} {l n (t a n (\frac{π}{2} - \frac{π}{5})) - l n (t a n (\frac{π}{5}))}$ $= \frac{1}{2} {l n (\frac{1}{t a n (\frac{π}{5})}) - l n (t a n (\frac{π}{5}))} = - l n (t a n (\frac{π}{5})) \Rightarrow$ $Ω = - \frac{π}{4} l n (t a n (\frac{π}{5}))$
Commented by TawaTawa last updated on 27/Jan/20

$God bless you sir$
Commented by mathmax by abdo last updated on 29/Jan/20

$y o u a r e w e l c o m e$
	Answered by mind is power last updated on 27/Jan/20

	$Ω = \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{x}{s i n (2 x)} d x$ $\int_{a}^{b} f (x) d x = \int_{a}^{b} f (a + b - x) d x \Rightarrow$ $\int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{\frac{π}{2} - x}{s i n (2 (\frac{π}{2} - x))} d x = \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{\frac{π}{2} - x}{s i n (π - 2 x)} d x = - \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{x}{s i n (2 x)} +$ $\frac{π}{2} \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{d x}{s i n (2 x)} \Rightarrow$ $\Rightarrow 2 \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{x d x}{s i n (2 x)} = \frac{π}{2} \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{d x}{s i n (2 x)} = \frac{π}{4} \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{d x}{s i n (x) c o s (x)}$ $= \frac{π}{4} \int_{\frac{π}{5}}^{\frac{3 π}{10}} \frac{c o s (x)}{s i n (x) . {c o s}^{2} (x)} d x = \frac{π}{4} \int_{\frac{π}{5}}^{\frac{3 π}{10}} c o t (x) . (1 + {t g}^{2} (x)) d x$ $= \frac{π}{4} \int_{\frac{π}{5}}^{\frac{3 π}{10}} t g (\frac{π}{2} - x) d (t g (x))$ $= \frac{π}{8} {[- {t g}^{2} (\frac{π}{2} - x)]}_{\frac{π}{5}}^{\frac{3 π}{10}} = - \frac{π}{8} ({t g}^{2} (\frac{π}{5}) - {t g}^{2} (\frac{3 π}{10}))$ $w e c a n f i n d e x a c t t g (\frac{π}{5}), a n d t g (\frac{3 π}{10})$
	Commented by TawaTawa last updated on 27/Jan/20

	$God bless you sir$
	Commented by mind is power last updated on 27/Jan/20

	$t h a k y o u, w i t h e p l e a s u r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum