Question and Answers Forum
Question Number 79649 by john santu last updated on 27/Jan/20

Commented byjohn santu last updated on 27/Jan/20
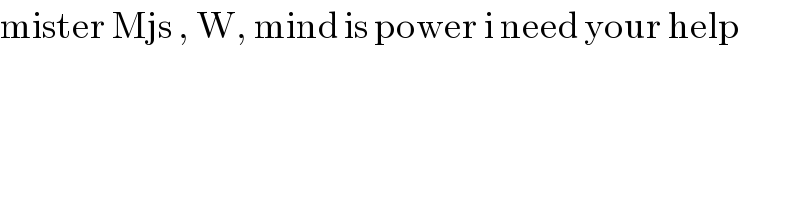
Commented bymind is power last updated on 27/Jan/20
![a,x_1 ,x_2 ,ar Ap s=2a(1+r) x_1 +x_2 =2a(1+r)−a(1+r)=a(1+r) x_3 +x_4 +x_5 +x_6 =2(ar+ar^2 ) x_7 +........+x_(12) =3(ar^2 +ar^4 ) we get Σx_k =Σ(a+2ar+3ar^2 +.......)+Σ(ar+2ar^2 +........) =aΣ(1+2r+3r^2 +....)+arΣ(1+2r+3r^2 +.......) =(a+ar)Σ(1+2r+3r^2 +....) Σ_(k≥1) kr^(k−1) =Σ(d/dr)(r^k )=(d/dr)Σr^k =(d/dr)((r/(1−r)))=(1/((1−r)^2 )) ⇒((a(1+r))/((1−r)^2 ))=((21a)/(16(1−r))),r∈]0,1[ ⇒21(1−r)=16(1+r)⇒5=37r⇒r=(5/(37))](Q79657.png)
Commented byjohn santu last updated on 27/Jan/20
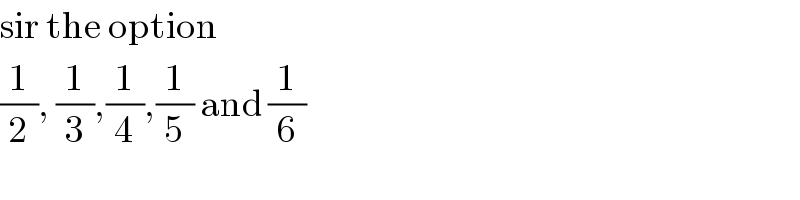
Commented byjohn santu last updated on 27/Jan/20

Commented byjohn santu last updated on 27/Jan/20
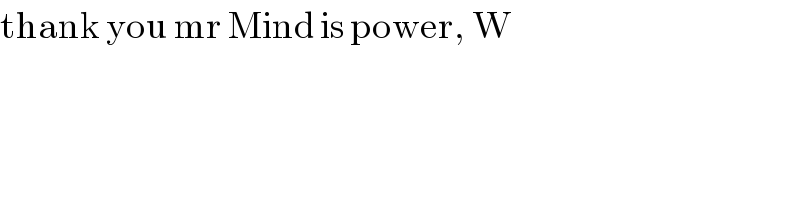
Commented bymind is power last updated on 27/Jan/20

Answered by mr W last updated on 27/Jan/20