Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 79697 by ajfour last updated on 27/Jan/20

Commented by ajfour last updated on 27/Jan/20

Find coordinates of A,B,C if each coloured regions I→IV have the same area.

$${Find}\:{coordinates}\:{of}\:{A},{B},{C}\:{if} \\ $$$${each}\:{coloured}\:{regions}\:{I}\rightarrow{IV} \\ $$$${have}\:{the}\:{same}\:{area}. \\ $$

Answered by ajfour last updated on 27/Jan/20

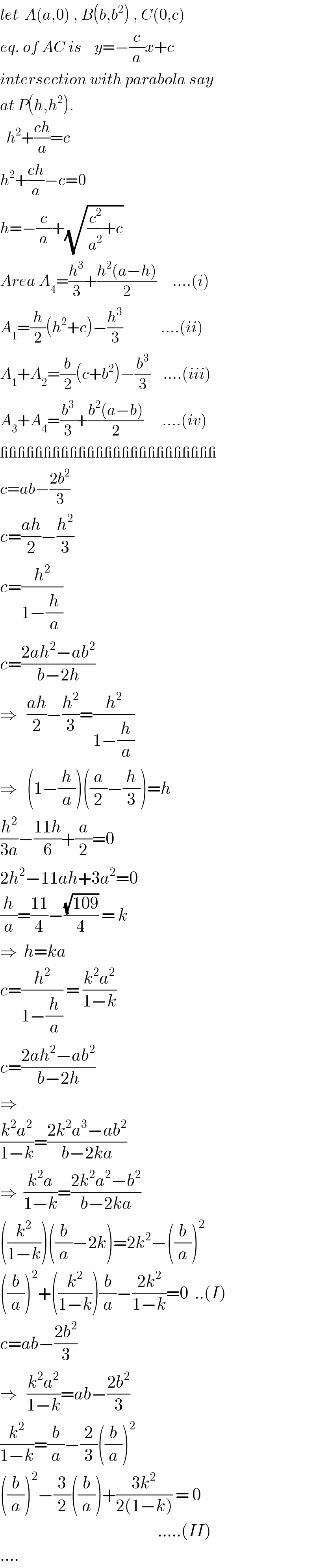
let A(a,0) , B(b,b^2 ) , C(0,c) eq. of AC is y=−(c/a)x+c intersection with parabola say at P(h,h^2 ). h^2 +((ch)/a)=c h^2 +((ch)/a)−c=0 h=−(c/a)+(√((c^2 /a^2 )+c)) Area A_4 =(h^3 /3)+((h^2 (a−h))/2) ....(i) A_1 =(h/2)(h^2 +c)−(h^3 /3) ....(ii) A_1 +A_2 =(b/2)(c+b^2 )−(b^3 /3) ....(iii) A_3 +A_4 =(b^3 /3)+((b^2 (a−b))/2) ....(iv) _________________________ c=ab−((2b^2 )/3) c=((ah)/2)−(h^2 /3) c=(h^2 /(1−(h/a))) c=((2ah^2 −ab^2 )/(b−2h)) ⇒ ((ah)/2)−(h^2 /3)=(h^2 /(1−(h/a))) ⇒ (1−(h/a))((a/2)−(h/3))=h (h^2 /(3a))−((11h)/6)+(a/2)=0 2h^2 −11ah+3a^2 =0 (h/a)=((11)/4)−((√(109))/4) = k ⇒ h=ka c=(h^2 /(1−(h/a))) = ((k^2 a^2 )/(1−k)) c=((2ah^2 −ab^2 )/(b−2h)) ⇒ ((k^2 a^2 )/(1−k))=((2k^2 a^3 −ab^2 )/(b−2ka)) ⇒ ((k^2 a)/(1−k))=((2k^2 a^2 −b^2 )/(b−2ka)) ((k^2 /(1−k)))((b/a)−2k)=2k^2 −((b/a))^2 ((b/a))^2 +((k^2 /(1−k)))(b/a)−((2k^2 )/(1−k))=0 ..(I) c=ab−((2b^2 )/3) ⇒ ((k^2 a^2 )/(1−k))=ab−((2b^2 )/3) (k^2 /(1−k))=(b/a)−(2/3)((b/a))^2 ((b/a))^2 −(3/2)((b/a))+((3k^2 )/(2(1−k))) = 0 .....(II) ....

$${let}\:\:{A}\left({a},\mathrm{0}\right)\:,\:{B}\left({b},{b}^{\mathrm{2}} \right)\:,\:{C}\left(\mathrm{0},{c}\right) \\ $$$${eq}.\:{of}\:{AC}\:{is}\:\:\:\:{y}=−\frac{{c}}{{a}}{x}+{c} \\ $$$${intersection}\:{with}\:{parabola}\:{say} \\ $$$${at}\:{P}\left({h},{h}^{\mathrm{2}} \right). \\ $$$$\:\:{h}^{\mathrm{2}} +\frac{{ch}}{{a}}={c} \\ $$$${h}^{\mathrm{2}} +\frac{{ch}}{{a}}−{c}=\mathrm{0} \\ $$$${h}=−\frac{{c}}{{a}}+\sqrt{\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+{c}} \\ $$$${Area}\:{A}_{\mathrm{4}} =\frac{{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{h}^{\mathrm{2}} \left({a}−{h}\right)}{\mathrm{2}}\:\:\:\:\:....\left({i}\right) \\ $$$${A}_{\mathrm{1}} =\frac{{h}}{\mathrm{2}}\left({h}^{\mathrm{2}} +{c}\right)−\frac{{h}^{\mathrm{3}} }{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:....\left({ii}\right) \\ $$$${A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\frac{{b}}{\mathrm{2}}\left({c}+{b}^{\mathrm{2}} \right)−\frac{{b}^{\mathrm{3}} }{\mathrm{3}}\:\:\:\:....\left({iii}\right) \\ $$$${A}_{\mathrm{3}} +{A}_{\mathrm{4}} =\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} \left({a}−{b}\right)}{\mathrm{2}}\:\:\:\:\:\:....\left({iv}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${c}={ab}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${c}=\frac{{ah}}{\mathrm{2}}−\frac{{h}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${c}=\frac{{h}^{\mathrm{2}} }{\mathrm{1}−\frac{{h}}{{a}}} \\ $$$${c}=\frac{\mathrm{2}{ah}^{\mathrm{2}} −{ab}^{\mathrm{2}} }{{b}−\mathrm{2}{h}} \\ $$$$\Rightarrow\:\:\:\frac{{ah}}{\mathrm{2}}−\frac{{h}^{\mathrm{2}} }{\mathrm{3}}=\frac{{h}^{\mathrm{2}} }{\mathrm{1}−\frac{{h}}{{a}}} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{1}−\frac{{h}}{{a}}\right)\left(\frac{{a}}{\mathrm{2}}−\frac{{h}}{\mathrm{3}}\right)={h} \\ $$$$\frac{{h}^{\mathrm{2}} }{\mathrm{3}{a}}−\frac{\mathrm{11}{h}}{\mathrm{6}}+\frac{{a}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{2}{h}^{\mathrm{2}} −\mathrm{11}{ah}+\mathrm{3}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{h}}{{a}}=\frac{\mathrm{11}}{\mathrm{4}}−\frac{\sqrt{\mathrm{109}}}{\mathrm{4}}\:=\:{k} \\ $$$$\Rightarrow\:\:{h}={ka} \\ $$$${c}=\frac{{h}^{\mathrm{2}} }{\mathrm{1}−\frac{{h}}{{a}}}\:=\:\frac{{k}^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{1}−{k}} \\ $$$${c}=\frac{\mathrm{2}{ah}^{\mathrm{2}} −{ab}^{\mathrm{2}} }{{b}−\mathrm{2}{h}} \\ $$$$\Rightarrow\:\: \\ $$$$\frac{{k}^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{1}−{k}}=\frac{\mathrm{2}{k}^{\mathrm{2}} {a}^{\mathrm{3}} −{ab}^{\mathrm{2}} }{{b}−\mathrm{2}{ka}} \\ $$$$\Rightarrow\:\:\frac{{k}^{\mathrm{2}} {a}}{\mathrm{1}−{k}}=\frac{\mathrm{2}{k}^{\mathrm{2}} {a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}−\mathrm{2}{ka}} \\ $$$$\left(\frac{{k}^{\mathrm{2}} }{\mathrm{1}−{k}}\right)\left(\frac{{b}}{{a}}−\mathrm{2}{k}\right)=\mathrm{2}{k}^{\mathrm{2}} −\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} \\ $$$$\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} +\left(\frac{{k}^{\mathrm{2}} }{\mathrm{1}−{k}}\right)\frac{{b}}{{a}}−\frac{\mathrm{2}{k}^{\mathrm{2}} }{\mathrm{1}−{k}}=\mathrm{0}\:\:..\left({I}\right) \\ $$$${c}={ab}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\frac{{k}^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{1}−{k}}={ab}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\frac{{k}^{\mathrm{2}} }{\mathrm{1}−{k}}=\frac{{b}}{{a}}−\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} \:\:\: \\ $$$$\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{{b}}{{a}}\right)+\frac{\mathrm{3}{k}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−{k}\right)}\:=\:\mathrm{0}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....\left({II}\right) \\ $$$$.... \\ $$

Commented by ajfour last updated on 27/Jan/20

I just have to check, seems sure, that they′ll conflict..

$${I}\:{just}\:{have}\:{to}\:{check},\:{seems} \\ $$$${sure},\:{that}\:{they}'{ll}\:{conflict}.. \\ $$

Answered by mr W last updated on 28/Jan/20

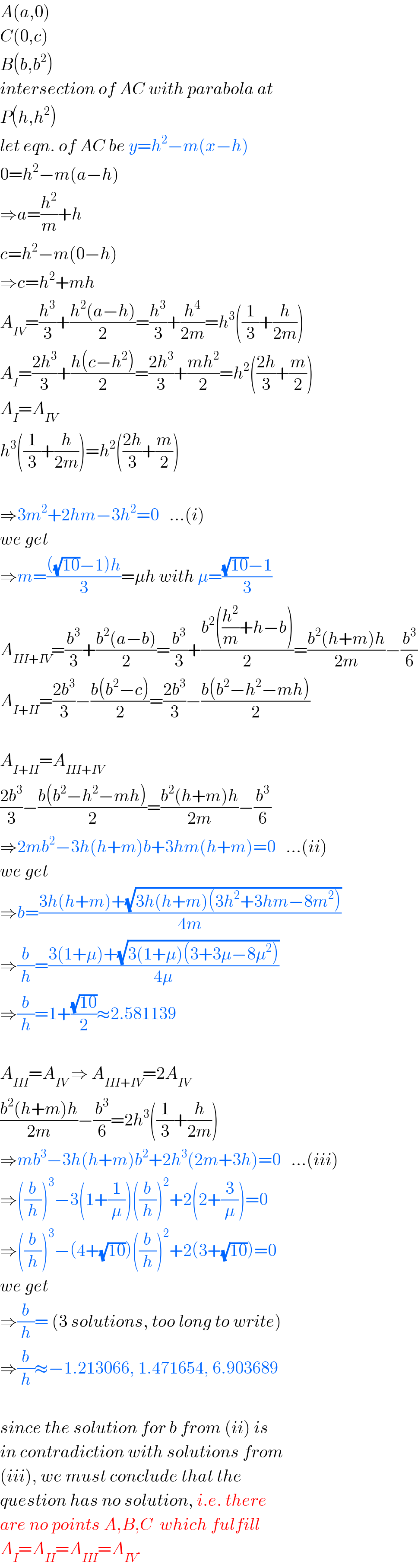
A(a,0) C(0,c) B(b,b^2 ) intersection of AC with parabola at P(h,h^2 ) let eqn. of AC be y=h^2 −m(x−h) 0=h^2 −m(a−h) ⇒a=(h^2 /m)+h c=h^2 −m(0−h) ⇒c=h^2 +mh A_(IV) =(h^3 /3)+((h^2 (a−h))/2)=(h^3 /3)+(h^4 /(2m))=h^3 ((1/3)+(h/(2m))) A_I =((2h^3 )/3)+((h(c−h^2 ))/2)=((2h^3 )/3)+((mh^2 )/2)=h^2 (((2h)/3)+(m/2)) A_I =A_(IV) h^3 ((1/3)+(h/(2m)))=h^2 (((2h)/3)+(m/2)) ⇒3m^2 +2hm−3h^2 =0 ...(i) we get ⇒m=((((√(10))−1)h)/3)=μh with μ=(((√(10))−1)/3) A_(III+IV) =(b^3 /3)+((b^2 (a−b))/2)=(b^3 /3)+((b^2 ((h^2 /m)+h−b))/2)=((b^2 (h+m)h)/(2m))−(b^3 /6) A_(I+II) =((2b^3 )/3)−((b(b^2 −c))/2)=((2b^3 )/3)−((b(b^2 −h^2 −mh))/2) A_(I+II) =A_(III+IV) ((2b^3 )/3)−((b(b^2 −h^2 −mh))/2)=((b^2 (h+m)h)/(2m))−(b^3 /6) ⇒2mb^2 −3h(h+m)b+3hm(h+m)=0 ...(ii) we get ⇒b=((3h(h+m)+(√(3h(h+m)(3h^2 +3hm−8m^2 ))))/(4m)) ⇒(b/h)=((3(1+μ)+(√(3(1+μ)(3+3μ−8μ^2 ))))/(4μ)) ⇒(b/h)=1+((√(10))/2)≈2.581139 A_(III) =A_(IV) ⇒ A_(III+IV) =2A_(IV) ((b^2 (h+m)h)/(2m))−(b^3 /6)=2h^3 ((1/3)+(h/(2m))) ⇒mb^3 −3h(h+m)b^2 +2h^3 (2m+3h)=0 ...(iii) ⇒((b/h))^3 −3(1+(1/μ))((b/h))^2 +2(2+(3/μ))=0 ⇒((b/h))^3 −(4+(√(10)))((b/h))^2 +2(3+(√(10)))=0 we get ⇒(b/h)= (3 solutions, too long to write) ⇒(b/h)≈−1.213066, 1.471654, 6.903689 since the solution for b from (ii) is in contradiction with solutions from (iii), we must conclude that the question has no solution, i.e. there are no points A,B,C which fulfill A_I =A_(II) =A_(III) =A_(IV) .

$${A}\left({a},\mathrm{0}\right) \\ $$$${C}\left(\mathrm{0},{c}\right) \\ $$$${B}\left({b},{b}^{\mathrm{2}} \right) \\ $$$${intersection}\:{of}\:{AC}\:{with}\:{parabola}\:{at} \\ $$$${P}\left({h},{h}^{\mathrm{2}} \right) \\ $$$${let}\:{eqn}.\:{of}\:{AC}\:{be}\:{y}={h}^{\mathrm{2}} −{m}\left({x}−{h}\right) \\ $$$$\mathrm{0}={h}^{\mathrm{2}} −{m}\left({a}−{h}\right) \\ $$$$\Rightarrow{a}=\frac{{h}^{\mathrm{2}} }{{m}}+{h} \\ $$$${c}={h}^{\mathrm{2}} −{m}\left(\mathrm{0}−{h}\right) \\ $$$$\Rightarrow{c}={h}^{\mathrm{2}} +{mh} \\ $$$${A}_{{IV}} =\frac{{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{h}^{\mathrm{2}} \left({a}−{h}\right)}{\mathrm{2}}=\frac{{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{h}^{\mathrm{4}} }{\mathrm{2}{m}}={h}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{{h}}{\mathrm{2}{m}}\right) \\ $$$${A}_{{I}} =\frac{\mathrm{2}{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{h}\left({c}−{h}^{\mathrm{2}} \right)}{\mathrm{2}}=\frac{\mathrm{2}{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{mh}^{\mathrm{2}} }{\mathrm{2}}={h}^{\mathrm{2}} \left(\frac{\mathrm{2}{h}}{\mathrm{3}}+\frac{{m}}{\mathrm{2}}\right) \\ $$$${A}_{{I}} ={A}_{{IV}} \\ $$$${h}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{{h}}{\mathrm{2}{m}}\right)={h}^{\mathrm{2}} \left(\frac{\mathrm{2}{h}}{\mathrm{3}}+\frac{{m}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\Rightarrow\mathrm{3}{m}^{\mathrm{2}} +\mathrm{2}{hm}−\mathrm{3}{h}^{\mathrm{2}} =\mathrm{0}\:\:\:...\left({i}\right) \\ $$$${we}\:{get} \\ $$$$\Rightarrow{m}=\frac{\left(\sqrt{\mathrm{10}}−\mathrm{1}\right){h}}{\mathrm{3}}=\mu{h}\:{with}\:\mu=\frac{\sqrt{\mathrm{10}}−\mathrm{1}}{\mathrm{3}} \\ $$$${A}_{{III}+{IV}} =\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} \left({a}−{b}\right)}{\mathrm{2}}=\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} \left(\frac{{h}^{\mathrm{2}} }{{m}}+{h}−{b}\right)}{\mathrm{2}}=\frac{{b}^{\mathrm{2}} \left({h}+{m}\right){h}}{\mathrm{2}{m}}−\frac{{b}^{\mathrm{3}} }{\mathrm{6}} \\ $$$${A}_{{I}+{II}} =\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{3}}−\frac{{b}\left({b}^{\mathrm{2}} −{c}\right)}{\mathrm{2}}=\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{3}}−\frac{{b}\left({b}^{\mathrm{2}} −{h}^{\mathrm{2}} −{mh}\right)}{\mathrm{2}} \\ $$$$ \\ $$$${A}_{{I}+{II}} ={A}_{{III}+{IV}} \\ $$$$\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{3}}−\frac{{b}\left({b}^{\mathrm{2}} −{h}^{\mathrm{2}} −{mh}\right)}{\mathrm{2}}=\frac{{b}^{\mathrm{2}} \left({h}+{m}\right){h}}{\mathrm{2}{m}}−\frac{{b}^{\mathrm{3}} }{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{2}{mb}^{\mathrm{2}} −\mathrm{3}{h}\left({h}+{m}\right){b}+\mathrm{3}{hm}\left({h}+{m}\right)=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$${we}\:{get} \\ $$$$\Rightarrow{b}=\frac{\mathrm{3}{h}\left({h}+{m}\right)+\sqrt{\mathrm{3}{h}\left({h}+{m}\right)\left(\mathrm{3}{h}^{\mathrm{2}} +\mathrm{3}{hm}−\mathrm{8}{m}^{\mathrm{2}} \right)}}{\mathrm{4}{m}} \\ $$$$\Rightarrow\frac{{b}}{{h}}=\frac{\mathrm{3}\left(\mathrm{1}+\mu\right)+\sqrt{\mathrm{3}\left(\mathrm{1}+\mu\right)\left(\mathrm{3}+\mathrm{3}\mu−\mathrm{8}\mu^{\mathrm{2}} \right)}}{\mathrm{4}\mu} \\ $$$$\Rightarrow\frac{{b}}{{h}}=\mathrm{1}+\frac{\sqrt{\mathrm{10}}}{\mathrm{2}}\approx\mathrm{2}.\mathrm{581139} \\ $$$$ \\ $$$${A}_{{III}} ={A}_{{IV}} \:\Rightarrow\:{A}_{{III}+{IV}} =\mathrm{2}{A}_{{IV}} \\ $$$$\frac{{b}^{\mathrm{2}} \left({h}+{m}\right){h}}{\mathrm{2}{m}}−\frac{{b}^{\mathrm{3}} }{\mathrm{6}}=\mathrm{2}{h}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{{h}}{\mathrm{2}{m}}\right) \\ $$$$\Rightarrow{mb}^{\mathrm{3}} −\mathrm{3}{h}\left({h}+{m}\right){b}^{\mathrm{2}} +\mathrm{2}{h}^{\mathrm{3}} \left(\mathrm{2}{m}+\mathrm{3}{h}\right)=\mathrm{0}\:\:\:...\left({iii}\right) \\ $$$$\Rightarrow\left(\frac{{b}}{{h}}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{1}+\frac{\mathrm{1}}{\mu}\right)\left(\frac{{b}}{{h}}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{2}+\frac{\mathrm{3}}{\mu}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{{b}}{{h}}\right)^{\mathrm{3}} −\left(\mathrm{4}+\sqrt{\mathrm{10}}\right)\left(\frac{{b}}{{h}}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{10}}\right)=\mathrm{0} \\ $$$${we}\:{get} \\ $$$$\Rightarrow\frac{{b}}{{h}}=\:\left(\mathrm{3}\:{solutions},\:{too}\:{long}\:{to}\:{write}\right) \\ $$$$\Rightarrow\frac{{b}}{{h}}\approx−\mathrm{1}.\mathrm{213066},\:\mathrm{1}.\mathrm{471654},\:\mathrm{6}.\mathrm{903689} \\ $$$$ \\ $$$${since}\:{the}\:{solution}\:{for}\:{b}\:{from}\:\left({ii}\right)\:{is} \\ $$$${in}\:{contradiction}\:{with}\:{solutions}\:{from} \\ $$$$\left({iii}\right),\:{we}\:{must}\:{conclude}\:{that}\:{the} \\ $$$${question}\:{has}\:{no}\:{solution},\:{i}.{e}.\:{there} \\ $$$${are}\:{no}\:{points}\:{A},{B},{C}\:\:{which}\:{fulfill}\: \\ $$$${A}_{{I}} ={A}_{{II}} ={A}_{{III}} ={A}_{{IV}} . \\ $$

Commented by john santu last updated on 27/Jan/20

AC : cx + ay = ac

$$\mathrm{AC}\::\:\mathrm{cx}\:+\:\mathrm{ay}\:=\:\mathrm{ac}\: \\ $$

Commented by mr W last updated on 28/Jan/20

for AC i use the equation in form of y=h^2 −m(x−h). it goes through point P(h,h^2 ) [the same as D(d,d^2 ) in your workings] and has the inclination −m. such that A_I =A_(IV) we have m=((((√(10))−1)h)/3).

$${for}\:{AC}\:{i}\:{use}\:{the}\:{equation}\:{in}\:{form}\:{of} \\ $$$${y}={h}^{\mathrm{2}} −{m}\left({x}−{h}\right). \\ $$$${it}\:{goes}\:{through}\:{point}\:{P}\left({h},{h}^{\mathrm{2}} \right)\:\left[{the}\:{same}\right. \\ $$$$\left.{as}\:{D}\left({d},{d}^{\mathrm{2}} \right)\:{in}\:{your}\:{workings}\right]\:{and}\:{has} \\ $$$${the}\:{inclination}\:−{m}. \\ $$$${such}\:{that}\:{A}_{{I}} ={A}_{{IV}} \:{we}\:{have} \\ $$$${m}=\frac{\left(\sqrt{\mathrm{10}}−\mathrm{1}\right){h}}{\mathrm{3}}. \\ $$

Commented by ajfour last updated on 28/Jan/20

unfortunately a no solution question, thanks for attempting sir.

$${unfortunately}\:{a}\:{no}\:{solution} \\ $$$${question},\:{thanks}\:{for} \\ $$$${attempting}\:{sir}. \\ $$

Commented by mr W last updated on 28/Jan/20

but it′s again a very challenging question whose solution is not so obvious at first glance. one can really learn through such questions. therefore thanks alot sir!

$${but}\:{it}'{s}\:{again}\:{a}\:{very}\:{challenging}\: \\ $$$${question}\:{whose}\:{solution}\:{is}\:{not}\:{so} \\ $$$${obvious}\:{at}\:{first}\:{glance}.\:{one}\:{can}\:{really} \\ $$$${learn}\:{through}\:{such}\:{questions}. \\ $$$${therefore}\:{thanks}\:{alot}\:{sir}! \\ $$

Commented by john santu last updated on 28/Jan/20

this case closed?

$$\mathrm{this}\:\mathrm{case}\:\mathrm{closed}? \\ $$

Commented by mr W last updated on 28/Jan/20

Commented by mr W last updated on 28/Jan/20

here more explanation why there is no solution for this question. for every point P(h,h^2 ) we can find point A(a,0) and C(0,c) such that A_I =A_(IV) when a=(1+(1/μ))h and c=(1+μ)h^2 . with μ=(((√(10))−1)/3)=constant. for every point P(h,h^2 ) we can find one point B, say B_1 (b_1 ,b_1 ^2 ), such that A_(II) =A_(III) when b_1 =2.581139h (exact value possible) for every point P(h,h^2 ) we can find two points B, say B_2 (b_2 ,b_2 ^2 ) and B_3 (b_3 ,b_3 ^2 ), such that A_(III) =A_(IV) when b_2 =1.471654h (exact value possible) b_3 =6.903689h (exact value possible) we see that we can not select the point P, i.e. find a value for h such that B_1 coincides with B_2 or B_3 , that means it′s impossible to get A_I =A_(II) =A_(III) =A_(IV) .

$${here}\:{more}\:{explanation}\:{why}\:{there}\:{is} \\ $$$${no}\:{solution}\:{for}\:{this}\:{question}. \\ $$$$ \\ $$$${for}\:{every}\:{point}\:{P}\left({h},{h}^{\mathrm{2}} \right)\:{we}\:{can}\:{find} \\ $$$${point}\:{A}\left({a},\mathrm{0}\right)\:{and}\:{C}\left(\mathrm{0},{c}\right)\:{such}\:{that} \\ $$$${A}_{{I}} ={A}_{{IV}} \:{when} \\ $$$${a}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mu}\right){h}\:{and}\:{c}=\left(\mathrm{1}+\mu\right){h}^{\mathrm{2}} . \\ $$$${with}\:\mu=\frac{\sqrt{\mathrm{10}}−\mathrm{1}}{\mathrm{3}}={constant}. \\ $$$$ \\ $$$${for}\:{every}\:{point}\:{P}\left({h},{h}^{\mathrm{2}} \right)\:{we}\:{can}\:{find} \\ $$$${one}\:{point}\:{B},\:{say}\:{B}_{\mathrm{1}} \left({b}_{\mathrm{1}} ,{b}_{\mathrm{1}} ^{\mathrm{2}} \right),\:{such}\:{that} \\ $$$${A}_{{II}} ={A}_{{III}} \:{when} \\ $$$${b}_{\mathrm{1}} =\mathrm{2}.\mathrm{581139}{h}\:\left({exact}\:{value}\:{possible}\right) \\ $$$$ \\ $$$${for}\:{every}\:{point}\:{P}\left({h},{h}^{\mathrm{2}} \right)\:{we}\:{can}\:{find} \\ $$$${two}\:{points}\:{B},\:{say}\:{B}_{\mathrm{2}} \left({b}_{\mathrm{2}} ,{b}_{\mathrm{2}} ^{\mathrm{2}} \right)\:{and} \\ $$$${B}_{\mathrm{3}} \left({b}_{\mathrm{3}} ,{b}_{\mathrm{3}} ^{\mathrm{2}} \right),\:{such}\:{that} \\ $$$${A}_{{III}} ={A}_{{IV}} \:\:{when} \\ $$$${b}_{\mathrm{2}} =\mathrm{1}.\mathrm{471654}{h}\:\left({exact}\:{value}\:{possible}\right) \\ $$$${b}_{\mathrm{3}} =\mathrm{6}.\mathrm{903689}{h}\:\left({exact}\:{value}\:{possible}\right) \\ $$$$ \\ $$$${we}\:{see}\:{that}\:{we}\:{can}\:{not}\:{select}\:{the} \\ $$$${point}\:{P},\:{i}.{e}.\:{find}\:{a}\:{value}\:{for}\:{h}\:{such} \\ $$$${that}\:{B}_{\mathrm{1}} \:{coincides}\:{with}\:{B}_{\mathrm{2}} \:{or}\:{B}_{\mathrm{3}} , \\ $$$${that}\:{means}\:{it}'{s}\:{impossible}\:{to}\:{get} \\ $$$${A}_{{I}} ={A}_{{II}} ={A}_{{III}} ={A}_{{IV}} \:. \\ $$

Commented by mr W last updated on 28/Jan/20

to me the case is clear and closed.

$${to}\:{me}\:{the}\:{case}\:{is}\:{clear}\:{and}\:{closed}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com