
Question and Answers Forum
Question Number 79730 by Henri Boucatchou last updated on 27/Jan/20

Commented by Henri Boucatchou last updated on 27/Jan/20
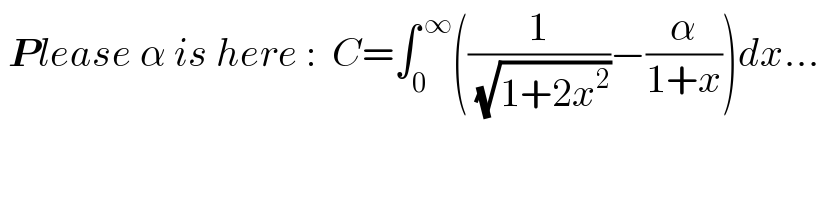
Answered by mind is power last updated on 28/Jan/20
![f(x)=(1/(√(1+2x^2 )))−(1/(1+x)) continus x→∞ f(x)=(((x+1)−(√((1+2x^2 ))))/((x+1)(√(1+2x^2 ))))=((2x−x^2 )/((x+1)(√((1+2x^2 )))(x+1+(√(1+2x^2 ))))) ∼((−x^2 )/(x^3 (√2).(1+(√2))))=−(1/(x(√2)(1+(√2)))) not integrabl in+∞ C diverge a)∫∫_Δ dxdy x∈[−2,2] ∣y∣<2−∣x∣ ⇒∣x∣−2≤y≤2−∣x∣ =∫_(−2) ^2 ∫_(∣x∣−2) ^(2−∣x∣) dxdy =∫_(−2) ^2 [4−2∣x∣]dx =2∫_0 ^2 [4−2x]dx =16−2(4)=8 ∫∫_Δ ((dxdy)/((∣x∣+∣y∣)^2 +4)) we haveΔ=∪_(i=1) ^4 D_i D_1 =(x,y)∣ x+y<2,D_2 x−y<2,D_3 =−x+y<2,D_4 −x−y<2∣ g(x,y)=(1/((∣x∣+∣y∣)^2 +4)) is invsriant in sense g(_− ^+ x,_− ^+ y)=g(x,y) D_1 =ϕ(D_2 )=ϕ′(D_3 )=ϕ′′(D_4 ) ϕ(x,y)=(x,−y) ϕ′(x,y)=(−x,y) ϕ′′(x,y)=(−x,−y) goϕ^i (x,y)=g(x,h),i∈{1,2,3} ⇒∫∫_D_i g(x,y)dxdy=∫∫_D_j g(x,y)dxdy,∀i,j∈{1,2,3,4} ⇒∫∫_Δ g(x,y)dxdy=4∫∫_D_1 g(x,y)dxdy =4∫_0 ^2 ∫_0 ^(2−x) ((dxdy)/((x+y)^2 +4)) ∫_0 ^2 ∫_0 ^(2−x) (dy/(((((x+y)/2))^2 +1)))dx=∫_0 ^2 2∫_0 ^(2−x) (1/2)(dy/(((((x+y)/2))^2 +1))) =∫_0 ^2 2.[tan^(−1) (((x+y)/2))]_0 ^(2−x) ]dx =2∫_0 ^2 ((π/4)−tan^− ((x/2))] by part =π−2∫_0 ^2 tan^(−1) ((x/2))dx=π−2[[_0 ^2 xtan^(−1) ((x/2))]−∫_0 ^2 ((2x)/(1+x^2 ))]dx π−4tan^− (1)+2ln(5)=2ln(5)](Q79796.png)
| ||
Question and Answers Forum | ||
Question Number 79730 by Henri Boucatchou last updated on 27/Jan/20 | ||
 | ||
Commented by Henri Boucatchou last updated on 27/Jan/20 | ||
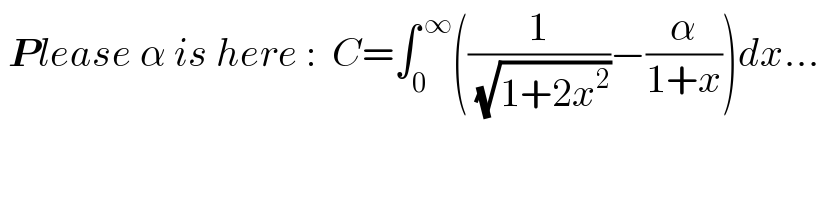 | ||
Answered by mind is power last updated on 28/Jan/20 | ||
![f(x)=(1/(√(1+2x^2 )))−(1/(1+x)) continus x→∞ f(x)=(((x+1)−(√((1+2x^2 ))))/((x+1)(√(1+2x^2 ))))=((2x−x^2 )/((x+1)(√((1+2x^2 )))(x+1+(√(1+2x^2 ))))) ∼((−x^2 )/(x^3 (√2).(1+(√2))))=−(1/(x(√2)(1+(√2)))) not integrabl in+∞ C diverge a)∫∫_Δ dxdy x∈[−2,2] ∣y∣<2−∣x∣ ⇒∣x∣−2≤y≤2−∣x∣ =∫_(−2) ^2 ∫_(∣x∣−2) ^(2−∣x∣) dxdy =∫_(−2) ^2 [4−2∣x∣]dx =2∫_0 ^2 [4−2x]dx =16−2(4)=8 ∫∫_Δ ((dxdy)/((∣x∣+∣y∣)^2 +4)) we haveΔ=∪_(i=1) ^4 D_i D_1 =(x,y)∣ x+y<2,D_2 x−y<2,D_3 =−x+y<2,D_4 −x−y<2∣ g(x,y)=(1/((∣x∣+∣y∣)^2 +4)) is invsriant in sense g(_− ^+ x,_− ^+ y)=g(x,y) D_1 =ϕ(D_2 )=ϕ′(D_3 )=ϕ′′(D_4 ) ϕ(x,y)=(x,−y) ϕ′(x,y)=(−x,y) ϕ′′(x,y)=(−x,−y) goϕ^i (x,y)=g(x,h),i∈{1,2,3} ⇒∫∫_D_i g(x,y)dxdy=∫∫_D_j g(x,y)dxdy,∀i,j∈{1,2,3,4} ⇒∫∫_Δ g(x,y)dxdy=4∫∫_D_1 g(x,y)dxdy =4∫_0 ^2 ∫_0 ^(2−x) ((dxdy)/((x+y)^2 +4)) ∫_0 ^2 ∫_0 ^(2−x) (dy/(((((x+y)/2))^2 +1)))dx=∫_0 ^2 2∫_0 ^(2−x) (1/2)(dy/(((((x+y)/2))^2 +1))) =∫_0 ^2 2.[tan^(−1) (((x+y)/2))]_0 ^(2−x) ]dx =2∫_0 ^2 ((π/4)−tan^− ((x/2))] by part =π−2∫_0 ^2 tan^(−1) ((x/2))dx=π−2[[_0 ^2 xtan^(−1) ((x/2))]−∫_0 ^2 ((2x)/(1+x^2 ))]dx π−4tan^− (1)+2ln(5)=2ln(5)](Q79796.png) | ||
| ||