
Question and Answers Forum
Question Number 79758 by mathmax by abdo last updated on 27/Jan/20
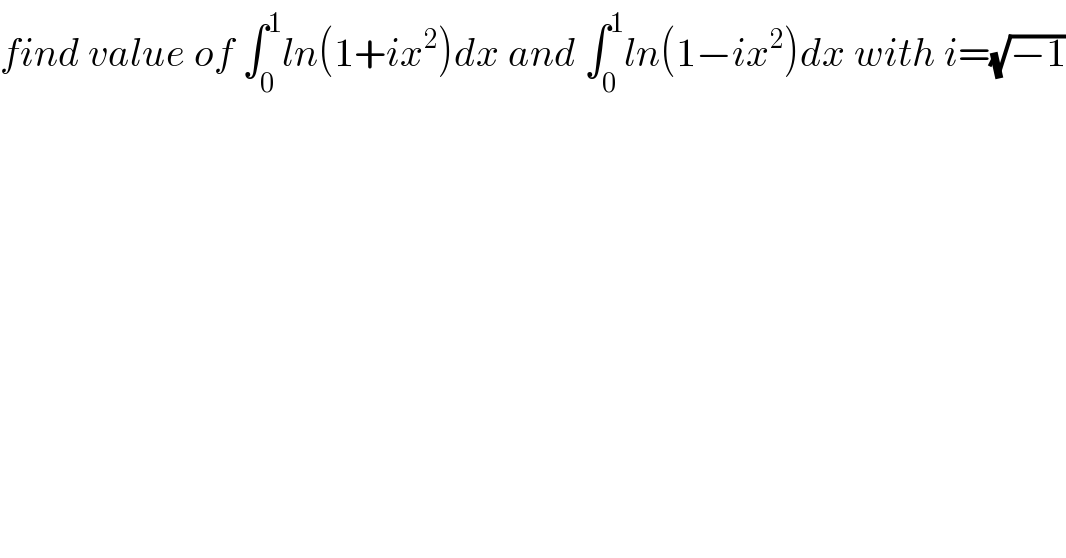
Commented by mathmax by abdo last updated on 29/Jan/20
![let z from C and f(z)=∫_0 ^1 ln(1+zx^2 )dx ⇒ f^′ (z)=∫_0 ^1 (x^2 /(1+zx^2 ))dx =(1/z) ∫_0 ^1 ((zx^2 +1−1)/(1+zx^2 ))dx =(1/z) −(1/z) ∫_0 ^1 (dx/(1+zx^2 )) and ∫_0 ^1 (dx/(1+zx^2 )) =_(x(√z)=t) ∫_0 ^(√z) (dt/((√z)(1+t^2 ))) =(1/(√z)) arctan((√z)) ⇒f^′ (z)=(1/z)−((arctan((√z)))/(z(√z))) ⇒ f(z)=lnz +∫_1 ^z ((arctan((√u)))/(u(√u))) du +c (u=t^2 ) =lnz +∫_1 ^(√z) ((arctan(t))/t^3 )(2t)dt +c =ln(z)+2∫_1 ^(√z) ((arctan(t))/t^2 )dt +c f(1) =∫_0 ^1 ln(1+x^2 )dx =c ⇒ f(z) =lnz +2∫_1 ^(√z) ((arctan(t))/t^2 )dt +∫_0 ^1 ln(1+x^2 )dx we have by parts ∫_1 ^(√z) ((arctan(t))/t^2 )dt =[−((arctant)/t)]_1 ^(√z) +∫_1 ^(√z) (1/(t(1+t^2 )))dt =(π/4)−((arctan((√z)))/(√z)) +∫_1 ^(√z) ((1/t)−(t/(t^2 +1)))dt =(π/4)−((arctan((√z)))/(√z)) +ln((√z))−[(1/2)ln(t^2 +1)]_1 ^(√z) =(π/4)−((arctan((√z)))/(√z)) +(1/2)ln(z)−(1/2){ln(z+1)−ln(2)} ⇒ f(z)=ln(z)+(π/2)−((2arctan((√z)))/(√z)) +ln(z)−ln(z+1)+ln(2)+∫_0 ^1 ln(1+x^2 )dx f(z)=2ln(z)+(π/2) −2((arctan((√z)))/(√z)) −ln(z+1)+ln(2)+∫_0 ^1 ln(1+x^2 )dx by parts ∫_0 ^1 ln(1+x^2 )dx =[xln(1+x^2 )]_0 ^1 −∫_0 ^1 ((2x^2 )/(1+x^2 ))dx =ln(2)−2 ∫_0 ^1 ((1+x^2 −1)/(1+x^2 ))dx =ln(2)−2 +2 ×(π/4) =ln(2)−2+(π/2) ⇒ f(z) =2ln(z) +2ln(2) +π −2 −2((arctan((√z)))/(√z)) −ln(z+1) =∫_0 ^1 ln(1+zx^2 )dx ⇒ ∫_0 ^1 ln(1+ix^2 )dx =f(i) =2ln(i)+2ln(2)+π−2−2 ×((arctan((√i)))/(√i)) −ln(i+1) =2×((iπ)/2) +2ln(2)+π−2 −2 ×((arctan(e^((iπ)/4) ))/e^((iπ)/4) )−ln((√2)e^((iπ)/4) ) =iπ +2ln(2)+π−2 −2e^(−((iπ)/4)) arctan(e^((iπ)/4) )−(1/2)ln(2)−((iπ)/4)](Q79889.png)
| ||
Question and Answers Forum | ||
Question Number 79758 by mathmax by abdo last updated on 27/Jan/20 | ||
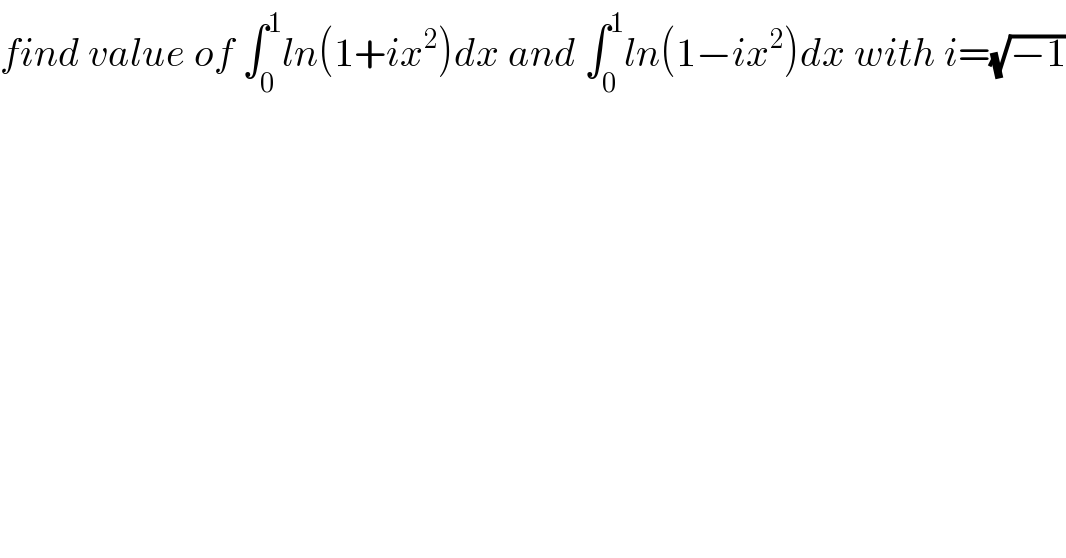 | ||
Commented by mathmax by abdo last updated on 29/Jan/20 | ||
![let z from C and f(z)=∫_0 ^1 ln(1+zx^2 )dx ⇒ f^′ (z)=∫_0 ^1 (x^2 /(1+zx^2 ))dx =(1/z) ∫_0 ^1 ((zx^2 +1−1)/(1+zx^2 ))dx =(1/z) −(1/z) ∫_0 ^1 (dx/(1+zx^2 )) and ∫_0 ^1 (dx/(1+zx^2 )) =_(x(√z)=t) ∫_0 ^(√z) (dt/((√z)(1+t^2 ))) =(1/(√z)) arctan((√z)) ⇒f^′ (z)=(1/z)−((arctan((√z)))/(z(√z))) ⇒ f(z)=lnz +∫_1 ^z ((arctan((√u)))/(u(√u))) du +c (u=t^2 ) =lnz +∫_1 ^(√z) ((arctan(t))/t^3 )(2t)dt +c =ln(z)+2∫_1 ^(√z) ((arctan(t))/t^2 )dt +c f(1) =∫_0 ^1 ln(1+x^2 )dx =c ⇒ f(z) =lnz +2∫_1 ^(√z) ((arctan(t))/t^2 )dt +∫_0 ^1 ln(1+x^2 )dx we have by parts ∫_1 ^(√z) ((arctan(t))/t^2 )dt =[−((arctant)/t)]_1 ^(√z) +∫_1 ^(√z) (1/(t(1+t^2 )))dt =(π/4)−((arctan((√z)))/(√z)) +∫_1 ^(√z) ((1/t)−(t/(t^2 +1)))dt =(π/4)−((arctan((√z)))/(√z)) +ln((√z))−[(1/2)ln(t^2 +1)]_1 ^(√z) =(π/4)−((arctan((√z)))/(√z)) +(1/2)ln(z)−(1/2){ln(z+1)−ln(2)} ⇒ f(z)=ln(z)+(π/2)−((2arctan((√z)))/(√z)) +ln(z)−ln(z+1)+ln(2)+∫_0 ^1 ln(1+x^2 )dx f(z)=2ln(z)+(π/2) −2((arctan((√z)))/(√z)) −ln(z+1)+ln(2)+∫_0 ^1 ln(1+x^2 )dx by parts ∫_0 ^1 ln(1+x^2 )dx =[xln(1+x^2 )]_0 ^1 −∫_0 ^1 ((2x^2 )/(1+x^2 ))dx =ln(2)−2 ∫_0 ^1 ((1+x^2 −1)/(1+x^2 ))dx =ln(2)−2 +2 ×(π/4) =ln(2)−2+(π/2) ⇒ f(z) =2ln(z) +2ln(2) +π −2 −2((arctan((√z)))/(√z)) −ln(z+1) =∫_0 ^1 ln(1+zx^2 )dx ⇒ ∫_0 ^1 ln(1+ix^2 )dx =f(i) =2ln(i)+2ln(2)+π−2−2 ×((arctan((√i)))/(√i)) −ln(i+1) =2×((iπ)/2) +2ln(2)+π−2 −2 ×((arctan(e^((iπ)/4) ))/e^((iπ)/4) )−ln((√2)e^((iπ)/4) ) =iπ +2ln(2)+π−2 −2e^(−((iπ)/4)) arctan(e^((iπ)/4) )−(1/2)ln(2)−((iπ)/4)](Q79889.png) | ||