Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 79807 by Pratah last updated on 28/Jan/20

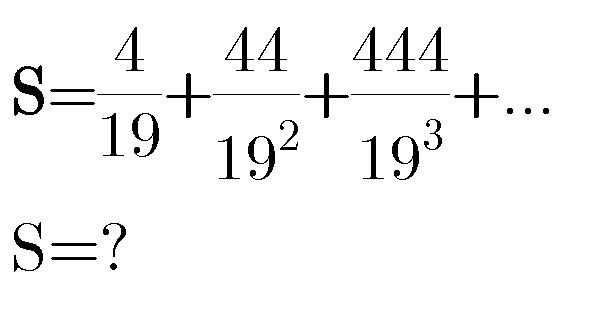
Commented by Pratah last updated on 28/Jan/20

$$\mathrm{thanks}\mathrm{sir}$$

Commented by john santu last updated on 28/Jan/20

$$\mathrm{S}=\frac{4}{19}+\frac{44}{{19}^2}+\frac{444}{{19}^3}+\frac{4444}{{19}^4}+...(\ast )$$$$19\mathrm{S}=4+\frac{44}{19}+\frac{444}{{19}^2}+\frac{4444}{{19}^3}+...(\ast \ast )$$$$(\ast \ast )-(\ast )$$$$18\mathrm{S}=4+4\left(\frac{10}{19}\right)+4\left(\frac{100}{{19}^2}\right)+4\left(\frac{1000}{{19}^3}\right)+...$$$$18\mathrm{S}=4\left(\frac{1}{1-\frac{10}{19}}\right)=\frac{4\times 19}{9}$$$$\mathrm{S}=\frac{38}{81}.$$

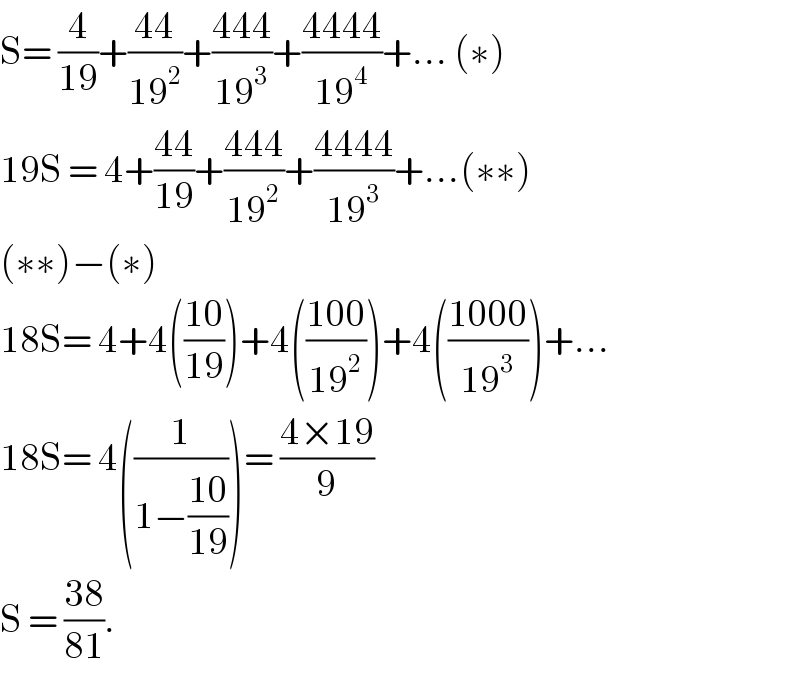
Answered by mr W last updated on 28/Jan/20

$$S=\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{4(1+10+100+...+{10}^{n-1})}{{19}^n}$$$$S=\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{4({10}^n-1)}{9\times {19}^n}$$$$S=\frac{4}{9}\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{{10}^n-1}{{19}^n}$$$$S=\frac{4}{9}\underset{n=1}{\sum ^{\mathrm{\infty }}}[{\left(\frac{10}{19}\right)}^n-{\left(\frac{1}{19}\right)}^n]$$$$S=\frac{4}{9}(\frac{\frac{10}{19}}{1-\frac{10}{19}}-\frac{\frac{1}{19}}{1-\frac{1}{19}})$$$$S=\frac{4}{9}(\frac{10}{9}-\frac{1}{18})$$$$\Rightarrow S=\frac{38}{81}$$

Commented by Pratah last updated on 28/Jan/20

$$\mathrm{thanks}$$

Answered by Smail last updated on 28/Jan/20

$$S=4(\frac{1}{19}+\frac{11}{{19}^2}+\frac{111}{{19}^3}+...)$$$$=4(\frac{1}{19}+\frac{10+1}{{19}^2}+\frac{{10}^2+10+1}{{19}^3}+...)$$$$1+10+{10}^2+...+{10}^n=\frac{1-{10}^{n+1}}{1-10}$$$$S=4(\frac{1-{10}^1}{(1-10)19}+\frac{1-{10}^2}{(1-10){19}^2}+\frac{1-{10}^3}{(1-10){19}^3}+...)$$$$=\frac{4}{1-10}\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{1-{10}^n}{{19}^n}=\frac{4}{9}(\underset{n=1}{\sum ^{\mathrm{\infty }}}{\left(\frac{10}{19}\right)}^n-\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{1}{{19}^n})$$$$=\frac{4}{9}(\frac{10/19}{1-10/19}-\frac{1/19}{1-1/19})$$$$=\frac{4}{9}(\frac{10}{19-10}-\frac{1}{19-1})$$$$S=\frac{38}{81}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com