Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 79816 by jagoll last updated on 28/Jan/20

hello mister. i need help explaining how determine the range of function of rational functions like (i) f(x)=((ax^2 +bx+c)/(px^2 +qx+r)) (ii) f(x)=((ax^2 +bx+c)/(px+q))

$$\mathrm{hello}\:\mathrm{mister}. \\ $$$$\mathrm{i}\:\mathrm{need}\:\mathrm{help}\:\mathrm{explaining}\:\mathrm{how}\:\mathrm{determine} \\ $$$$\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{function} \\ $$$$\mathrm{of}\:\mathrm{rational}\:\mathrm{functions} \\ $$$$\mathrm{like}\:\left(\mathrm{i}\right)\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}}{\mathrm{px}^{\mathrm{2}} +\mathrm{qx}+\mathrm{r}} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}}{\mathrm{px}+\mathrm{q}} \\ $$

Answered by MJS last updated on 28/Jan/20

y=((ax^2 +bx+c)/(px^2 +qx+r)) leads to x^2 +((qy−b)/(py−a))+((ry−c)/(py−a))=0 D=(((4pr−q^2 )y^2 −2(2ar−bq+2cp)y+4ac−b^2 )/(4(py−a)^2 )) D<0 ⇒ no real solution for x ⇒ no y exists the range then is R\[interval for y where D<0] same when p=0 which is your (ii)

$${y}=\frac{{ax}^{\mathrm{2}} +{bx}+{c}}{{px}^{\mathrm{2}} +{qx}+{r}} \\ $$$$\mathrm{leads}\:\mathrm{to} \\ $$$${x}^{\mathrm{2}} +\frac{{qy}−{b}}{{py}−{a}}+\frac{{ry}−{c}}{{py}−{a}}=\mathrm{0} \\ $$$${D}=\frac{\left(\mathrm{4}{pr}−{q}^{\mathrm{2}} \right){y}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}{ar}−{bq}+\mathrm{2}{cp}\right){y}+\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}\left({py}−{a}\right)^{\mathrm{2}} } \\ $$$${D}<\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{for}\:{x}\:\Rightarrow\:\mathrm{no}\:{y}\:\mathrm{exists} \\ $$$$\mathrm{the}\:\mathrm{range}\:\mathrm{then}\:\mathrm{is}\:\mathbb{R}\backslash\left[\mathrm{interval}\:\mathrm{for}\:{y}\:\mathrm{where}\:{D}<\mathrm{0}\right] \\ $$$$\mathrm{same}\:\mathrm{when}\:{p}=\mathrm{0}\:\mathrm{which}\:\mathrm{is}\:\mathrm{your}\:\left(\mathrm{ii}\right) \\ $$

Commented by jagoll last updated on 28/Jan/20

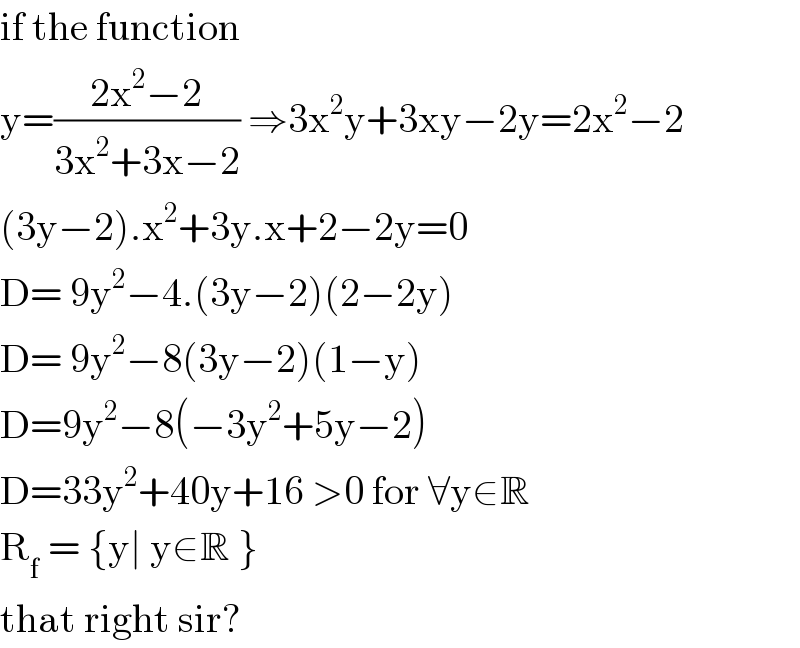
if the function y=((2x^2 −2)/(3x^2 +3x−2)) ⇒3x^2 y+3xy−2y=2x^2 −2 (3y−2).x^2 +3y.x+2−2y=0 D= 9y^2 −4.(3y−2)(2−2y) D= 9y^2 −8(3y−2)(1−y) D=9y^2 −8(−3y^2 +5y−2) D=33y^2 +40y+16 >0 for ∀y∈R R_f = {y∣ y∈R } that right sir?

$$\mathrm{if}\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{y}=\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{3x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}}\:\Rightarrow\mathrm{3x}^{\mathrm{2}} \mathrm{y}+\mathrm{3xy}−\mathrm{2y}=\mathrm{2x}^{\mathrm{2}} −\mathrm{2} \\ $$$$\left(\mathrm{3y}−\mathrm{2}\right).\mathrm{x}^{\mathrm{2}} +\mathrm{3y}.\mathrm{x}+\mathrm{2}−\mathrm{2y}=\mathrm{0} \\ $$$$\mathrm{D}=\:\mathrm{9y}^{\mathrm{2}} −\mathrm{4}.\left(\mathrm{3y}−\mathrm{2}\right)\left(\mathrm{2}−\mathrm{2y}\right) \\ $$$$\mathrm{D}=\:\mathrm{9y}^{\mathrm{2}} −\mathrm{8}\left(\mathrm{3y}−\mathrm{2}\right)\left(\mathrm{1}−\mathrm{y}\right) \\ $$$$\mathrm{D}=\mathrm{9y}^{\mathrm{2}} −\mathrm{8}\left(−\mathrm{3y}^{\mathrm{2}} +\mathrm{5y}−\mathrm{2}\right) \\ $$$$\mathrm{D}=\mathrm{33y}^{\mathrm{2}} +\mathrm{40y}+\mathrm{16}\:>\mathrm{0}\:\mathrm{for}\:\forall\mathrm{y}\in\mathbb{R} \\ $$$$\mathrm{R}_{\mathrm{f}} \:=\:\left\{\mathrm{y}\mid\:\mathrm{y}\in\mathbb{R}\:\right\} \\ $$$$\mathrm{that}\:\mathrm{right}\:\mathrm{sir}? \\ $$

Commented by jagoll last updated on 28/Jan/20

range function not related to flat asymtot sir?

$$\mathrm{range}\:\mathrm{function}\:\mathrm{not}\:\mathrm{related}\:\mathrm{to} \\ $$$$\mathrm{flat}\:\mathrm{asymtot}\:\mathrm{sir}? \\ $$

Commented by jagoll last updated on 28/Jan/20

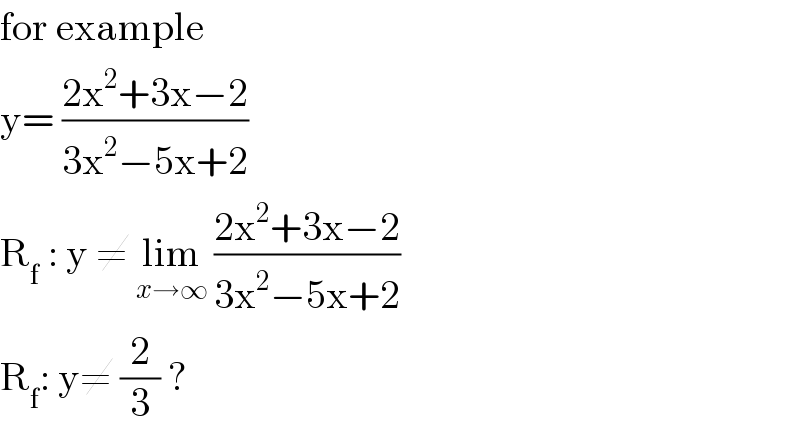
for example y= ((2x^2 +3x−2)/(3x^2 −5x+2)) R_f : y ≠ lim_(x→∞) ((2x^2 +3x−2)/(3x^2 −5x+2)) R_f : y≠ (2/3) ?

$$\mathrm{for}\:\mathrm{example}\: \\ $$$$\mathrm{y}=\:\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}}{\mathrm{3x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{2}} \\ $$$$\mathrm{R}_{\mathrm{f}} \::\:\mathrm{y}\:\neq\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}}{\mathrm{3x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{2}} \\ $$$$\mathrm{R}_{\mathrm{f}} :\:\mathrm{y}\neq\:\frac{\mathrm{2}}{\mathrm{3}}\:? \\ $$

Commented by MJS last updated on 28/Jan/20

y=((2x^2 −2)/(3x^2 +3x−2)) x^2 +((3y)/(3y−2))x−((2(y−1))/(3y−2))=0 [x^2 +Px+Q=0 ⇒ D=(P^2 /4)−Q] D=((33y^2 −40y+16)/(4(3y−2)^2 ))>0∀y∈R ⇒ range is R

$${y}=\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{3}{y}}{\mathrm{3}{y}−\mathrm{2}}{x}−\frac{\mathrm{2}\left({y}−\mathrm{1}\right)}{\mathrm{3}{y}−\mathrm{2}}=\mathrm{0} \\ $$$$\:\:\:\:\:\left[{x}^{\mathrm{2}} +{Px}+{Q}=\mathrm{0}\:\Rightarrow\:{D}=\frac{{P}^{\mathrm{2}} }{\mathrm{4}}−{Q}\right] \\ $$$${D}=\frac{\mathrm{33}{y}^{\mathrm{2}} −\mathrm{40}{y}+\mathrm{16}}{\mathrm{4}\left(\mathrm{3}{y}−\mathrm{2}\right)^{\mathrm{2}} }>\mathrm{0}\forall{y}\in\mathbb{R} \\ $$$$\Rightarrow\:\mathrm{range}\:\mathrm{is}\:\mathbb{R} \\ $$

Commented by MJS last updated on 28/Jan/20

y=((2x^2 +3x−2)/(3x^2 −5x+2)) x^2 −((5y+3)/(3y−2))x+((2(y+1))/(3y−2))=0 D=((y^2 +22y+25)/(4(3y−2)^2 )) D<0 for −11−4(√6)<y<−11+4(√6) ⇒ range is R\]−11−4(√6); −11+4(√6)[

$${y}=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{5}{y}+\mathrm{3}}{\mathrm{3}{y}−\mathrm{2}}{x}+\frac{\mathrm{2}\left({y}+\mathrm{1}\right)}{\mathrm{3}{y}−\mathrm{2}}=\mathrm{0} \\ $$$${D}=\frac{{y}^{\mathrm{2}} +\mathrm{22}{y}+\mathrm{25}}{\mathrm{4}\left(\mathrm{3}{y}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${D}<\mathrm{0}\:\mathrm{for}\:−\mathrm{11}−\mathrm{4}\sqrt{\mathrm{6}}<{y}<−\mathrm{11}+\mathrm{4}\sqrt{\mathrm{6}} \\ $$$$\left.\Rightarrow\:\mathrm{range}\:\mathrm{is}\:\mathbb{R}\backslash\right]−\mathrm{11}−\mathrm{4}\sqrt{\mathrm{6}};\:−\mathrm{11}+\mathrm{4}\sqrt{\mathrm{6}}\left[\right. \\ $$

Commented by jagoll last updated on 28/Jan/20

sir how to get in line 2? still understand

$$\mathrm{sir}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{in}\:\mathrm{line}\:\mathrm{2}?\:\mathrm{still}\:\mathrm{understand} \\ $$

Commented by jagoll last updated on 28/Jan/20

3x^2 y+3xy−2y−2x^2 +2=0 (3y−2)x^2 +(3y)x+2−2y=0 x^2 +((3y)/(3y−2)) x+((2(1−y))/(3y−2))=0 that right sir?

$$\mathrm{3x}^{\mathrm{2}} \mathrm{y}+\mathrm{3xy}−\mathrm{2y}−\mathrm{2x}^{\mathrm{2}} +\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{3y}−\mathrm{2}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{3y}\right)\mathrm{x}+\mathrm{2}−\mathrm{2y}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{3y}}{\mathrm{3y}−\mathrm{2}}\:\mathrm{x}+\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{y}\right)}{\mathrm{3y}−\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{that}\:\mathrm{right}\:\mathrm{sir}? \\ $$

Commented by MJS last updated on 28/Jan/20

y=((2x^2 +3x−2)/(3x^2 −5x+2)) (3x^2 −5x+2)y=2x^2 +3x−2 (3y−2)x^2 −(5y+3)x+2(y+1)=0 x^2 −((5y+3)/(3y−2))x+((2(y+1))/(3y−2))=0 you′ve made mistakes in line 1 p=−((5y+3)/(3y−2)); q=((2(y+1))/(3y−2)) D=(p^2 /4)−q=((y^2 +22y+25)/(4(3y−2)^2 ))

$${y}=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}} \\ $$$$\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}\right){y}=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2} \\ $$$$\left(\mathrm{3}{y}−\mathrm{2}\right){x}^{\mathrm{2}} −\left(\mathrm{5}{y}+\mathrm{3}\right){x}+\mathrm{2}\left({y}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{5}{y}+\mathrm{3}}{\mathrm{3}{y}−\mathrm{2}}{x}+\frac{\mathrm{2}\left({y}+\mathrm{1}\right)}{\mathrm{3}{y}−\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{you}'\mathrm{ve}\:\mathrm{made}\:\mathrm{mistakes}\:\mathrm{in}\:\mathrm{line}\:\mathrm{1} \\ $$$$ \\ $$$${p}=−\frac{\mathrm{5}{y}+\mathrm{3}}{\mathrm{3}{y}−\mathrm{2}};\:{q}=\frac{\mathrm{2}\left({y}+\mathrm{1}\right)}{\mathrm{3}{y}−\mathrm{2}} \\ $$$${D}=\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}=\frac{{y}^{\mathrm{2}} +\mathrm{22}{y}+\mathrm{25}}{\mathrm{4}\left(\mathrm{3}{y}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$

Commented by MJS last updated on 29/Jan/20

look at qu. 79883

$$\mathrm{look}\:\mathrm{at}\:\mathrm{qu}.\:\mathrm{79883} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com