
Question and Answers Forum
Question Number 79876 by mathocean1 last updated on 28/Jan/20
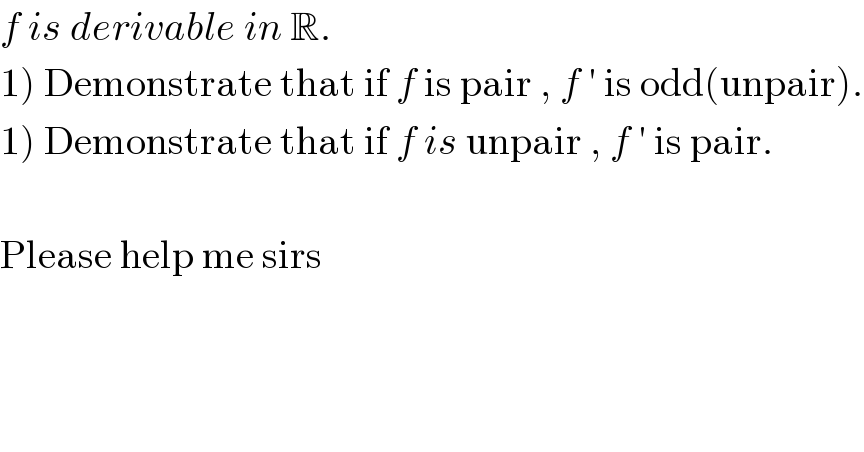
Commented by MJS last updated on 29/Jan/20
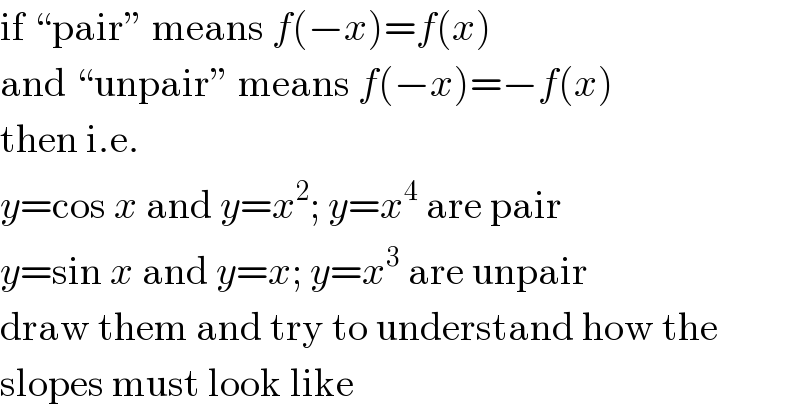
Answered by Henri Boucatchou last updated on 29/Jan/20
![f is derivable for all x_0 ∈R, that′s lim_(x→x_0 ) ((f(x)−f(x_0 ))/(x−x_0 ))=f ′(x_0 ) f pair ⇒ lim_(x−→x_0 ) −((f(−x)−f(−x_0 ))/((−x)−(−x_0 )))=−f ′(−x_0 )=lim_(x→x_0 ) ((f(x)−f(x_0 ))/(x−x_0 ))=f ′(x_0 ) ⇒ f ′(−x_0 )=−f ′(x_0 ) e.i. f ′ is odd; f unpair ⇒ lim_(x→x_0 ) −((f(−x)−f(−x_0 ))/((−x)−(−x_0 )))=−f ′(−x_0 )=lim_(x→x_0 ) ((−[f(x)−f(x_0 )])/(x−x_0 ))=−f ′(x_0 ) ⇒−f ′(−x_0 )=−f ′(x_0 ) ⇒ f ′(−x_0 )=f ′(x_0 ) e.i. f ′ is pair.](Q79912.png)
| ||
Question and Answers Forum | ||
Question Number 79876 by mathocean1 last updated on 28/Jan/20 | ||
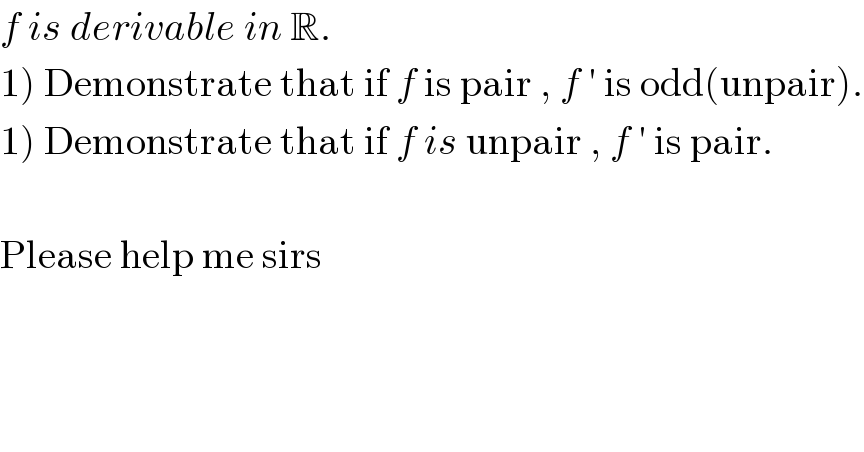 | ||
Commented by MJS last updated on 29/Jan/20 | ||
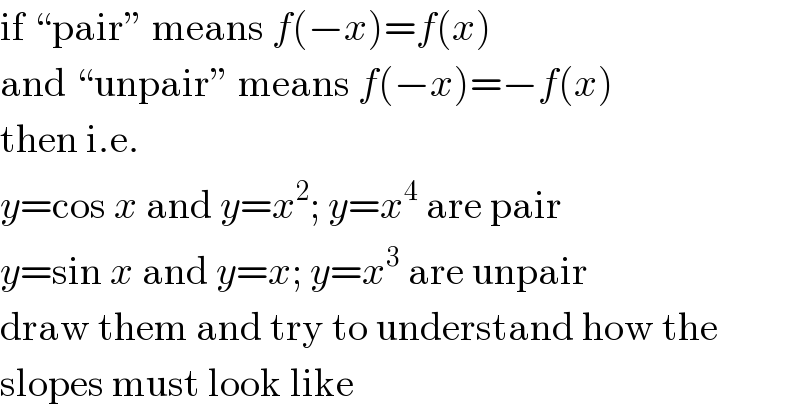 | ||
Answered by Henri Boucatchou last updated on 29/Jan/20 | ||
![f is derivable for all x_0 ∈R, that′s lim_(x→x_0 ) ((f(x)−f(x_0 ))/(x−x_0 ))=f ′(x_0 ) f pair ⇒ lim_(x−→x_0 ) −((f(−x)−f(−x_0 ))/((−x)−(−x_0 )))=−f ′(−x_0 )=lim_(x→x_0 ) ((f(x)−f(x_0 ))/(x−x_0 ))=f ′(x_0 ) ⇒ f ′(−x_0 )=−f ′(x_0 ) e.i. f ′ is odd; f unpair ⇒ lim_(x→x_0 ) −((f(−x)−f(−x_0 ))/((−x)−(−x_0 )))=−f ′(−x_0 )=lim_(x→x_0 ) ((−[f(x)−f(x_0 )])/(x−x_0 ))=−f ′(x_0 ) ⇒−f ′(−x_0 )=−f ′(x_0 ) ⇒ f ′(−x_0 )=f ′(x_0 ) e.i. f ′ is pair.](Q79912.png) | ||
| ||