Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 79883 by MJS last updated on 29/Jan/20

to Sir Jagoll (and of course everybody else) (1) y=((x^2 −x−6)/(x^2 −3x−4))= =(((x−3)(x+2))/((x−4)(x+1))) ⇒ ⇒ { ((zeros at x=−2; x=3)),((vertical asymptotes at x=−1; x=4)) :} defined for x∈R\{−1; 4} range: transforming y=((x^2 −x−6)/(x^2 −3x−4)) to x^2 −((3y−1)/(y−1))x−((2(2y−3))/(y−1))=0 D=((25y^2 −46y+25)/(4(y−1)^2 ))>0∀x∈R ⇒ ⇒ { ((range=R)),((horizontal asymptote at y=1 (∗))) :} (∗) doesn′t mean y=1 is not within range!!! x=1 ⇒ y=1 y′=−((2(x^2 −2x+7))/((x−4)^2 (x+1)^2 )) no real zeros ⇒ ⇒ no local extremes y′′=((4(x^3 −3x^2 +21x−25))/((x−4)^3 (x+1)^3 ))=0 at x≈1.33131 ⇒ ⇒ turning point (2) y=((x^2 −x−6)/(x^2 −3x+4))= =(((x−3)(x+2))/(x^2 −3x+4)); x^2 −3x+4=0 no real zeros ⇒ ⇒ { ((zeros at x=−2; x=3)),((no vertical asymptote)) :} defined for x∈R range: transforming y=((x^2 −x−6)/(x^2 −3x+4)) to x^2 −((3y−1)/(y−1))x+((2(2y+3))/(y−1))=0 D=−((7y^2 +14y−25)/(4(y−1)^2 ))≥0 for −1−((4(√(14)))/7)≤y≤−1+((4(√(14)))/7) ⇒ ⇒ { ((range=[−1−((4(√(14)))/7); −1+((4(√(14)))/7)])),((horizontal asymptote at y=1 (∗))) :} (∗) doesn′t mean y=1 is not within range!!! x=5 ⇒ y=1 y′=−((2(x^2 −10x+11))/((x^2 −3x+4)^2 ))=0 at x=5±(√(14)) y^(′′) =((4(x^3 −15x^2 +33x−13))/((x^2 −3x+4)^3 )) y′′ { ((>0 at x=5−(√(14)) ⇒ local minimum)),((<0 at x=5+(√(14)) ⇒ local maximum)),((=0 at { ((x≈.506699)),((x≈2.06421)),((x≈12.4291)) :} ⇒ 3 turning points )) :} (3) y=((x^2 −x+6)/(x^2 −3x−4))= =((x^2 −x+6)/((x−4)(x+1))) ⇒ ⇒ { ((no real zeros)),((vertical asymptotes at x=−1; x=4)) :} defined for x∈R\{−1; 4} range: transforming y=((x^2 −x+6)/(x^2 −3x−4)) to x^2 −((3y−1)/(y−1))x−((2(2y+3))/(y−1))=0 D=((25y^2 +2y−23)/(4(y−1)^2 ))<0 for −1<y<((23)/(25)) ⇒ ⇒ { ((range=R\]−1; ((23)/(25))[)),((horizontal asymptote at y=1 (∗))) :} (∗) doesn′t mean y=1 is not within range!!! x=−5 ⇒ y=1 y′=−((2(x^2 +10x−11))/((x−4)^2 (x+1)^2 ))=0 at x=−11; x=1 y′′=((4(x^3 +15x^2 −33x+53))/((x−4)^3 (x+1)^3 )) y′′ { ((>0 at x=−11 ⇒ local minimum)),((<0 at x=1 ⇒ local maximum)),((=0 at x≈−17.1098 ⇒ turning point)) :}

$$\mathrm{to}\:\mathrm{Sir}\:\mathrm{Jagoll}\:\left({and}\:{of}\:{course}\:{everybody}\:{else}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right) \\ $$$${y}=\frac{{x}^{\mathrm{2}} −{x}−\mathrm{6}}{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}}= \\ $$$$=\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{2}\right)}{\left({x}−\mathrm{4}\right)\left({x}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{zeros}\:\mathrm{at}\:{x}=−\mathrm{2};\:{x}=\mathrm{3}}\\{\mathrm{vertical}\:\mathrm{asymptotes}\:\mathrm{at}\:{x}=−\mathrm{1};\:{x}=\mathrm{4}}\end{cases} \\ $$$$\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{R}\backslash\left\{−\mathrm{1};\:\mathrm{4}\right\} \\ $$$$\mathrm{range}:\:\mathrm{transforming}\:{y}=\frac{{x}^{\mathrm{2}} −{x}−\mathrm{6}}{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}}\:\mathrm{to} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{3}{y}−\mathrm{1}}{{y}−\mathrm{1}}{x}−\frac{\mathrm{2}\left(\mathrm{2}{y}−\mathrm{3}\right)}{{y}−\mathrm{1}}=\mathrm{0} \\ $$$${D}=\frac{\mathrm{25}{y}^{\mathrm{2}} −\mathrm{46}{y}+\mathrm{25}}{\mathrm{4}\left({y}−\mathrm{1}\right)^{\mathrm{2}} }>\mathrm{0}\forall{x}\in\mathbb{R}\:\Rightarrow \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{range}=\mathbb{R}}\\{\mathrm{horizontal}\:\mathrm{asymptote}\:\mathrm{at}\:{y}=\mathrm{1}\:\left(\ast\right)}\end{cases} \\ $$$$\left(\ast\right)\:\mathrm{doesn}'\mathrm{t}\:\mathrm{mean}\:{y}=\mathrm{1}\:\mathrm{is}\:\mathrm{not}\:\mathrm{within}\:\mathrm{range}!!! \\ $$$$\:\:\:\:\:\:\:\:{x}=\mathrm{1}\:\Rightarrow\:{y}=\mathrm{1} \\ $$$${y}'=−\frac{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{7}\right)}{\left({x}−\mathrm{4}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{no}\:\mathrm{real}\:\mathrm{zeros}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{local}\:\mathrm{extremes} \\ $$$${y}''=\frac{\mathrm{4}\left({x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{21}{x}−\mathrm{25}\right)}{\left({x}−\mathrm{4}\right)^{\mathrm{3}} \left({x}+\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{0}\:\mathrm{at}\:{x}\approx\mathrm{1}.\mathrm{33131}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{turning}\:\mathrm{point} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${y}=\frac{{x}^{\mathrm{2}} −{x}−\mathrm{6}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}}= \\ $$$$=\frac{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{2}\right)}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}};\:{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}=\mathrm{0}\:\mathrm{no}\:\mathrm{real}\:\mathrm{zeros}\:\Rightarrow \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{zeros}\:\mathrm{at}\:{x}=−\mathrm{2};\:{x}=\mathrm{3}}\\{\mathrm{no}\:\mathrm{vertical}\:\mathrm{asymptote}}\end{cases} \\ $$$$\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{R} \\ $$$$\mathrm{range}:\:\mathrm{transforming}\:{y}=\frac{{x}^{\mathrm{2}} −{x}−\mathrm{6}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}}\:\mathrm{to} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{3}{y}−\mathrm{1}}{{y}−\mathrm{1}}{x}+\frac{\mathrm{2}\left(\mathrm{2}{y}+\mathrm{3}\right)}{{y}−\mathrm{1}}=\mathrm{0} \\ $$$${D}=−\frac{\mathrm{7}{y}^{\mathrm{2}} +\mathrm{14}{y}−\mathrm{25}}{\mathrm{4}\left({y}−\mathrm{1}\right)^{\mathrm{2}} }\geqslant\mathrm{0}\:\mathrm{for}\:−\mathrm{1}−\frac{\mathrm{4}\sqrt{\mathrm{14}}}{\mathrm{7}}\leqslant{y}\leqslant−\mathrm{1}+\frac{\mathrm{4}\sqrt{\mathrm{14}}}{\mathrm{7}}\:\Rightarrow \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{range}=\left[−\mathrm{1}−\frac{\mathrm{4}\sqrt{\mathrm{14}}}{\mathrm{7}};\:−\mathrm{1}+\frac{\mathrm{4}\sqrt{\mathrm{14}}}{\mathrm{7}}\right]}\\{\mathrm{horizontal}\:\mathrm{asymptote}\:\mathrm{at}\:{y}=\mathrm{1}\:\left(\ast\right)}\end{cases} \\ $$$$\left(\ast\right)\:\mathrm{doesn}'\mathrm{t}\:\mathrm{mean}\:{y}=\mathrm{1}\:\mathrm{is}\:\mathrm{not}\:\mathrm{within}\:\mathrm{range}!!! \\ $$$$\:\:\:\:\:\:\:\:{x}=\mathrm{5}\:\Rightarrow\:{y}=\mathrm{1} \\ $$$${y}'=−\frac{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{11}\right)}{\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}\right)^{\mathrm{2}} }=\mathrm{0}\:\mathrm{at}\:{x}=\mathrm{5}\pm\sqrt{\mathrm{14}} \\ $$$${y}^{''} =\frac{\mathrm{4}\left({x}^{\mathrm{3}} −\mathrm{15}{x}^{\mathrm{2}} +\mathrm{33}{x}−\mathrm{13}\right)}{\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}\right)^{\mathrm{3}} } \\ $$$${y}''\begin{cases}{>\mathrm{0}\:\mathrm{at}\:{x}=\mathrm{5}−\sqrt{\mathrm{14}}\:\Rightarrow\:\mathrm{local}\:\mathrm{minimum}}\\{<\mathrm{0}\:\mathrm{at}\:{x}=\mathrm{5}+\sqrt{\mathrm{14}}\:\Rightarrow\:\mathrm{local}\:\mathrm{maximum}}\\{=\mathrm{0}\:\mathrm{at}\:\begin{cases}{{x}\approx.\mathrm{506699}}\\{{x}\approx\mathrm{2}.\mathrm{06421}}\\{{x}\approx\mathrm{12}.\mathrm{4291}}\end{cases}\:\Rightarrow\:\mathrm{3}\:\mathrm{turning}\:\mathrm{points}\:}\end{cases} \\ $$$$ \\ $$$$\left(\mathrm{3}\right) \\ $$$${y}=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{6}}{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}}= \\ $$$$=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{6}}{\left({x}−\mathrm{4}\right)\left({x}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{no}\:\mathrm{real}\:\mathrm{zeros}}\\{\mathrm{vertical}\:\mathrm{asymptotes}\:\mathrm{at}\:{x}=−\mathrm{1};\:{x}=\mathrm{4}}\end{cases} \\ $$$$\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{R}\backslash\left\{−\mathrm{1};\:\mathrm{4}\right\} \\ $$$$\mathrm{range}:\:\mathrm{transforming}\:{y}=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{6}}{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}}\:\mathrm{to} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{3}{y}−\mathrm{1}}{{y}−\mathrm{1}}{x}−\frac{\mathrm{2}\left(\mathrm{2}{y}+\mathrm{3}\right)}{{y}−\mathrm{1}}=\mathrm{0} \\ $$$${D}=\frac{\mathrm{25}{y}^{\mathrm{2}} +\mathrm{2}{y}−\mathrm{23}}{\mathrm{4}\left({y}−\mathrm{1}\right)^{\mathrm{2}} }<\mathrm{0}\:\mathrm{for}\:−\mathrm{1}<{y}<\frac{\mathrm{23}}{\mathrm{25}}\:\Rightarrow \\ $$$$\Rightarrow\:\begin{cases}{\left.\mathrm{range}=\mathbb{R}\backslash\right]−\mathrm{1};\:\frac{\mathrm{23}}{\mathrm{25}}\left[\right.}\\{\mathrm{horizontal}\:\mathrm{asymptote}\:\mathrm{at}\:{y}=\mathrm{1}\:\left(\ast\right)}\end{cases} \\ $$$$\left(\ast\right)\:\mathrm{doesn}'\mathrm{t}\:\mathrm{mean}\:{y}=\mathrm{1}\:\mathrm{is}\:\mathrm{not}\:\mathrm{within}\:\mathrm{range}!!! \\ $$$$\:\:\:\:\:\:\:\:{x}=−\mathrm{5}\:\Rightarrow\:{y}=\mathrm{1} \\ $$$${y}'=−\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{11}\right)}{\left({x}−\mathrm{4}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0}\:\mathrm{at}\:{x}=−\mathrm{11};\:{x}=\mathrm{1} \\ $$$${y}''=\frac{\mathrm{4}\left({x}^{\mathrm{3}} +\mathrm{15}{x}^{\mathrm{2}} −\mathrm{33}{x}+\mathrm{53}\right)}{\left({x}−\mathrm{4}\right)^{\mathrm{3}} \left({x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${y}''\begin{cases}{>\mathrm{0}\:\mathrm{at}\:{x}=−\mathrm{11}\:\Rightarrow\:\mathrm{local}\:\mathrm{minimum}}\\{<\mathrm{0}\:\mathrm{at}\:{x}=\mathrm{1}\:\Rightarrow\:\mathrm{local}\:\mathrm{maximum}}\\{=\mathrm{0}\:\mathrm{at}\:{x}\approx−\mathrm{17}.\mathrm{1098}\:\Rightarrow\:\mathrm{turning}\:\mathrm{point}}\end{cases} \\ $$

Commented by TawaTawa last updated on 29/Jan/20

Thanks for your time sir, God bless you.

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Commented by jagoll last updated on 29/Jan/20

waw...thank you mister. i was confused, my teacher said that horizontal asymptotes were not include in the range.

$$\mathrm{waw}...\mathrm{thank}\:\mathrm{you}\:\mathrm{mister}.\:\mathrm{i}\:\mathrm{was}\: \\ $$$$\mathrm{confused},\:\mathrm{my}\:\mathrm{teacher}\:\mathrm{said}\:\mathrm{that}\:\mathrm{horizontal} \\ $$$$\mathrm{asymptotes}\:\mathrm{were}\:\mathrm{not}\:\mathrm{include}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{range}. \\ $$

Commented by jagoll last updated on 29/Jan/20

mr. if given function y= ((ax+b)/(cx+d )) , is it true that the range is not the same as the horizontal asymptote? R_f : y ≠ (a/c) ?

$$\mathrm{mr}.\:\mathrm{if}\:\mathrm{given}\:\mathrm{function}\: \\ $$$$\mathrm{y}=\:\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{cx}+\mathrm{d}\:}\:,\:\mathrm{is}\:\mathrm{it}\:\mathrm{true}\:\mathrm{that}\:\mathrm{the}\:\mathrm{range} \\ $$$$\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{horizontal} \\ $$$$\mathrm{asymptote}?\: \\ $$$$\mathrm{R}_{\mathrm{f}} \::\:\mathrm{y}\:\neq\:\frac{\mathrm{a}}{\mathrm{c}}\:? \\ $$

Commented by john santu last updated on 29/Jan/20

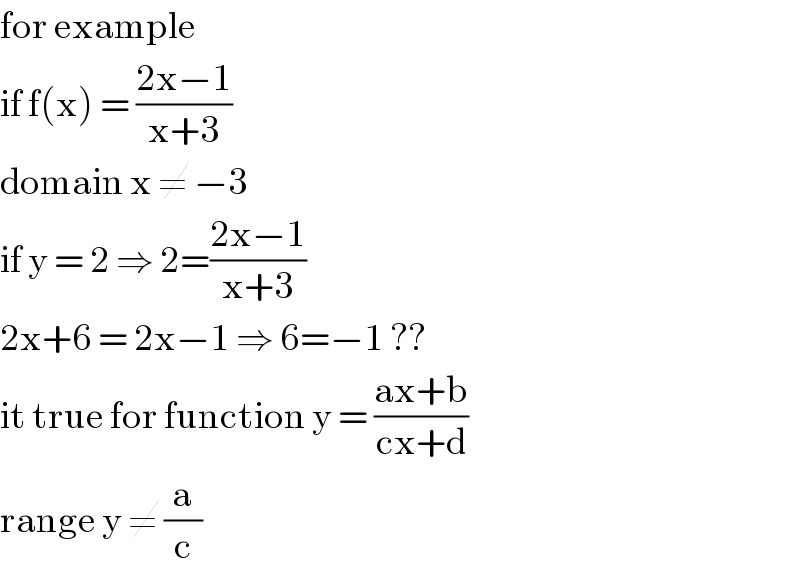
for example if f(x) = ((2x−1)/(x+3)) domain x ≠ −3 if y = 2 ⇒ 2=((2x−1)/(x+3)) 2x+6 = 2x−1 ⇒ 6=−1 ?? it true for function y = ((ax+b)/(cx+d)) range y ≠ (a/c)

$$\mathrm{for}\:\mathrm{example}\: \\ $$$$\mathrm{if}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{x}+\mathrm{3}}\: \\ $$$$\mathrm{domain}\:\mathrm{x}\:\neq\:−\mathrm{3}\: \\ $$$$\mathrm{if}\:\mathrm{y}\:=\:\mathrm{2}\:\Rightarrow\:\mathrm{2}=\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{x}+\mathrm{3}} \\ $$$$\mathrm{2x}+\mathrm{6}\:=\:\mathrm{2x}−\mathrm{1}\:\Rightarrow\:\mathrm{6}=−\mathrm{1}\:?? \\ $$$$\mathrm{it}\:\mathrm{true}\:\mathrm{for}\:\mathrm{function}\:\mathrm{y}\:=\:\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{cx}+\mathrm{d}} \\ $$$$\mathrm{range}\:\mathrm{y}\:\neq\:\frac{\mathrm{a}}{\mathrm{c}} \\ $$

Commented by jagoll last updated on 29/Jan/20

thanks sir

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 29/Jan/20

y=((ax+b)/(cx+d)) ⇒ { ((zero at x=−(b/a))),((vertical asymptote at x=−(d/c) )) :} defined for x∈R\{−(d/c)} y=((ax+b)/(cx+d)) ⇔ x=−((dy−b)/(cy−a)) ⇒ range=R\{(a/c)} horizontal asymptote at y=(a/c) so you are right

$${y}=\frac{{ax}+{b}}{{cx}+{d}}\:\Rightarrow\:\begin{cases}{\mathrm{zero}\:\mathrm{at}\:{x}=−\frac{{b}}{{a}}}\\{\mathrm{vertical}\:\mathrm{asymptote}\:\mathrm{at}\:{x}=−\frac{{d}}{{c}}\:}\end{cases} \\ $$$$\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{R}\backslash\left\{−\frac{{d}}{{c}}\right\} \\ $$$${y}=\frac{{ax}+{b}}{{cx}+{d}}\:\Leftrightarrow\:{x}=−\frac{{dy}−{b}}{{cy}−{a}}\:\Rightarrow\:\mathrm{range}=\mathbb{R}\backslash\left\{\frac{{a}}{{c}}\right\} \\ $$$$\mathrm{horizontal}\:\mathrm{asymptote}\:\mathrm{at}\:{y}=\frac{{a}}{{c}} \\ $$$$\mathrm{so}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$

Commented by jagoll last updated on 29/Jan/20

sir your notation is ]14−4(√(6 )) ; 14+4(√6) [ it same as y ≤ 14−4(√6) ∨y ≥ 14+4(√6) ?

$$\mathrm{sir}\:\mathrm{your}\:\mathrm{notation}\:\mathrm{is} \\ $$$$\left.\right]\mathrm{14}−\mathrm{4}\sqrt{\mathrm{6}\:}\:;\:\mathrm{14}+\mathrm{4}\sqrt{\mathrm{6}}\:\left[\:\right. \\ $$$$\mathrm{it}\:\mathrm{same}\:\mathrm{as}\:\mathrm{y}\:\leqslant\:\mathrm{14}−\mathrm{4}\sqrt{\mathrm{6}}\:\vee\mathrm{y}\:\geqslant\:\mathrm{14}+\mathrm{4}\sqrt{\mathrm{6}} \\ $$$$? \\ $$

Commented by MJS last updated on 29/Jan/20

depends... y∈[a; b] is the same as a≤y≤b ⇒ y∈R\[a; b] means y<a∨y>b y∈]a; b[ is the same as a<y<b ⇒ y∈R\]a; b[ means y≤a∨y≥b

$$\mathrm{depends}... \\ $$$${y}\in\left[{a};\:{b}\right]\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:{a}\leqslant{y}\leqslant{b} \\ $$$$\Rightarrow\:{y}\in\mathbb{R}\backslash\left[{a};\:{b}\right]\:\mathrm{means}\:{y}<{a}\vee{y}>{b} \\ $$$$\left.{y}\in\right]{a};\:{b}\left[\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:{a}<{y}<{b}\right. \\ $$$$\left.\Rightarrow\:{y}\in\mathbb{R}\backslash\right]{a};\:{b}\left[\:\mathrm{means}\:{y}\leqslant{a}\vee{y}\geqslant{b}\right. \\ $$

Commented by jagoll last updated on 29/Jan/20

thanks you mister

$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{mister} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com