Question Number 79946 by mr W last updated on 29/Jan/20
![Find ∫_0 ^( n) [(x)^(1/3) ]dx=? in terms of n. (n∈N)](Q79946.png)
$${Find}\: \\ $$$$\int_{\mathrm{0}} ^{\:{n}} \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=?\: \\ $$$${in}\:{terms}\:{of}\:{n}.\:\left({n}\in\mathbb{N}\right) \\ $$
Answered by key of knowledge last updated on 29/Jan/20
![⌊^3 (√n)⌋=a ∫_m^3 ^( (m+1)^3 ) [^3 (√x^3 )]dx=m∫_m^3 ^((m+1)^3 ) dx=3m^3 +3m^2 +m ∫_0 ^( n) [(x)^(1/3) ]dx=Σ_0 ^(a−1) (3m^3 +3m^2 +m)+∫_a^3 ^( n) [(√x^3 )]= Σ_0 ^(a−1) (3m^3 +3m^2 +m)+a(n−a^3 )](Q79952.png)
$$\lfloor^{\mathrm{3}} \sqrt{\mathrm{n}}\rfloor=\mathrm{a} \\ $$$$\int_{\mathrm{m}^{\mathrm{3}} } ^{\:\left(\mathrm{m}+\mathrm{1}\right)^{\mathrm{3}} } \left[^{\mathrm{3}} \sqrt{\mathrm{x}^{\mathrm{3}} }\right]\mathrm{dx}=\mathrm{m}\int_{\mathrm{m}^{\mathrm{3}} } ^{\left(\mathrm{m}+\mathrm{1}\right)^{\mathrm{3}} } \mathrm{dx}=\mathrm{3m}^{\mathrm{3}} +\mathrm{3m}^{\mathrm{2}} +\mathrm{m} \\ $$$$\int_{\mathrm{0}} ^{\:{n}} \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=\underset{\mathrm{0}} {\overset{\mathrm{a}−\mathrm{1}} {\sum}}\left(\mathrm{3m}^{\mathrm{3}} +\mathrm{3m}^{\mathrm{2}} +\mathrm{m}\right)+\int_{\mathrm{a}^{\mathrm{3}} } ^{\:\mathrm{n}} \left[\sqrt{\mathrm{x}^{\mathrm{3}} }\right]=\: \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{a}−\mathrm{1}} {\sum}}\left(\mathrm{3m}^{\mathrm{3}} +\mathrm{3m}^{\mathrm{2}} +\mathrm{m}\right)+\mathrm{a}\left(\mathrm{n}−\mathrm{a}^{\mathrm{3}} \right) \\ $$$$ \\ $$
Commented by mr W last updated on 29/Jan/20
$${thanks}\:{alot}\:{sir}! \\ $$
Commented by mr W last updated on 29/Jan/20
$${i}\:{think}\:{you}\:{meant}\:\lfloor\sqrt[{\mathrm{3}}]{\mathrm{n}}\rfloor=\mathrm{a}\:{in}\:{the}\:{first} \\ $$$${line},\:{right}? \\ $$
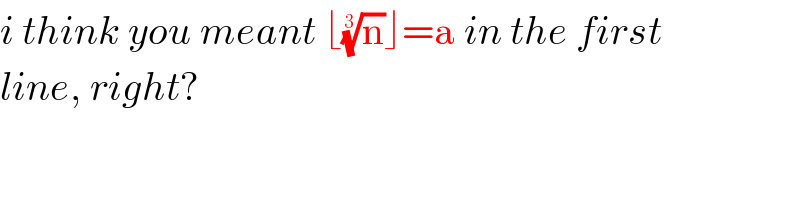
Commented by key of knowledge last updated on 29/Jan/20
$$\mathrm{yes}.\mathrm{Mr}\:\mathrm{W}\:.\mathrm{thank} \\ $$
Answered by mr W last updated on 29/Jan/20
![let h=⌊(n)^(1/3) ⌋ x=[0,1^3 ): [(x)^(1/3) ]=0 ⇒∫_0 ^1^3 [(x)^(1/3) ]dx=0×(1^3 −0) x=[1^3 ,2^3 ): [(x)^(1/3) ]=1⇒∫_0 ^1^3 [(x)^(1/3) ]dx=1×(2^3 −1^3 ) x=[2^3 ,3^3 ): [(x)^(1/3) ]=2⇒∫_1^3 ^2^3 [(x)^(1/3) ]dx=2×(3^3 −2^3 ) x=[3^3 ,4^3 ): [(x)^(1/3) ]=3⇒∫_2^3 ^3^3 [(x)^(1/3) ]dx=3×(4^3 −3^3 ) ... x=[(h−1)^3 ,h^3 ): [(x)^(1/3) ]=h−1⇒∫_((h−1)^3 ) ^h^3 [(x)^(1/3) ]dx=(h−1)×(h^3 −(h−1)^3 ) x=[h^3 ,n]: [(x)^(1/3) ]=h⇒∫_h^3 ^n [(x)^(1/3) ]dx=h×(n−h^3 ) ∫_0 ^( n) [(x)^(1/3) ]dx=Σ_(k=0) ^(h−1) ∫_k^3 ^((k+1)^3 ) [(x)^(1/3) ]dx+∫_h^3 ^n [(x)^(1/3) ]dx =Σ_(k=0) ^(h−1) {k[(k+1)^3 −k^3 ]}+h(n−h^3 ) =Σ_(k=1) ^(h−1) (3k^3 +3k^2 +k)+h(n−h^3 ) =3(((h−1)^2 h^2 )/4)+3(((h−1)h(2h−1))/6)+(((h−1)h)/2)+h(n−h^3 ) =((h^2 (h−1)(3h+1)+4h(n−h^3 ))/4) ⇒∫_0 ^( n) [(x)^(1/3) ]dx=nh−((h^2 (h+1)^2 )/4) example n=100: h=⌊((100))^(1/3) ⌋=4 ∫_0 ^( 100) [(x)^(1/3) ]dx=100×4−((4^2 ×5^2 )/4)=300](Q79962.png)
$${let}\:{h}=\lfloor\sqrt[{\mathrm{3}}]{{n}}\rfloor \\ $$$${x}=\left[\mathrm{0},\mathrm{1}^{\mathrm{3}} \right):\:\left[\sqrt[{\mathrm{3}}]{{x}}\right]=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}^{\mathrm{3}} } \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=\mathrm{0}×\left(\mathrm{1}^{\mathrm{3}} −\mathrm{0}\right) \\ $$$${x}=\left[\mathrm{1}^{\mathrm{3}} ,\mathrm{2}^{\mathrm{3}} \right):\:\left[\sqrt[{\mathrm{3}}]{{x}}\right]=\mathrm{1}\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}^{\mathrm{3}} } \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=\mathrm{1}×\left(\mathrm{2}^{\mathrm{3}} −\mathrm{1}^{\mathrm{3}} \right) \\ $$$${x}=\left[\mathrm{2}^{\mathrm{3}} ,\mathrm{3}^{\mathrm{3}} \right):\:\left[\sqrt[{\mathrm{3}}]{{x}}\right]=\mathrm{2}\Rightarrow\int_{\mathrm{1}^{\mathrm{3}} } ^{\mathrm{2}^{\mathrm{3}} } \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=\mathrm{2}×\left(\mathrm{3}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} \right) \\ $$$${x}=\left[\mathrm{3}^{\mathrm{3}} ,\mathrm{4}^{\mathrm{3}} \right):\:\left[\sqrt[{\mathrm{3}}]{{x}}\right]=\mathrm{3}\Rightarrow\int_{\mathrm{2}^{\mathrm{3}} } ^{\mathrm{3}^{\mathrm{3}} } \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=\mathrm{3}×\left(\mathrm{4}^{\mathrm{3}} −\mathrm{3}^{\mathrm{3}} \right) \\ $$$$... \\ $$$${x}=\left[\left({h}−\mathrm{1}\right)^{\mathrm{3}} ,{h}^{\mathrm{3}} \right):\:\left[\sqrt[{\mathrm{3}}]{{x}}\right]={h}−\mathrm{1}\Rightarrow\int_{\left({h}−\mathrm{1}\right)^{\mathrm{3}} } ^{{h}^{\mathrm{3}} } \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=\left({h}−\mathrm{1}\right)×\left({h}^{\mathrm{3}} −\left({h}−\mathrm{1}\right)^{\mathrm{3}} \right) \\ $$$${x}=\left[{h}^{\mathrm{3}} ,{n}\right]:\:\left[\sqrt[{\mathrm{3}}]{{x}}\right]={h}\Rightarrow\int_{{h}^{\mathrm{3}} } ^{{n}} \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}={h}×\left({n}−{h}^{\mathrm{3}} \right) \\ $$$$\int_{\mathrm{0}} ^{\:{n}} \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=\underset{{k}=\mathrm{0}} {\overset{{h}−\mathrm{1}} {\sum}}\int_{{k}^{\mathrm{3}} } ^{\left({k}+\mathrm{1}\right)^{\mathrm{3}} } \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}+\int_{{h}^{\mathrm{3}} } ^{{n}} \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{h}−\mathrm{1}} {\sum}}\left\{{k}\left[\left({k}+\mathrm{1}\right)^{\mathrm{3}} −{k}^{\mathrm{3}} \right]\right\}+{h}\left({n}−{h}^{\mathrm{3}} \right) \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{h}−\mathrm{1}} {\sum}}\left(\mathrm{3}{k}^{\mathrm{3}} +\mathrm{3}{k}^{\mathrm{2}} +{k}\right)+{h}\left({n}−{h}^{\mathrm{3}} \right) \\ $$$$=\mathrm{3}\frac{\left({h}−\mathrm{1}\right)^{\mathrm{2}} {h}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{3}\frac{\left({h}−\mathrm{1}\right){h}\left(\mathrm{2}{h}−\mathrm{1}\right)}{\mathrm{6}}+\frac{\left({h}−\mathrm{1}\right){h}}{\mathrm{2}}+{h}\left({n}−{h}^{\mathrm{3}} \right) \\ $$$$=\frac{{h}^{\mathrm{2}} \left({h}−\mathrm{1}\right)\left(\mathrm{3}{h}+\mathrm{1}\right)+\mathrm{4}{h}\left({n}−{h}^{\mathrm{3}} \right)}{\mathrm{4}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:{n}} \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}={nh}−\frac{{h}^{\mathrm{2}} \left({h}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$${example}\:{n}=\mathrm{100}: \\ $$$${h}=\lfloor\sqrt[{\mathrm{3}}]{\mathrm{100}}\rfloor=\mathrm{4} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{100}} \left[\sqrt[{\mathrm{3}}]{{x}}\right]{dx}=\mathrm{100}×\mathrm{4}−\frac{\mathrm{4}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{300} \\ $$