Σ_(n=1) ^∞ (1/((n+1)(n+2)(n+3)))=


Question and Answers Forum

All Questions Topic List
Arithmetic Questions
Previous in All Question Next in All Question
Previous in Arithmetic Next in Arithmetic
Question Number 80036 by jagoll last updated on 30/Jan/20

$\underset{n = 1}{\sum^{\infty}} \frac{1}{(n + 1) (n + 2) (n + 3)} =$
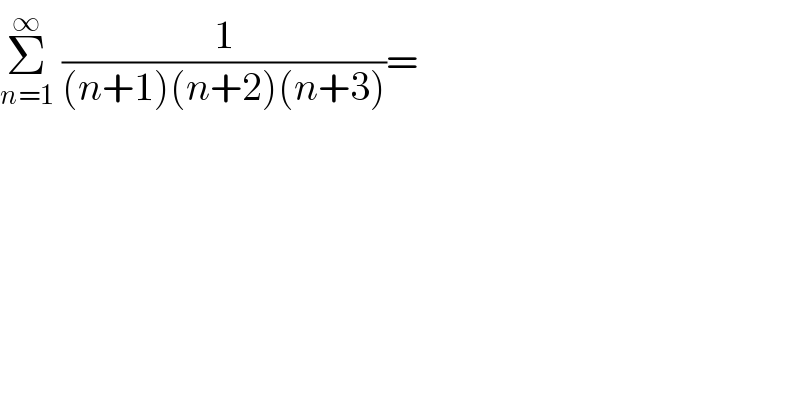
Commented by john santu last updated on 30/Jan/20
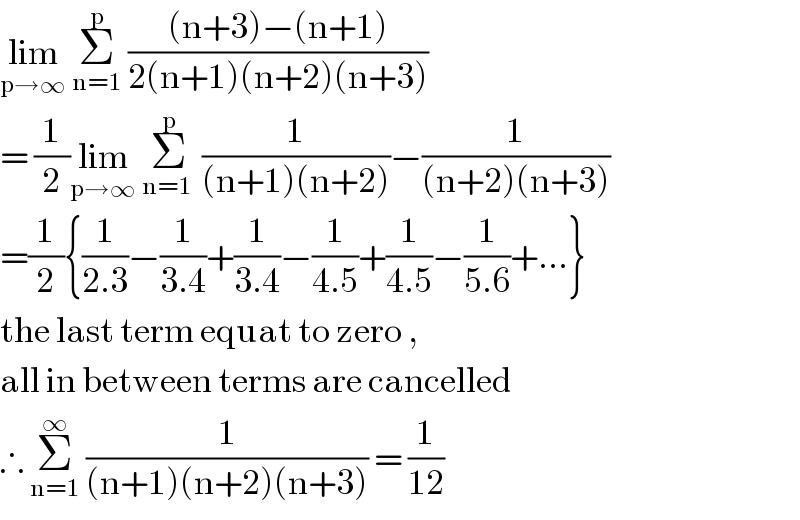
$lim_(p→∞) Σ_(n=1) ^p (((n+3)−(n+1))/(2(n+1)(n+2)(n+3))) = (1/2)lim_(p→∞) Σ_(n=1 ) ^p (1/((n+1)(n+2)))−(1/((n+2)(n+3))) =(1/2){(1/(2.3))−(1/(3.4))+(1/(3.4))−(1/(4.5))+(1/(4.5))−(1/(5.6))+...} the last term equat to zero , all in between terms are cancelled ∴ Σ_(n=1) ^∞ (1/((n+1)(n+2)(n+3))) = (1/(12))$
$\lim_{p \to \infty} \underset{n = 1}{\sum^{p}} \frac{(n + 3) - (n + 1)}{2 (n + 1) (n + 2) (n + 3)}$ $= \frac{1}{2} \lim_{p \to \infty} \underset{n = 1}{\sum^{p}} \frac{1}{(n + 1) (n + 2)} - \frac{1}{(n + 2) (n + 3)}$ $= \frac{1}{2} {\frac{1}{2.3} - \frac{1}{3.4} + \frac{1}{3.4} - \frac{1}{4.5} + \frac{1}{4.5} - \frac{1}{5.6} + . . .}$ $the last term equat to zero,$ $all in between terms are cancelled$ $∴ \underset{n = 1}{\sum^{\infty}} \frac{1}{(n + 1) (n + 2) (n + 3)} = \frac{1}{12}$
Commented by mr W last updated on 30/Jan/20

$t h e q u e s t i o n w a s o r i g i n a l l y$ $\underset{n = 1}{\sum^{\infty}} \frac{n}{(n + 1) (n + 2) (n + 3)} =$ $w h i c h h a s t h e r e s u l t \frac{1}{4} .$
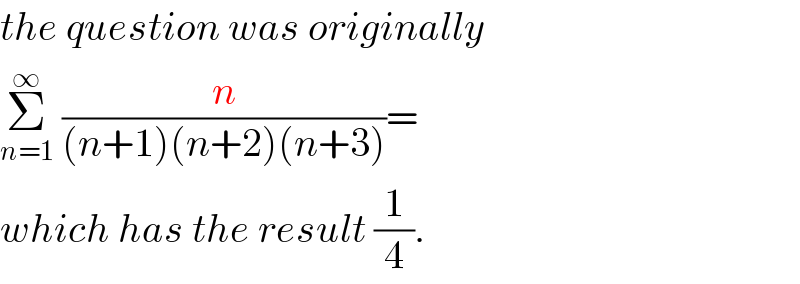
Commented by jagoll last updated on 31/Jan/20

$w a w . . . i h a v e t w o s o l u t i o n$ $(1) \underset{n = 1}{\sum^{\infty}} \frac{n}{(n + 1) (n + 2) (n + 3)} = \frac{1}{4}$ $(2) \underset{n = 1}{\sum^{\infty}} \frac{1}{(n + 1) (n + 2) (n + 3)} = \frac{1}{12}$ $t h a n k s y o u$
	Answered by Kamel Kamel last updated on 30/Jan/20

	$\frac{n}{(n + 1) (n + 2) (n + 3)} = \frac{A}{n + 1} + \frac{B}{n + 2} + \frac{C}{n + 3} . . . (E)$ $(E) \times (n + 1), n = - 1 \Rightarrow A = - \frac{1}{2}$ $(E) \times (n + 2), n = - 2 \Rightarrow B = 2$ $(E) \times (n + 3), n = - 3 \Rightarrow C = - \frac{3}{2}$ $∴ \frac{n}{(n + 1) (n + 2) (n + 3)} = \frac{1}{2} (\frac{1}{n + 2} - \frac{1}{n + 1}) - \frac{3}{2} (\frac{1}{n + 3} - \frac{1}{n + 2})$ $∴ \underset{n = 1}{\sum^{+ \infty}} \frac{n}{(n + 1) (n + 2) (n + 3)} = \frac{1}{2} (\underset{n = 1}{\sum^{+ \infty}} (\frac{1}{n + 2} - \frac{1}{n + 1}) - 3 \underset{n = 1}{\sum^{+ \infty}} (\frac{1}{n + 3} - \frac{1}{n + 2}))$ $= \frac{1}{2} ((\frac{1}{3} - \frac{1}{2} + \frac{1}{4} - \frac{1}{3} + . . .) - 3 (\frac{1}{4} - \frac{1}{3} + \frac{1}{5} - \frac{1}{4} + . . .))$ $= \frac{1}{2} (- \frac{1}{2} + 1) = \frac{1}{4}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum