Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 80039 by jagoll last updated on 30/Jan/20

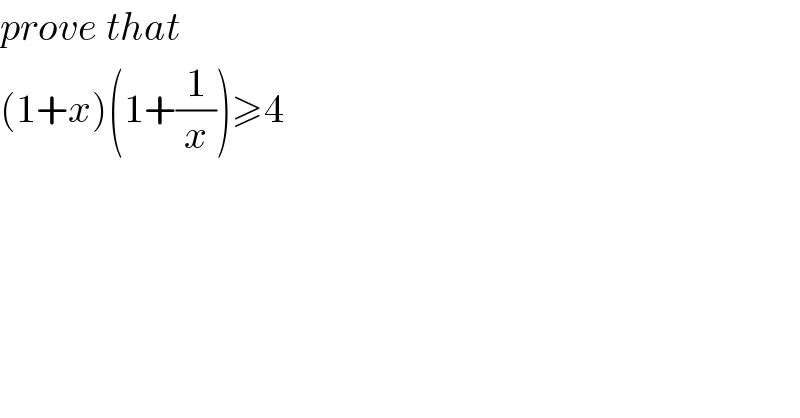
prove that (1+x)(1+(1/x))≥4

$${prove}\:{that} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\geqslant\mathrm{4} \\ $$

Commented by mr W last updated on 30/Jan/20

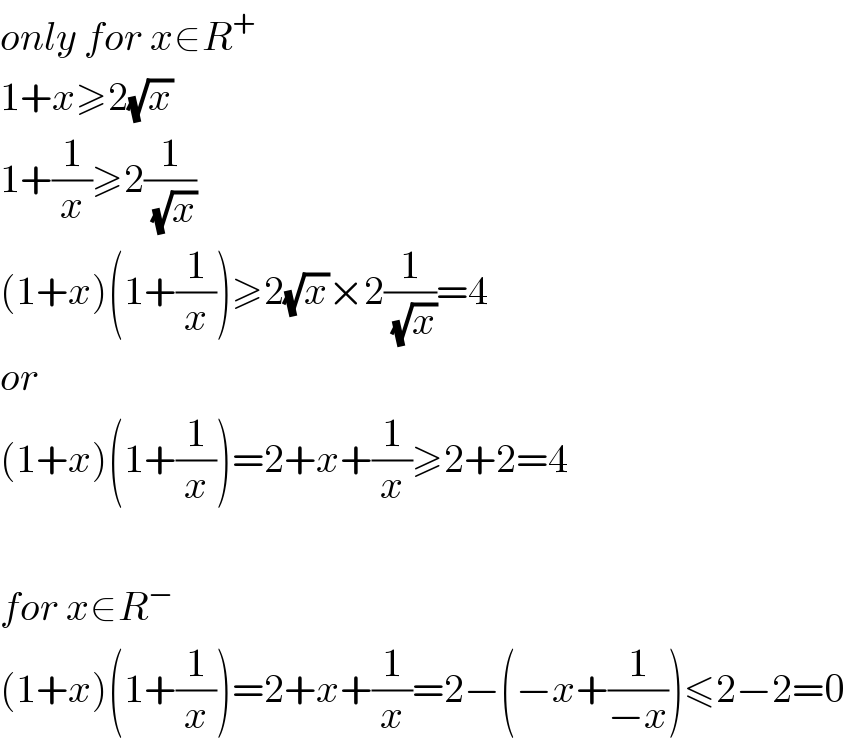
only for x∈R^+ 1+x≥2(√x) 1+(1/x)≥2(1/(√x)) (1+x)(1+(1/x))≥2(√x)×2(1/(√x))=4 or (1+x)(1+(1/x))=2+x+(1/x)≥2+2=4 for x∈R^− (1+x)(1+(1/x))=2+x+(1/x)=2−(−x+(1/(−x)))≤2−2=0

$${only}\:{for}\:{x}\in{R}^{+} \\ $$$$\mathrm{1}+{x}\geqslant\mathrm{2}\sqrt{{x}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{{x}}\geqslant\mathrm{2}\frac{\mathrm{1}}{\sqrt{{x}}} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\geqslant\mathrm{2}\sqrt{{x}}×\mathrm{2}\frac{\mathrm{1}}{\sqrt{{x}}}=\mathrm{4} \\ $$$${or} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{2}+{x}+\frac{\mathrm{1}}{{x}}\geqslant\mathrm{2}+\mathrm{2}=\mathrm{4} \\ $$$$ \\ $$$${for}\:{x}\in{R}^{−} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{2}+{x}+\frac{\mathrm{1}}{{x}}=\mathrm{2}−\left(−{x}+\frac{\mathrm{1}}{−{x}}\right)\leqslant\mathrm{2}−\mathrm{2}=\mathrm{0} \\ $$

Commented by Tony Lin last updated on 30/Jan/20

[1^2 +((√x))^2 ][1^2 +((1/(√x)))^2 ]≥(1+1)^2 =4

$$\left[\mathrm{1}^{\mathrm{2}} +\left(\sqrt{{x}}\right)^{\mathrm{2}} \right]\left[\mathrm{1}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\sqrt{{x}}}\right)^{\mathrm{2}} \right]\geqslant\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4} \\ $$

Commented by MJS last updated on 30/Jan/20

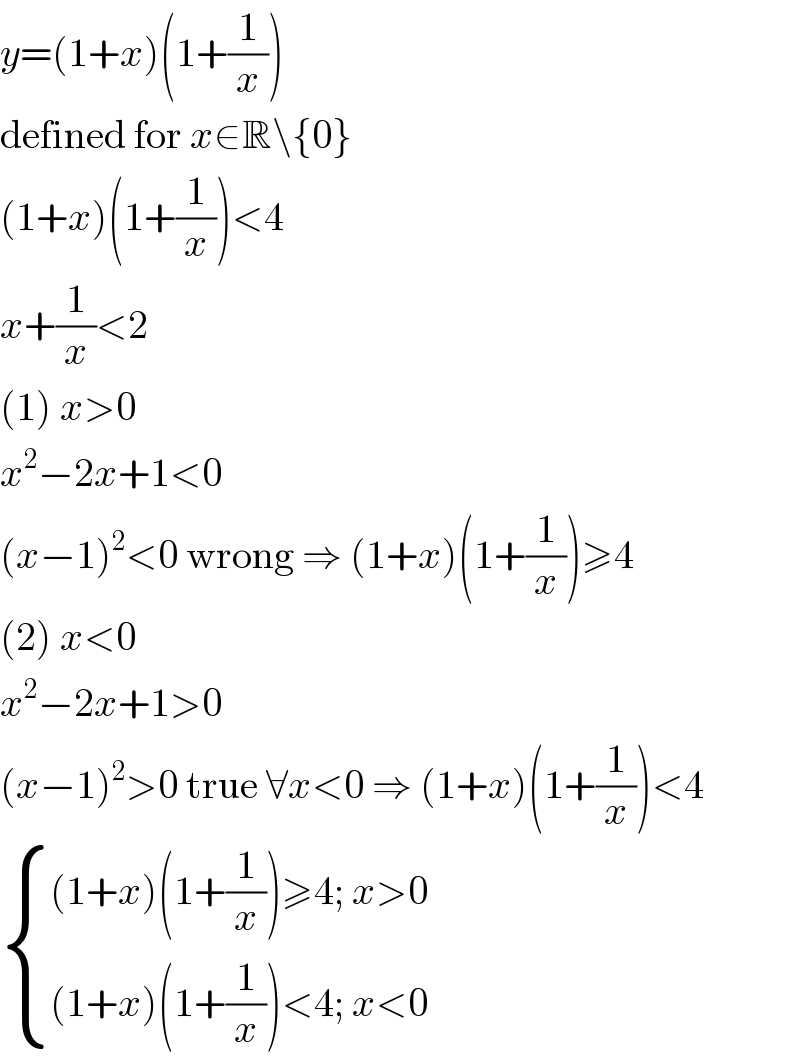
y=(1+x)(1+(1/x)) defined for x∈R\{0} (1+x)(1+(1/x))<4 x+(1/x)<2 (1) x>0 x^2 −2x+1<0 (x−1)^2 <0 wrong ⇒ (1+x)(1+(1/x))≥4 (2) x<0 x^2 −2x+1>0 (x−1)^2 >0 true ∀x<0 ⇒ (1+x)(1+(1/x))<4 { (((1+x)(1+(1/x))≥4; x>0)),(((1+x)(1+(1/x))<4; x<0)) :}

$${y}=\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right) \\ $$$$\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{R}\backslash\left\{\mathrm{0}\right\} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)<\mathrm{4} \\ $$$${x}+\frac{\mathrm{1}}{{x}}<\mathrm{2} \\ $$$$\left(\mathrm{1}\right)\:{x}>\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}<\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} <\mathrm{0}\:\mathrm{wrong}\:\Rightarrow\:\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\geqslant\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\:{x}<\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}>\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{0}\:\mathrm{true}\:\forall{x}<\mathrm{0}\:\Rightarrow\:\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)<\mathrm{4} \\ $$$$\begin{cases}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\geqslant\mathrm{4};\:{x}>\mathrm{0}}\\{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)<\mathrm{4};\:{x}<\mathrm{0}}\end{cases} \\ $$

Commented by mr W last updated on 30/Jan/20

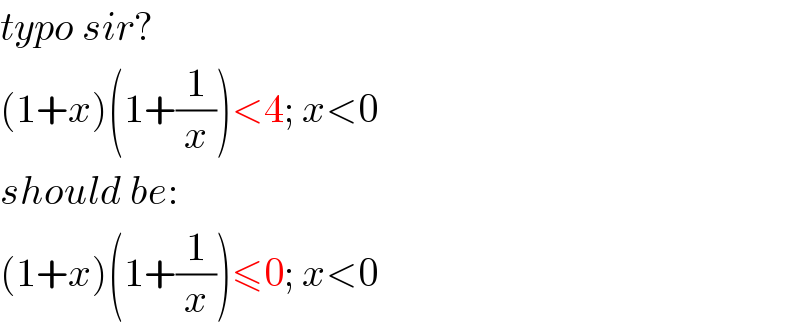
typo sir? (1+x)(1+(1/x))<4; x<0 should be: (1+x)(1+(1/x))≤0; x<0

$${typo}\:{sir}? \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)<\mathrm{4};\:{x}<\mathrm{0} \\ $$$${should}\:{be}: \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\leqslant\mathrm{0};\:{x}<\mathrm{0} \\ $$

Commented by MJS last updated on 30/Jan/20

You are right but with my method I only examined if it′s <4.

$$\mathrm{You}\:\mathrm{are}\:\mathrm{right}\:\mathrm{but}\:\mathrm{with}\:\mathrm{my}\:\mathrm{method}\:\mathrm{I}\:\mathrm{only} \\ $$$$\mathrm{examined}\:\mathrm{if}\:\mathrm{it}'\mathrm{s}\:<\mathrm{4}. \\ $$

Commented by jagoll last updated on 31/Jan/20

thank you

$${thank}\:{you}\: \\ $$

Answered by $@ty@m123 last updated on 31/Jan/20

Let y=(1+x)(1+(1/x)) ⇒y=2+x+(1/x) (dy/dx)=1−(1/x^2 ) For max. or min. (dy/dx)=0 1−(1/x^2 )=0 ⇒x=±1 y∣_(x=1) =4, y∣_(x=−1) =0 (d^2 y/dx^2 )=(1/x^3 ) [(d^2 y/dx^2 )]_(x=1) =1>0 ∴ y is mininmum at x=1 and min.(y)=4

$${Let}\:{y}=\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right) \\ $$$$\Rightarrow{y}=\mathrm{2}+{x}+\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${For}\:{max}.\:{or}\:{min}. \\ $$$$\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{x}=\pm\mathrm{1} \\ $$$${y}\mid_{{x}=\mathrm{1}} \:=\mathrm{4}, \\ $$$${y}\mid_{{x}=−\mathrm{1}} =\mathrm{0} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\mathrm{1}}{{x}^{\mathrm{3}} } \\ $$$$\left[\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right]_{{x}=\mathrm{1}} =\mathrm{1}>\mathrm{0} \\ $$$$\therefore\:{y}\:{is}\:{mininmum}\:{at}\:{x}=\mathrm{1} \\ $$$${and}\:{min}.\left({y}\right)=\mathrm{4} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com