Question Number 80064 by Rio Michael last updated on 30/Jan/20
![lim_(x→−∞) [(√(1−xe^x ))]](Q80064.png)
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\left[\sqrt{\mathrm{1}−{xe}^{{x}} \:}\right] \\ $$
Commented by mathmax by abdo last updated on 30/Jan/20
$${no}\:{its}\:{a}\:{indeterminedform}\:\:{its}\:{not}\:{correct} \\ $$
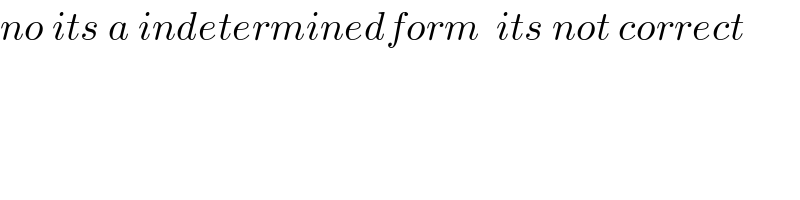
Commented by mr W last updated on 30/Jan/20
![let t=−x t→+∞ when x→−∞ lim_(x→−∞) (1−xe^x )=lim_(t→+∞) (1+(t/e^t )) =1+lim_(t→+∞) ((t/e^t )) =1+lim_(t→+∞) ((1/e^t )) =1+0 =1 ⇒lim_(x→−∞) [(√(1−xe^x ))]=(√1)=1](Q80079.png)
$${let}\:{t}=−{x} \\ $$$${t}\rightarrow+\infty\:{when}\:{x}\rightarrow−\infty \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(\mathrm{1}−{xe}^{{x}} \right)=\underset{{t}\rightarrow+\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{{t}}{{e}^{{t}} }\right) \\ $$$$=\mathrm{1}+\underset{{t}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{{t}}{{e}^{{t}} }\right) \\ $$$$=\mathrm{1}+\underset{{t}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{e}^{{t}} }\right) \\ $$$$=\mathrm{1}+\mathrm{0} \\ $$$$=\mathrm{1} \\ $$$$\Rightarrow\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\left[\sqrt{\mathrm{1}−{xe}^{{x}} \:}\right]=\sqrt{\mathrm{1}}=\mathrm{1} \\ $$
Commented by Rio Michael last updated on 30/Jan/20
$${thanks}\:{sir} \\ $$
Commented by Rio Michael last updated on 30/Jan/20
![sir i solved it like this: lim_(x→−∞) [(√(1−xe^x ))] = (√(1−(−∞)e^(−∞) )) = (√( 1+ ((+∞)/e^∞ ) )) = (√(1+0)) = 1](Q80082.png)
$$\mathrm{sir}\:\mathrm{i}\:\mathrm{solved}\:\mathrm{it}\:\mathrm{like}\:\mathrm{this}: \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\left[\sqrt{\mathrm{1}−{xe}^{{x}} }\right]\:=\:\sqrt{\mathrm{1}−\left(−\infty\right){e}^{−\infty} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\:\mathrm{1}+\:\frac{+\infty}{{e}^{\infty} }\:}\:=\:\sqrt{\mathrm{1}+\mathrm{0}}\:=\:\mathrm{1} \\ $$$$ \\ $$
Commented by Rio Michael last updated on 30/Jan/20
$${you}\:{mean}\:{i}\:{must}\:{do}\:{the}\:{substitution}\:{t}\:=\:−{x}? \\ $$
Commented by mathmax by abdo last updated on 04/Feb/20
$${let}\:{f}\left({x}\right)=\sqrt{\mathrm{1}−{xe}^{{x}} }\:\:{cha}\mathrm{7}{gement}\:\:{e}^{{x}} ={t}\:{give}\:{x}={ln}\left({t}\right) \\ $$$$\Rightarrow{lim}_{{x}\rightarrow−\infty} {f}\left({x}\right)={lim}_{{t}\rightarrow\mathrm{0}^{+} } \:\:\sqrt{\mathrm{1}−{tlnt}}=\sqrt{\mathrm{1}−{o}}=\mathrm{1} \\ $$
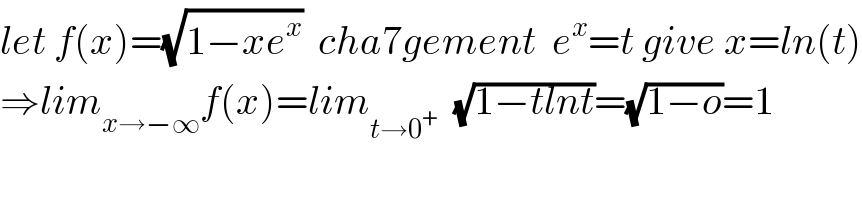
Answered by Kamel Kamel last updated on 30/Jan/20
![We have: ∀x⋘0, 0<−xe^x <1 So :(√(1−xe^x ))=1+α /α<1 ∴ [(√(1−xe^x ))]=1 ∴ lim_(x→−∞) [(√(1−xe^x ))]=1](Q80083.png)
$$\mathrm{We}\:\mathrm{have}:\:\forall\mathrm{x}\lll\mathrm{0},\:\mathrm{0}<−\mathrm{xe}^{\mathrm{x}} <\mathrm{1} \\ $$$$\mathrm{So}\::\sqrt{\mathrm{1}−\mathrm{xe}^{\mathrm{x}} }=\mathrm{1}+\alpha\:/\alpha<\mathrm{1} \\ $$$$\therefore\:\left[\sqrt{\mathrm{1}−\mathrm{xe}^{\mathrm{x}} }\right]=\mathrm{1} \\ $$$$\therefore\:\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\left[\sqrt{\mathrm{1}−{xe}^{{x}} \:}\right]=\mathrm{1} \\ $$