Question Number 80084 by behi83417@gmail.com last updated on 30/Jan/20
$$\:\:−\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{1}} =\left(−\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{2}}} =\left(\left(−\mathrm{1}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\left(\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} = \\ $$$$=\sqrt{\mathrm{1}}=\mathrm{1}\:\: \\ $$$$\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{think}\:\mathrm{about}\:\mathrm{this}? \\ $$
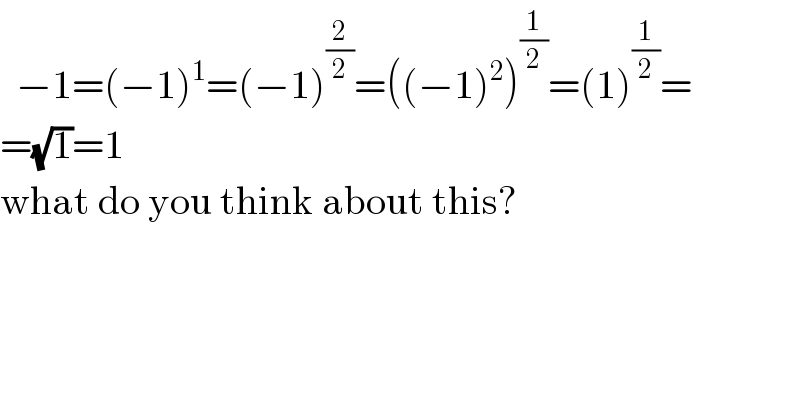
Commented by key of knowledge last updated on 30/Jan/20
$$\left(−\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{2}}} =\left(\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\mathrm{2}} \neq\left(\left(−\mathrm{1}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$
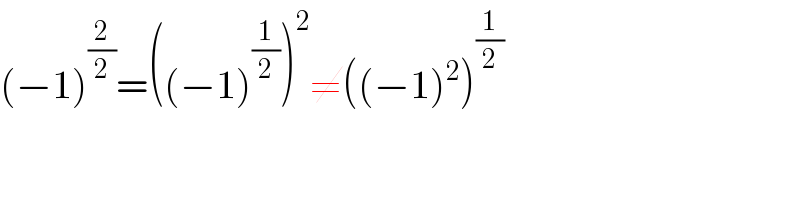
Commented by behi83417@gmail.com last updated on 31/Jan/20
$$\mathrm{thanks}\:\mathrm{alot}\:\mathrm{sir}'\mathrm{s}. \\ $$$$\mathrm{perfect}\:\mathrm{explanation}. \\ $$
Commented by MJS last updated on 31/Jan/20
![we′ve got a definition: C={z=e^(iθ) r∣−π<θ≤π; r∈R^+ } we know that e^(iθ) =e^(i(θ+2πn)) with n∈Z but we only use this for finding all possible solutions of certain equations we define z^q =(e^(iθ) r)^q =e^(i(π−mod (π−qθ, 2π)) r^q for q∈Q, R, C with mod (x, y) ≥0 i.e. mod (−3, 7)=4 [there′s only one exception for z∈R^+ and n∈Z: (−z)^(1/(2n+1)) =−(z^(1/(2n+1)) ) This is useful in elementary mathematics, like 3d geometry or solving polynomes of 3^(rd) degree using Cardano.] ⇒ (z^q )^(1/q) ≠(z^(1/q) )^q in many cases ((−1)^2 )^(1/2) =(1)^(1/2) =1 ((−1)^(1/2) )^2 =(i)^2 =−1 ((3+4i)^4 )^(1/4) =4−3i ((3+4i)^(1/4) )^4 =3+4i](Q80106.png)
$$\mathrm{we}'\mathrm{ve}\:\mathrm{got}\:\mathrm{a}\:\mathrm{definition}: \\ $$$$\mathbb{C}=\left\{{z}=\mathrm{e}^{\mathrm{i}\theta} {r}\mid−\pi<\theta\leqslant\pi;\:{r}\in\mathbb{R}^{+} \right\} \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{e}^{\mathrm{i}\theta} =\mathrm{e}^{\mathrm{i}\left(\theta+\mathrm{2}\pi{n}\right)} \:\mathrm{with}\:{n}\in\mathbb{Z}\:\mathrm{but}\:\mathrm{we} \\ $$$$\mathrm{only}\:\mathrm{use}\:\mathrm{this}\:\mathrm{for}\:\mathrm{finding}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{solutions} \\ $$$$\mathrm{of}\:\mathrm{certain}\:\mathrm{equations} \\ $$$$\mathrm{we}\:\mathrm{define} \\ $$$${z}^{{q}} =\left(\mathrm{e}^{\mathrm{i}\theta} {r}\right)^{{q}} =\mathrm{e}^{\mathrm{i}\left(\pi−\mathrm{mod}\:\left(\pi−{q}\theta,\:\mathrm{2}\pi\right)\right.} {r}^{{q}} \:\mathrm{for}\:{q}\in\mathbb{Q},\:\mathbb{R},\:\mathbb{C} \\ $$$$\mathrm{with}\:\mathrm{mod}\:\left({x},\:{y}\right)\:\geqslant\mathrm{0}\:\mathrm{i}.\mathrm{e}.\:\mathrm{mod}\:\left(−\mathrm{3},\:\mathrm{7}\right)=\mathrm{4} \\ $$$$\:\:\:\:\:\left[\mathrm{there}'\mathrm{s}\:\mathrm{only}\:\mathrm{one}\:\mathrm{exception}\:\mathrm{for}\:{z}\in\mathbb{R}^{+} \:\mathrm{and}\right. \\ $$$$\:\:\:\:\:\:\:{n}\in\mathbb{Z}:\:\left(−{z}\right)^{\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}} =−\left({z}^{\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}} \right)\:\mathrm{This}\:\mathrm{is}\:\mathrm{useful}\:\mathrm{in} \\ $$$$\:\:\:\:\:\:\:\mathrm{elementary}\:\mathrm{mathematics},\:\mathrm{like}\:\mathrm{3d}\:\mathrm{geometry} \\ $$$$\:\:\:\:\:\:\:\mathrm{or}\:\mathrm{solving}\:\mathrm{polynomes}\:\mathrm{of}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{using} \\ $$$$\left.\:\:\:\:\:\:\:\mathrm{Cardano}.\right] \\ $$$$\Rightarrow\:\left({z}^{{q}} \right)^{\frac{\mathrm{1}}{{q}}} \neq\left({z}^{\frac{\mathrm{1}}{{q}}} \right)^{{q}} \:\mathrm{in}\:\mathrm{many}\:\mathrm{cases} \\ $$$$\left(\left(−\mathrm{1}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\left(\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1} \\ $$$$\left(\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\mathrm{2}} =\left(\mathrm{i}\right)^{\mathrm{2}} =−\mathrm{1} \\ $$$$\left(\left(\mathrm{3}+\mathrm{4i}\right)^{\mathrm{4}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} =\mathrm{4}−\mathrm{3i} \\ $$$$\left(\left(\mathrm{3}+\mathrm{4i}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \right)^{\mathrm{4}} =\mathrm{3}+\mathrm{4i} \\ $$