
Question and Answers Forum
Question Number 80175 by Rio Michael last updated on 31/Jan/20
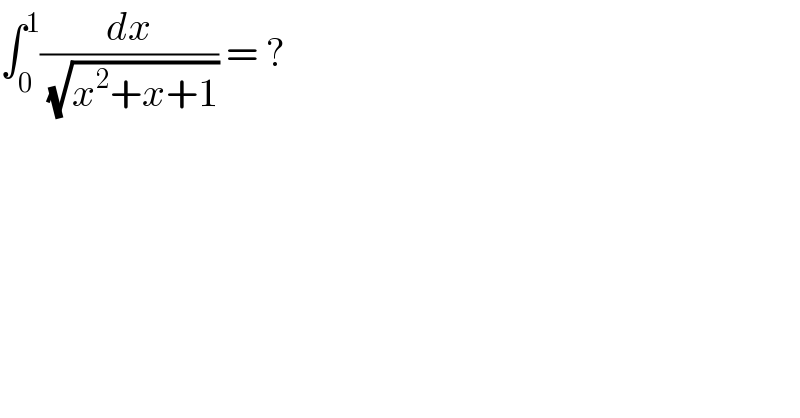
Commented by mathmax by abdo last updated on 31/Jan/20
![let I=∫_0 ^1 (dx/(√(x^2 +x+1))) ⇒I=∫_0 ^1 (dx/(√((x+(1/2))^2 +(3/4)))) cha7gement x+(1/2) =((√3)/2)tanθ give θ =arctan(((2x+1)/(√3))) I=∫_(π/6) ^(π/3) (1/((√(3/4))(√(1+tan^2 θ))))×((√3)/2) (1+tan^2 θ)dθ =∫_(π/6) ^(π/3) (√(1+tan^2 θ))dθ =∫_(π/6) ^(π/3) (dθ/(cosθ)) =_(tan((θ/2))=u) ∫_(2−(√3)) ^(1/(√3)) (1/((1−u^2 )/(1+u^2 )))×((2du)/(1+u^2 )) =∫_(2−(√3)) ^(1/(√3)) ((1/(1−u))+(1/(1+u)))du =[ln∣((1+u)/(1−u))∣]_(2−(√3)) ^(1/(√3)) =ln∣((1+(1/(√3)))/(1−(1/(√3))))∣−ln∣((3−(√3))/(−1+(√3)))∣=ln∣(√3)+1∣−ln∣(√3)−1∣−ln∣(((√3)((√3)−1))/((√3)−1))∣ =ln((√3)+1)−ln((√3)−1)−ln((√3))](Q80194.png)
Answered by ~blr237~ last updated on 31/Jan/20
![Let named it A using 1+x+x^2 =(x+(1/2))^2 +(3/4) = (3/4)[(((2x+1)/(√3)))^2 +1] A=∫_0 ^1 (2/(√3)) (1/(√([(((2x+1)/(√3)))^2 +1))) dx =[argsh(((2x+1)/(√3)))]_0 ^1 = argsh((√3) )−argsh((1/(√3))) using argshx=ln(x+(√(1+x^2 )) ) A=ln(2+(√3))−ln((√3) )](Q80177.png)
| ||
Question and Answers Forum | ||
Question Number 80175 by Rio Michael last updated on 31/Jan/20 | ||
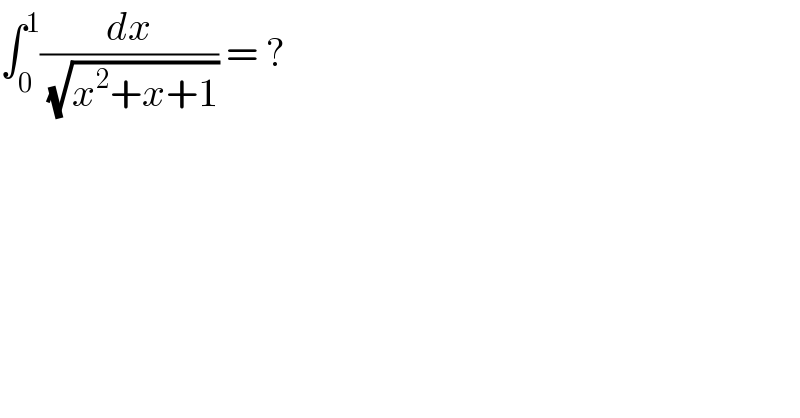 | ||
Commented by mathmax by abdo last updated on 31/Jan/20 | ||
![let I=∫_0 ^1 (dx/(√(x^2 +x+1))) ⇒I=∫_0 ^1 (dx/(√((x+(1/2))^2 +(3/4)))) cha7gement x+(1/2) =((√3)/2)tanθ give θ =arctan(((2x+1)/(√3))) I=∫_(π/6) ^(π/3) (1/((√(3/4))(√(1+tan^2 θ))))×((√3)/2) (1+tan^2 θ)dθ =∫_(π/6) ^(π/3) (√(1+tan^2 θ))dθ =∫_(π/6) ^(π/3) (dθ/(cosθ)) =_(tan((θ/2))=u) ∫_(2−(√3)) ^(1/(√3)) (1/((1−u^2 )/(1+u^2 )))×((2du)/(1+u^2 )) =∫_(2−(√3)) ^(1/(√3)) ((1/(1−u))+(1/(1+u)))du =[ln∣((1+u)/(1−u))∣]_(2−(√3)) ^(1/(√3)) =ln∣((1+(1/(√3)))/(1−(1/(√3))))∣−ln∣((3−(√3))/(−1+(√3)))∣=ln∣(√3)+1∣−ln∣(√3)−1∣−ln∣(((√3)((√3)−1))/((√3)−1))∣ =ln((√3)+1)−ln((√3)−1)−ln((√3))](Q80194.png) | ||
Answered by ~blr237~ last updated on 31/Jan/20 | ||
![Let named it A using 1+x+x^2 =(x+(1/2))^2 +(3/4) = (3/4)[(((2x+1)/(√3)))^2 +1] A=∫_0 ^1 (2/(√3)) (1/(√([(((2x+1)/(√3)))^2 +1))) dx =[argsh(((2x+1)/(√3)))]_0 ^1 = argsh((√3) )−argsh((1/(√3))) using argshx=ln(x+(√(1+x^2 )) ) A=ln(2+(√3))−ln((√3) )](Q80177.png) | ||
| ||