Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 80180 by mathocean1 last updated on 31/Jan/20

$$\mathrm{h}\left(x\right)=\frac{x-x^2}{x+1}$$$$wedefinedthisfunctionon$$$$\mathbb{R}-\{-1\}\to \mathbb{R}$$$$$$$$1)\mathrm{Study}\mathrm{the}\mathrm{variations}\mathrm{of}\mathrm{h}\mathrm{then}$$$$\mathrm{draw}\mathrm{up}\mathrm{its}\mathrm{table}\mathrm{of}\mathrm{variation}.$$$$$$$$\mathrm{please}\mathrm{sirs}\mathrm{i}\mathrm{need}\mathrm{your}\mathrm{kind}\mathrm{help}$$

Answered by Rio Michael last updated on 31/Jan/20

$$\mathbf{solution}$$$$----------$$$$\mathrm{h}\left(x\right)=\frac{x-x^2}{x-1}$$$$h\left(x\right)=0\Rightarrow x-x^2=0\Rightarrow x=0orx=1$$$${\mathrm{h}}^{\prime }\left(x\right)=\frac{(x-x^2)-(x-1)(1-2x)}{{(x-1)}^2}=\frac{x-x^2-(x-2x^2-1+2x)}{{(x-1)}^2}$$$$h^{{}^{\prime }}\left(x\right)=\frac{x^2-2x+1}{{(x-1)}^2}$$$$h^{{}^{\prime }}\left(x\right)>0\Rightarrow {(x-1)}^2>0\Rightarrow x>1$$$$hisincreasingforx>1anddecreasingotherwise$$$$$$

Commented by mathocean1 last updated on 31/Jan/20

$$\mathrm{Please}\mathrm{sir}{\mathrm{h}}^{\prime }\mathrm{is}\mathrm{not}\mathrm{like}\mathrm{this}:$$$${\mathrm{h}}^{\prime }=\frac{(1-2x)(x+1)-(x-x^2)}{{(x+1)}^2}?$$$$$$

Commented by mathocean1 last updated on 31/Jan/20

$$\mathrm{h}\left(x\right)=\frac{x-x^2}{x+1}$$

Commented by Rio Michael last updated on 31/Jan/20

$$sorryicopiedthequestionwrongly$$

Commented by mathocean1 last updated on 31/Jan/20

$$\mathrm{please}\mathrm{sir}\mathrm{how}\mathrm{can}\mathrm{i}\mathrm{draw}\mathrm{up}\mathrm{its}$$$$\mathrm{table}\mathrm{of}\mathrm{variation}\mathrm{when}$$$${\mathrm{h}}^{\prime }=\frac{-x^2-2x+1}{{(x+1)}^2}=-1?$$

Commented by JDamian last updated on 01/Feb/20

$$if\mathrm{h}\left(x\right)were\frac{x-x^2}{x-1},then\mathrm{h}\left(x\right)=\frac{x(1-x)}{x-1}=-x$$$$averyeasyfunction$$

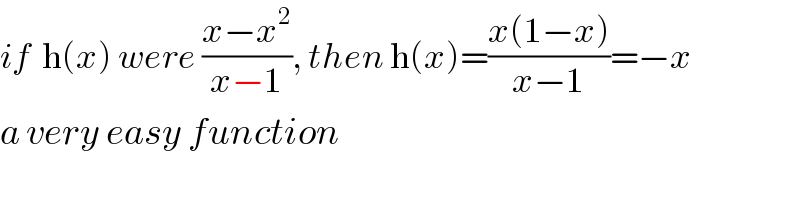
Commented by mathocean1 last updated on 01/Feb/20

$$\mathrm{so}...\mathrm{we}\mathrm{can}\mathrm{study}\mathrm{h}\left(x\right)=\frac{x-x^2}{x+1}???$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com