Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 80209 by peter frank last updated on 01/Feb/20

Commented by mathmax by abdo last updated on 01/Feb/20

$z + \frac{1}{z} = - 1 \Rightarrow z^{2} + 1 = - z \Rightarrow z^{2} + z + 1 = 0$ $Δ = 1 - 4 = - 3 \Rightarrow z_{1} = \frac{- 1 + i \sqrt{3}}{2} = e^{\frac{i 2 π}{3}} a n d z_{2} = \frac{- 1 - i \sqrt{3}}{2} = e^{- \frac{i 2 π}{3}}$ $z = z_{1} \Rightarrow z^{5} + \frac{1}{z^{5}} = e^{\frac{i 10 π}{3}} + e^{- \frac{i 10 π}{3}} = 2 c o s (\frac{10 π}{3}) = 2 c o s (4 π - \frac{2 π}{3})$ $= 2 c o s (\frac{2 π}{3}) = 2 \times (- \frac{1}{2}) = - 1$ $z = z_{2} w e g e t t h e s a m e v a l u e b e c a u s e z_{2} = c o n j (z_{1})$ $f o r z^{11} + \frac{1}{z^{11}}$ $z = z_{1} =\Rightarrow z^{11} + \frac{1}{z^{11}} = e^{\frac{i 22 π}{3}} + e^{- \frac{i 22 π}{3}} = 2 c o s (\frac{22 π}{3})$ $= 2 c o s (8 π - \frac{2 π}{3}) = 2 c o s (\frac{2 π}{3}) = - 1$ $z = z_{2} w e g e t t h e s a m e v a l u e$
	Answered by som(math1967) last updated on 01/Feb/20

	${(z + \frac{1}{z})}^{2} = 1 \Rightarrow z^{2} + \frac{1}{z^{2}} = 1 - 2 = - 1$ $a g a i n {(z + \frac{1}{z})}^{3} = - 1$ $z^{3} + \frac{1}{z^{3}} + 3 (z + \frac{1}{z}) = - 1$ $z^{3} + \frac{1}{z^{3}} = - 1 + 3 = 2$ $∴ (z^{2} + \frac{1}{z^{2}}) (z^{3} + \frac{1}{z^{3}}) = (- 1) (2) = - 2$ $z^{5} + \frac{1}{z^{5}} + z + \frac{1}{z} = - 2$ $∴ z^{5} + \frac{1}{z^{5}} = - 2 + 1 = - 1 (p r o v e d)$ $A g a i n {(z^{3} + \frac{1}{z^{3}})}^{2} = 4$ $z^{6} + \frac{1}{z^{6}} = 4 - 2 = 2$ $∴ (z^{5} + \frac{1}{z^{5}}) (z^{6} + \frac{1}{z^{6}}) = (- 1) (2)$ $z^{11} + \frac{1}{z^{11}} + z + \frac{1}{z} = - 2$ $∴ z^{11} + \frac{1}{z^{11}} = - 2 + 1 = - 1 a n s$
	Answered by mr W last updated on 01/Feb/20
	$z+(1/z)=−1 z^2 +z+1=0 z=((−1±i(√3))/2)=−{cos (±(π/3))+sin (±(π/3)) i}=−e^(±(π/3)i) z^n +(1/z^n )=(−1)^n [e^(±((nπ)/3)i) +e^(∓((nπ)/3)i) ] =2(−1)^n cos (±((nπ)/3)) =2(−1)^n cos (((nπ)/3)) ⇒z^n +(1/z^n )=2(−1)^n cos (((nπ)/3)) n=5: z^5 +(1/z^5 )=2(−1)^5 cos (((5π)/3))=−2×(1/2)=−1 n=11: z^(11) +(1/z^(11) )=2(−1)^(11) cos (((11π)/3))=−2×(1/2)=−1 n=3: z^3 +(1/z^3 )=2(−1)^3 cos (((3π)/3))=−2×(−1)=2 n=12: z^(12) +(1/z^(12) )=2(−1)^(12) cos (((12π)/3))=2×1=2$
	$z + \frac{1}{z} = - 1$ $z^{2} + z + 1 = 0$ $z = \frac{- 1 \pm i \sqrt{3}}{2} = - {\cos (\pm \frac{π}{3}) + \sin (\pm \frac{π}{3}) i} = - e^{\pm \frac{π}{3} i}$ $z^{n} + \frac{1}{z^{n}} = {(- 1)}^{n} [e^{\pm \frac{n π}{3} i} + e^{\mp \frac{n π}{3} i}]$ $= 2 {(- 1)}^{n} \cos (\pm \frac{n π}{3})$ $= 2 {(- 1)}^{n} \cos (\frac{n π}{3})$ $\Rightarrow z^{n} + \frac{1}{z^{n}} = 2 {(- 1)}^{n} \cos (\frac{n π}{3})$ $n = 5 :$ $z^{5} + \frac{1}{z^{5}} = 2 {(- 1)}^{5} \cos (\frac{5 π}{3}) = - 2 \times \frac{1}{2} = - 1$ $n = 11 :$ $z^{11} + \frac{1}{z^{11}} = 2 {(- 1)}^{11} \cos (\frac{11 π}{3}) = - 2 \times \frac{1}{2} = - 1$ $n = 3 :$ $z^{3} + \frac{1}{z^{3}} = 2 {(- 1)}^{3} \cos (\frac{3 π}{3}) = - 2 \times (- 1) = 2$ $n = 12 :$ $z^{12} + \frac{1}{z^{12}} = 2 {(- 1)}^{12} \cos (\frac{12 π}{3}) = 2 \times 1 = 2$
	Commented by jagoll last updated on 01/Feb/20

	$i f x + \frac{1}{x} = - 2$ $t h a t x^{6} + \frac{1}{x^{6}} = 2 {(- 2)}^{6} \times \cos (\frac{6 π}{3})$ $= 128 . t h a t r i g h t s i r$
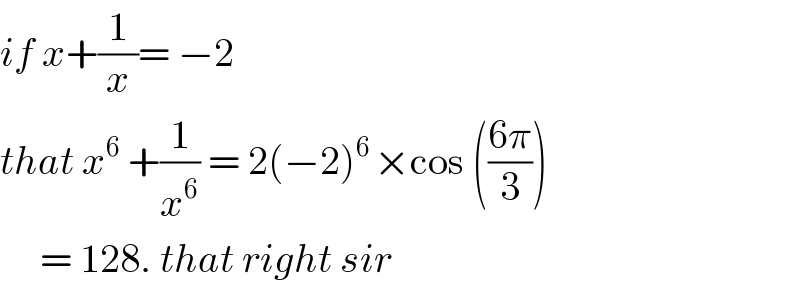
	Commented by mr W last updated on 01/Feb/20

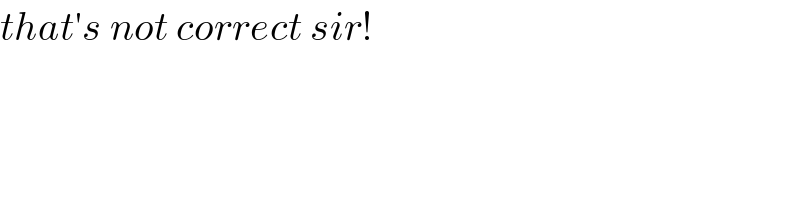
	${t h a t}^{'} s n o t c o r r e c t s i r!$
	Commented by peter frank last updated on 01/Feb/20

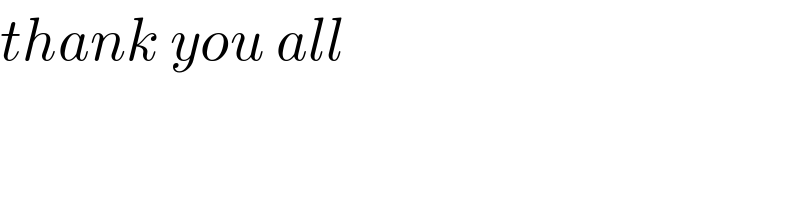
	$t h a n k y o u a l l$
	Commented by mr W last updated on 01/Feb/20

	$i f x + \frac{1}{x} = - 2$ $\Rightarrow x = - 1$ $\Rightarrow x^{3} + \frac{1}{x^{3}} = - 2$ $\Rightarrow x^{6} + \frac{1}{x^{6}} = 2$
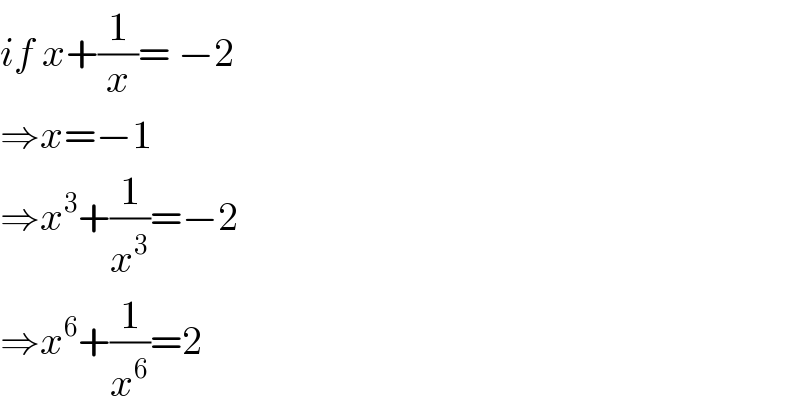
	Commented by jagoll last updated on 01/Feb/20

	$s p e c i a l m e a n s o n l y f o r f o r m$ $x + \frac{1}{x} = - 1$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum