Question and Answers Forum
Question Number 80222 by mr W last updated on 01/Feb/20
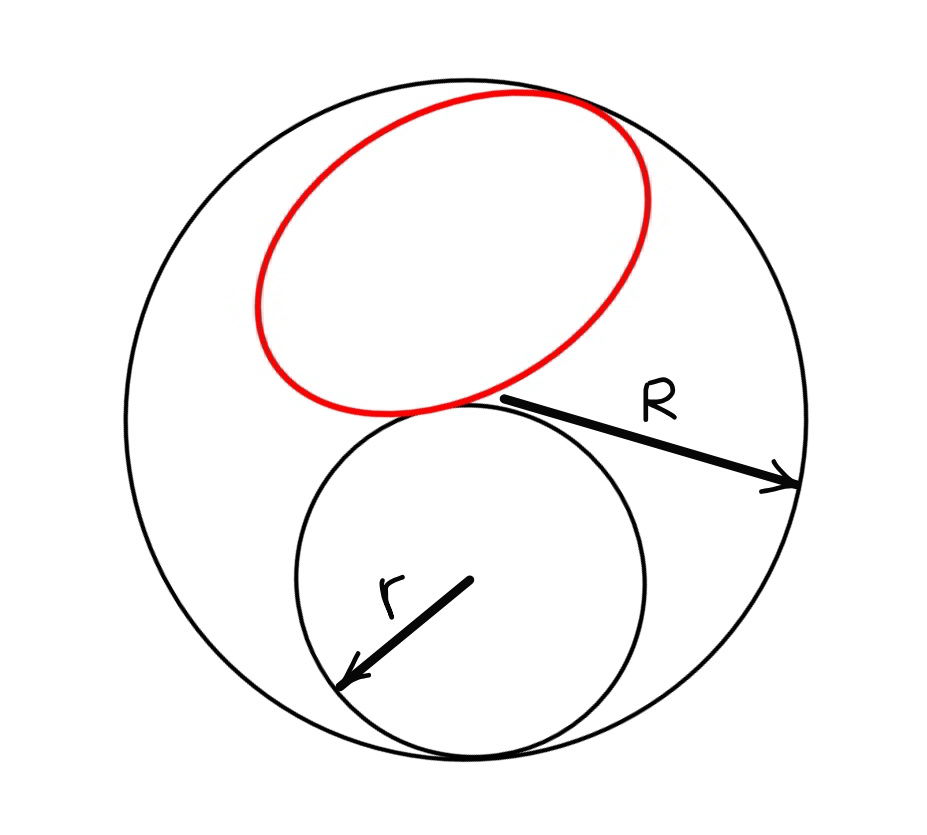
Commented by mr W last updated on 01/Feb/20

Commented by behi83417@gmail.com last updated on 01/Feb/20

Answered by mr W last updated on 02/Feb/20
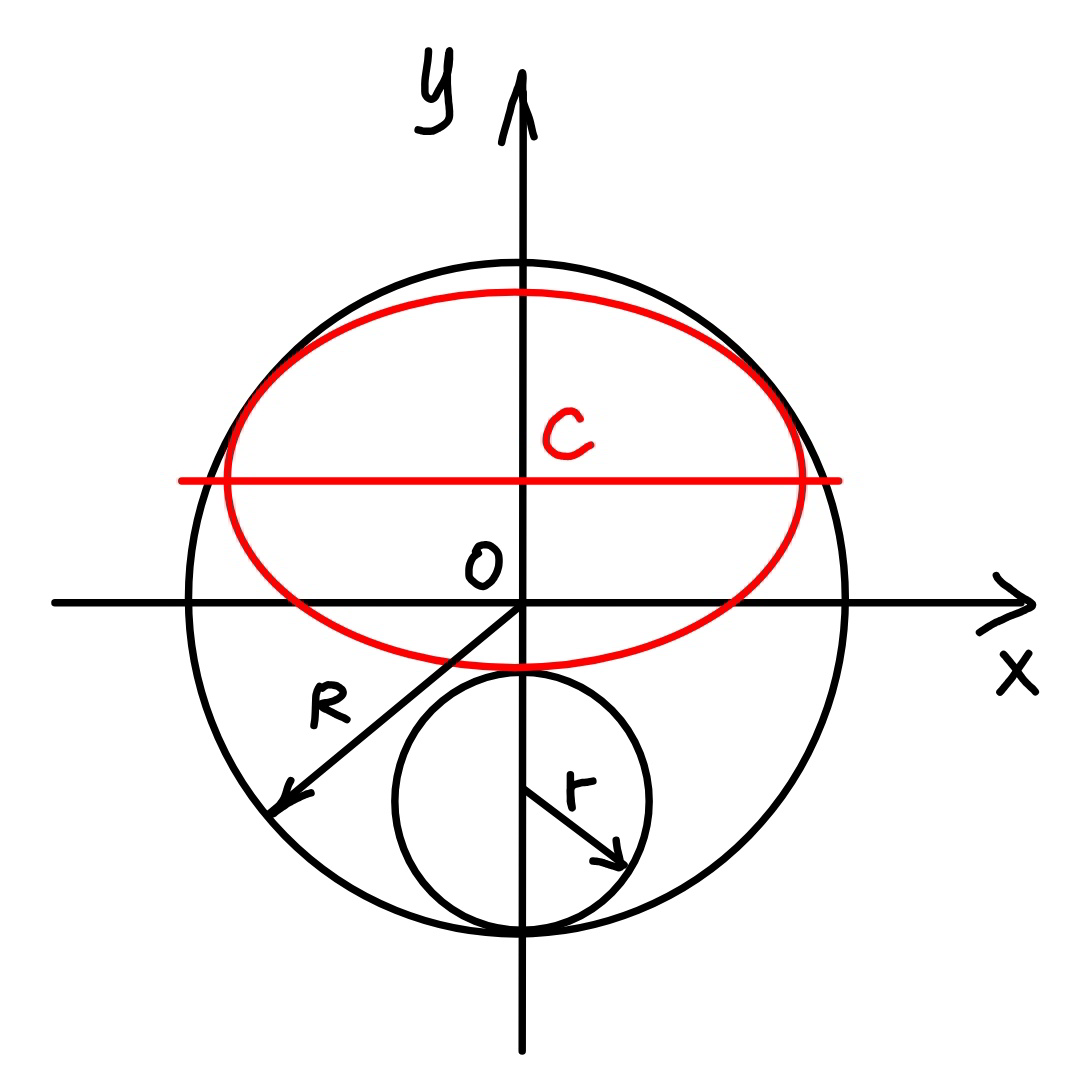
Commented by mr W last updated on 02/Feb/20
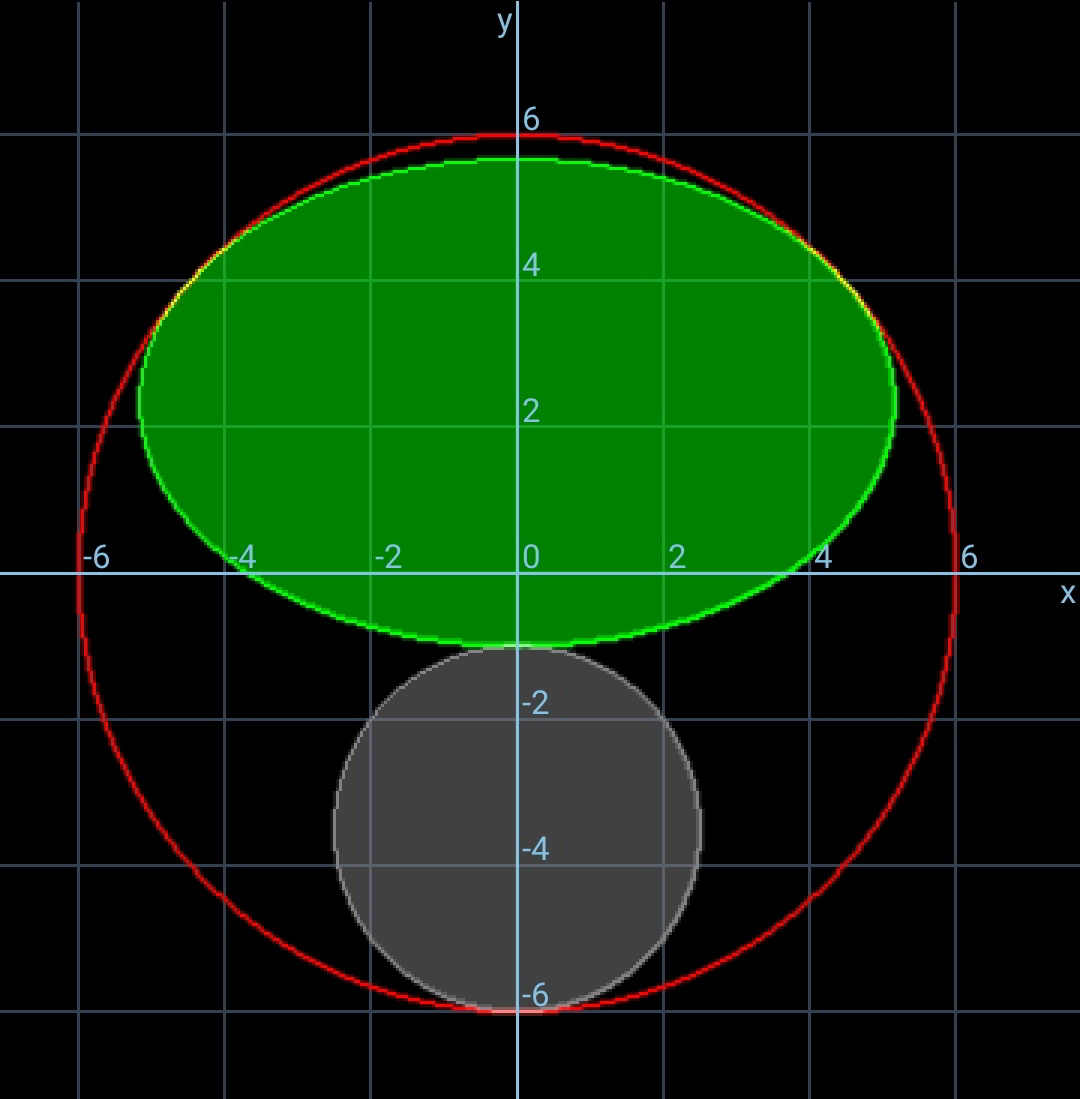
![parameters of ellipse: a, b center of ellipse: C(0,c) b−c=R−2r ⇒c=b+2r−R eqn. of big circle: x^2 +y^2 =R^2 eqn. of ellipse: (x^2 /a^2 )+(((y−c)^2 )/b^2 )=1 intersection from circle and ellipse: ((R^2 −y^2 )/a^2 )+(((y−c)^2 )/b^2 )=1 b^2 (R^2 −y^2 )+a^2 (y−c)^2 =a^2 b^2 (a^2 −b^2 )y^2 −2ca^2 y+a^2 c^2 −a^2 b^2 +R^2 b^2 =0 due to tangency Δ=0: c^2 a^4 −(a^2 −b^2 )(a^2 c^2 −a^2 b^2 +R^2 b^2 )=0 a^2 (a^2 −b^2 −R^2 +c^2 )+R^2 b^2 =0 a^4 −4r(R−r)a^2 −2(R−2r)a^2 b+R^2 b^2 =0 ⇒b=(((R−2r)a^2 +2a(√(r(R−r)(R^2 −a^2 ))))/R^2 ) let P=ab a^6 −4r(R−r)a^4 −2(R−2r)a^3 P+R^2 P^2 =0 6a^5 −16r(R−r)a^3 −2(R−2r)(3a^2 P+a^3 (dP/da))+2R^2 P(dP/da)=0 for maximum ellipse, (dP/da)=0 3a^2 −8r(R−r)=3(R−2r)b 3a^2 −2R^2 =((3(R−2r))/(2r(R−r)))a(√(r(R−r)(R^2 −a^2 ))) [9+((9(R−2r)^2 )/(4r(R−r)))]a^4 −[12+((9(R−2r)^2 )/(4r(R−r)))]R^2 a^2 +4R^4 =0 with μ=((9(R−2r)^2 )/(4r(R−r))) ⇒(9+μ)((a/R))^4 −(12+μ)((a/R))^2 +4=0 ⇒(a/R)=(√((12+μ±(√(μ(8+μ))))/(2(9+μ)))) (“+” if R>2r, “−” if R<2r)](Q80313.png)
Commented by mr W last updated on 02/Feb/20
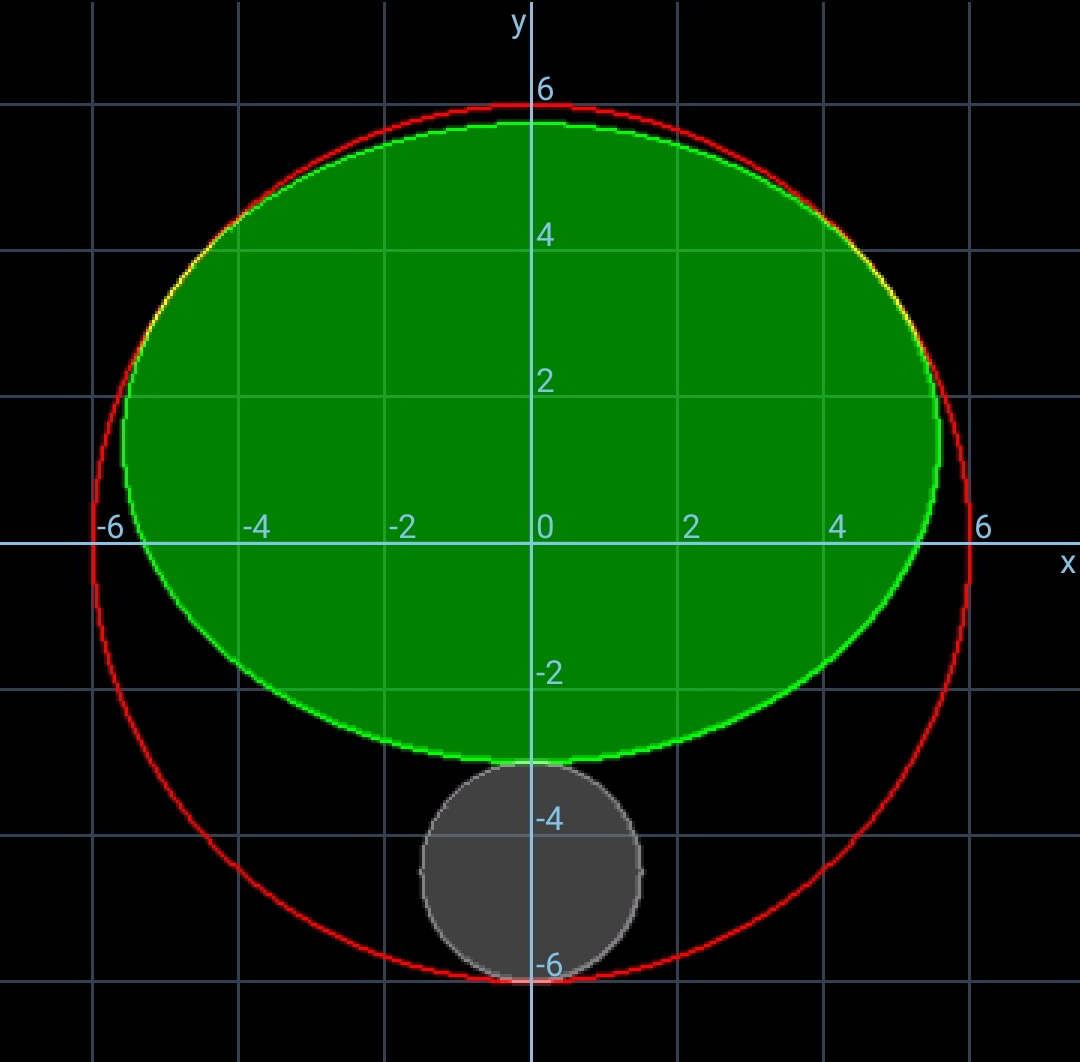
Commented by mr W last updated on 02/Feb/20
Commented by mr W last updated on 02/Feb/20