Question Number 80227 by jagoll last updated on 01/Feb/20
$${how}\:{to}\:{prove} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{x}^{{n}} \:\left(\mathrm{1}−{x}\right)^{{m}\:} \:{dx}\:=\:\frac{{m}!\:×{n}!}{\left({m}+{n}\right)!} \\ $$$${via}\:{Gamma}\:{function} \\ $$
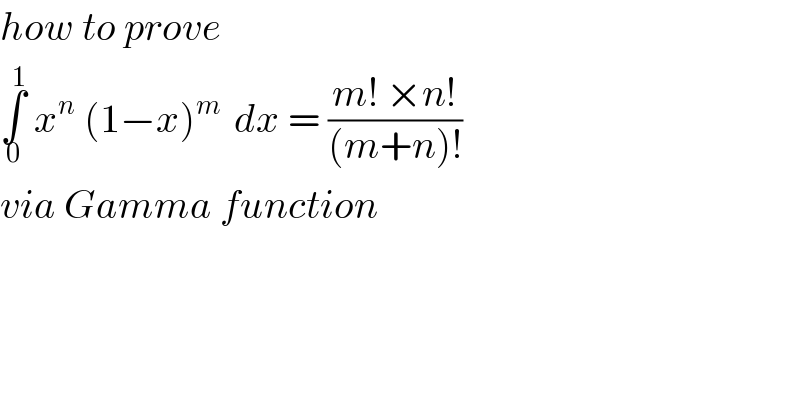
Commented by john santu last updated on 01/Feb/20
$${Beta}\:{function} \\ $$
Commented by Tony Lin last updated on 01/Feb/20
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}−{x}\right)^{{m}} {dx} \\ $$$$={B}\left({n}+\mathrm{1},\:{m}+\mathrm{1}\right) \\ $$$$=\frac{\Gamma\left({n}+\mathrm{1}\right)\Gamma\left({m}+\mathrm{1}\right)}{\Gamma\left({n}+{m}+\mathrm{2}\right)} \\ $$$$=\frac{{m}!{n}!}{\left({m}+{n}+\mathrm{1}\right)!} \\ $$
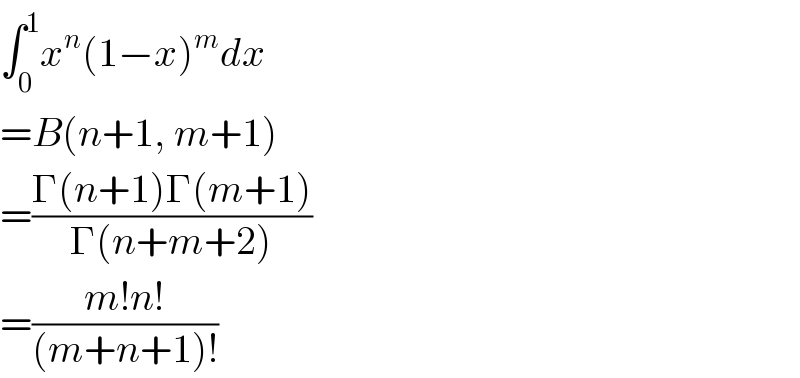
Commented by mathmax by abdo last updated on 01/Feb/20
![let A_(n,m) =∫_0 ^1 x^n (1−x)^m dx by psrts u^′ =x^n and v=(1−x)^m A_(n,m) =[(1/(n+1))x^(n+1) (1−x)^m ]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1))(−m)(1−x)^(m−1) dx =(m/(n+1)) A_(n+1,m−1) =((m(m−1))/((n+1)(n+2))) A_(n+2,m−2) = =((m(m−1)(m−2)....(m−k+1))/((n+1)(n+2)...(n+k))) A_(n+k,m−k) k=m ⇒A_(n,m) =((m!)/((n+1)(n+2)...(n+m))) A_(n+m,0) A_(n+m,0) =∫_0 ^1 x^(n+m) dx =(1/(n+m+1)) ⇒A_(n,m) =((m!)/((n+1)(n+2)....(n+m+1))) =((m!×n!)/((m+n+1)!))](Q80278.png)
$${let}\:{A}_{{n},{m}} =\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}−{x}\right)^{{m}} \:{dx}\:\:{by}\:{psrts}\:{u}^{'} ={x}^{{n}} \:{and}\:{v}=\left(\mathrm{1}−{x}\right)^{{m}} \\ $$$${A}_{{n},{m}} =\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{m}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\left(−{m}\right)\left(\mathrm{1}−{x}\right)^{{m}−\mathrm{1}} \:{dx} \\ $$$$=\frac{{m}}{{n}+\mathrm{1}}\:{A}_{{n}+\mathrm{1},{m}−\mathrm{1}} =\frac{{m}\left({m}−\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:{A}_{{n}+\mathrm{2},{m}−\mathrm{2}} = \\ $$$$=\frac{{m}\left({m}−\mathrm{1}\right)\left({m}−\mathrm{2}\right)....\left({m}−{k}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)...\left({n}+{k}\right)}\:{A}_{{n}+{k},{m}−{k}} \\ $$$${k}={m}\:\Rightarrow{A}_{{n},{m}} =\frac{{m}!}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)...\left({n}+{m}\right)}\:{A}_{{n}+{m},\mathrm{0}} \\ $$$${A}_{{n}+{m},\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}+{m}} {dx}\:=\frac{\mathrm{1}}{{n}+{m}+\mathrm{1}}\:\Rightarrow{A}_{{n},{m}} =\frac{{m}!}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)....\left({n}+{m}+\mathrm{1}\right)} \\ $$$$=\frac{{m}!×{n}!}{\left({m}+{n}+\mathrm{1}\right)!} \\ $$
Commented by mathmax by abdo last updated on 01/Feb/20
$${error}\:{in}\:{the}\:{Question}... \\ $$
Commented by mind is power last updated on 03/Feb/20
$${nice}\:{Sir} \\ $$