Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 80237 by M±th+et£s last updated on 01/Feb/20

Commented by M±th+et£s last updated on 01/Feb/20

$$ifABCDEFGisaheptagonandAB=1$$$$HIJKLMishexagon$$$$thanfindHI$$

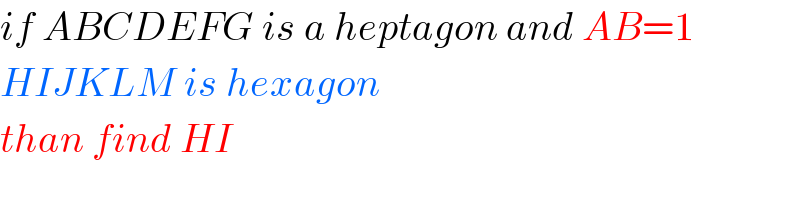
Commented by mr W last updated on 01/Feb/20

$$HIJKLMNisalsoaheptagon!$$

Commented by M±th+et£s last updated on 01/Feb/20

$$youarerightsiritstypo$$

Commented by Tony Lin last updated on 01/Feb/20

$$letIE=x$$$$\frac{x^2+x^2-1^2}{2x^2}=cos\frac{5\pi }{7}$$$$let2x^2=t$$$$\Rightarrow \frac{t-1}{t}=cos\frac{5\pi }{7}$$$$t=\frac{1}{1-cos\frac{5\pi }{7}}$$$$IH=\sqrt{x^2+x^2-2x^{2}cos\frac{3\pi }{7}}$$$$=\sqrt{t(1-cos\frac{3\pi }{7})}$$$$=\sqrt{\frac{1-cos\frac{3\pi }{7}}{1-cos\frac{5\pi }{7}}}$$

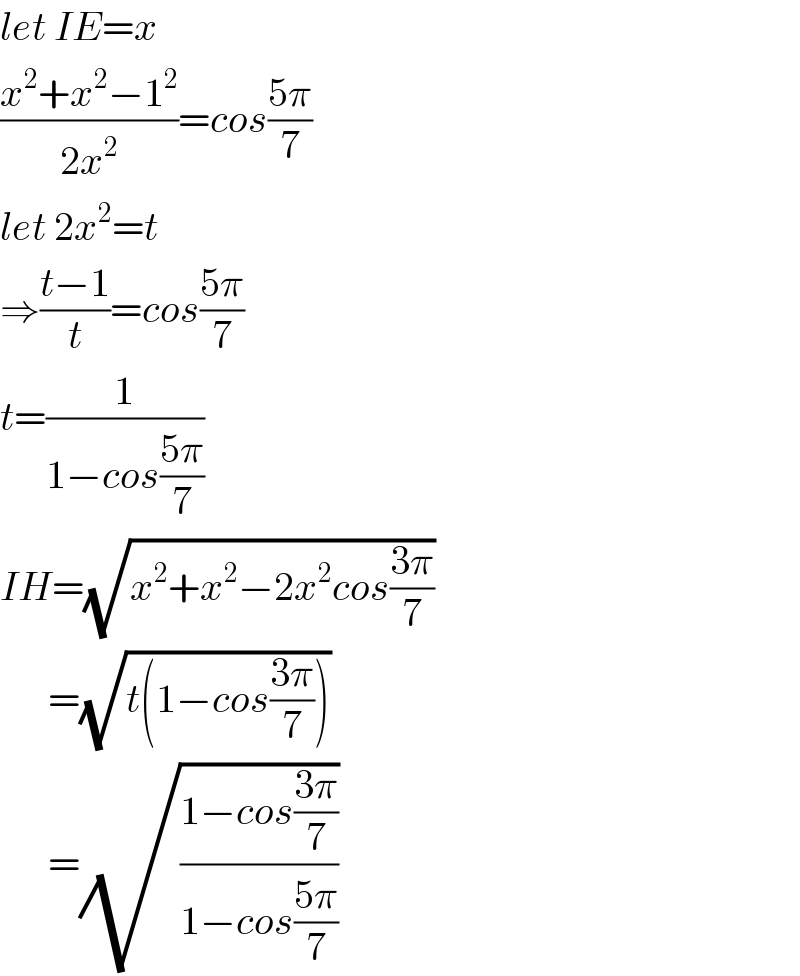
Commented by M±th+et£s last updated on 01/Feb/20

$$niceworksir$$

Answered by mr W last updated on 01/Feb/20

Commented by mr W last updated on 01/Feb/20

$$\alpha =\frac{\pi }{7}$$$$AP=AB\times \sin \alpha =\sin \alpha$$$$PL=\frac{AP}{\tan 2\alpha }=\frac{\sin \alpha }{\tan 2\alpha }$$$$HI=KL=2PL=\frac{2\sin \alpha }{\tan 2\alpha }=\frac{2\sin \frac{\pi }{7}}{\tan \frac{2\pi }{7}}\approx 0.692$$

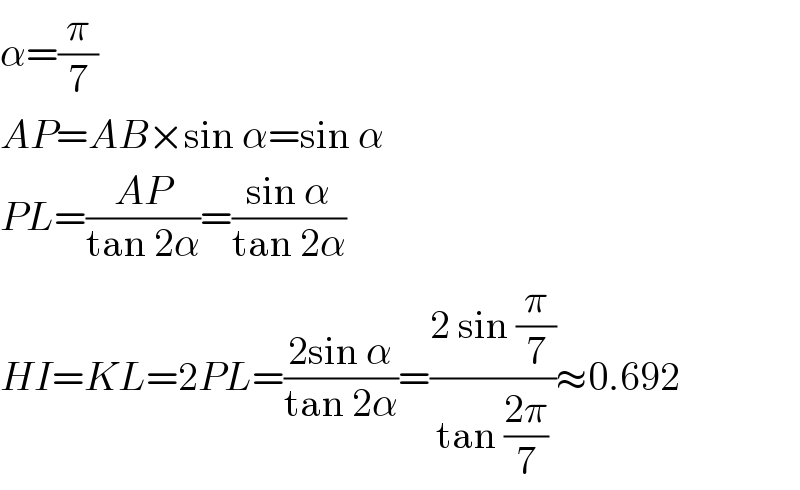
Commented by M±th+et£s last updated on 01/Feb/20

$$thankyousir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com