Question Number 80312 by TawaTawa last updated on 02/Feb/20
Commented by mr W last updated on 02/Feb/20
$${what}\:{is}\:\left\{...\right\}\:{here}\:? \\ $$
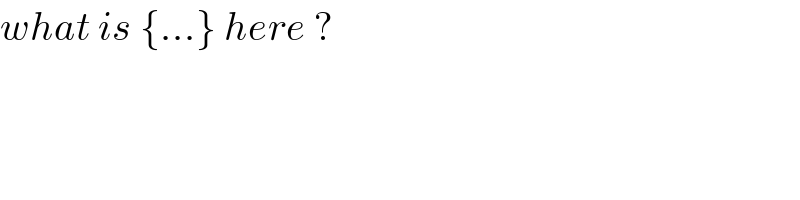
Commented by TawaTawa last updated on 02/Feb/20
$$\left(\frac{\mathrm{x}\:−\:\mathrm{1}}{\mathrm{x}\:+\:\mathrm{1}}\right)\:\mathrm{sir} \\ $$
Commented by mr W last updated on 02/Feb/20
![whether {x}=(x) or {x}=x−[x], have you ever tried to solve it by yourself?](Q80342.png)
$${whether}\:\left\{{x}\right\}=\left({x}\right)\:{or}\:\left\{{x}\right\}={x}−\left[{x}\right],\:{have} \\ $$$${you}\:{ever}\:{tried}\:{to}\:{solve}\:{it}\:{by}\:{yourself}? \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{I}\:\mathrm{did}\:\mathrm{it}\:\mathrm{like}\:\mathrm{normal}\:\mathrm{bracket}.\:\mathrm{So}\:\mathrm{i}\:\mathrm{thought}\:\mathrm{i}\:\mathrm{could}\:\mathrm{confirm}\:\mathrm{the} \\ $$$$\mathrm{answers}.\:\mathrm{But}\:\mathrm{now}\:\mathrm{it}\:\mathrm{is}\:\mathrm{different}\:\mathrm{definition}. \\ $$$$\mathrm{I}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{that}\:\mathrm{one}. \\ $$
Commented by mr W last updated on 02/Feb/20
![with {((x − 1)/(x + 1))}=(((x − 1)/(x + 1))) the question makes not much sense. i think it means fraction part, i.e. {x}=x−[x]](Q80336.png)
$${with}\:\left\{\frac{\mathrm{x}\:−\:\mathrm{1}}{\mathrm{x}\:+\:\mathrm{1}}\right\}=\left(\frac{\mathrm{x}\:−\:\mathrm{1}}{\mathrm{x}\:+\:\mathrm{1}}\right)\:{the}\:{question} \\ $$$${makes}\:{not}\:{much}\:{sense}.\:{i}\:{think}\:{it} \\ $$$${means}\:{fraction}\:{part},\:{i}.{e}. \\ $$$$\left\{{x}\right\}={x}−\left[{x}\right] \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{Maybe}\:\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{just}\:\mathrm{guess}\:\mathrm{sir}. \\ $$$$\mathrm{Since}\:\:\left\{\:\:\right\}\:\:\mathrm{has}\:\mathrm{meaning}.\:\:\mathrm{Help}\:\mathrm{me}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{Sir},\:\mathrm{it}\:\mathrm{means}\:\mathrm{the}\:\mathrm{fractional}\:\mathrm{part}. \\ $$
Commented by john santu last updated on 02/Feb/20
![{((x−1)/(x+1))}= ((x−1)/(x+1))−[((x−1)/(x+1))]=((x−1)/(x+1))−[1−(2/(x+1))] =((x−1)/(x+1))−1= ((x−1−x−1)/(x+1))=((−2)/(x+1)) ∗ Ω= ∫ (((−2)/(x+1))).((xdx)/(1−x)) = = ∫ (( 2xdx)/((x^2 −1))) = ∫ ((d(x^2 −1))/(x^2 −1)) Ω= ln(x^2 −1)+c](Q80349.png)
$$\left\{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right\}=\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}−\left[\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right]=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}−\left[\mathrm{1}−\frac{\mathrm{2}}{{x}+\mathrm{1}}\right] \\ $$$$=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}−\mathrm{1}=\:\frac{{x}−\mathrm{1}−{x}−\mathrm{1}}{{x}+\mathrm{1}}=\frac{−\mathrm{2}}{{x}+\mathrm{1}} \\ $$$$\ast\:\Omega=\:\int\:\left(\frac{−\mathrm{2}}{{x}+\mathrm{1}}\right).\frac{{xdx}}{\mathrm{1}−{x}}\:=\: \\ $$$$=\:\int\:\frac{\:\:\mathrm{2}{xdx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)}\:=\:\int\:\frac{{d}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Omega=\:{ln}\left({x}^{\mathrm{2}} −\mathrm{1}\right)+{c} \\ $$$$ \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by john santu last updated on 02/Feb/20
$${my}\:{ans}\:{is}\:{right}? \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{sir}.\:\:\mathrm{Sir}\:\:\mathrm{mrW}\:\:\mathrm{can}\:\mathrm{confirm}. \\ $$
Commented by john santu last updated on 02/Feb/20
$${ok}\:{miss}.\:{thank}\:{you}.\:{god}\:{bless}\: \\ $$$${you} \\ $$
Commented by behi83417@gmail.com last updated on 02/Feb/20
$$\Omega=\int\:\:\frac{−\mathrm{2}\boldsymbol{\mathrm{x}}\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}=−\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} −\mathrm{1}\mid+\mathrm{const}. \\ $$
Commented by mathmax by abdo last updated on 02/Feb/20
![if {((x−1)/(x+1))} means (((x−1)/(x+1))) ⇒Ω=∫_0 ^1 ((x−1)/(x+1))×((xdx)/(1−x)) =−∫_0 ^1 ((xdx)/(x+1)) =−∫_0 ^1 ((x+1−1)/(x+1))dx =−1 +∫_0 ^1 (dx/(x+1)) =−1+ln(2) if {((x−1)/(x+1))} means ((x−1)/(x+1))−[((x−1)/(x+1))] changement x=(1/t) give Ω=−∫_1 ^(+∞) {(((1/t)−1)/((1/t)+1))}×(1/(t(1−(1/t))))(−(dt/t^2 )) =∫_1 ^(+∞) {((1−t)/(1+t))}(dt/(t^2 (t−1))) =∫_1 ^(+∞) {((1−t)/(1+t))−[((1−t)/(1+t))])(dt/(t^2 (t−1))) =−∫_1 ^(+∞) (dt/(t^2 (t+1))) −∫_1 ^(+∞) [((1−t)/(1+t))](dt/(t^2 (t−1))) let decompose f(t)=(1/(t^2 (t+1))) ⇒f(t)=(a/t) +(b/t^2 ) +(c/(t+1)) b=t^2 f(t)∣_(t=0) =1 and c=(t+1)f(t)∣_(t=−1) =1 ⇒ f(t)=(a/t)+(1/(t+1)) +(1/t^2 ) f(1)=(1/2) =a+(1/2) +1 ⇒a=−1 ⇒f(t)=−(1/t)+(1/(t+1))+(1/t^2 ) ⇒ ∫_1 ^(+∞) f(t)dt =[−ln∣t∣+ln∣t+1∣−(1/t)]_1 ^(+∞) =[ln∣((t+1)/t)∣−(1/t)]_1 ^(+∞) =−ln(2)+1 also ∫_1 ^(+∞) [((1−t)/(1+t))](dt/(t^2 (t−1))) =∫_1 ^(+∞) [−((t−1)/(t+1))](dt/(t^2 (t−1))) =∫_1 ^(+∞) [−((t+1−2)/(t+1))](dt/(t^2 (t−1))) =∫_1 ^(+∞) [−1+(2/(t+1))](dt/(t^2 (t−1))) =−∫_1 ^(+∞) (dt/(t^2 (t−1))) +∫_1 ^(+∞) [(2/(t+1))](dt/(t^2 (t−1))) ∫_1 ^(+∞) (dt/(t^2 (t−1))) =_(t−1=u) ∫_0 ^(+∞) (du/(u(u+1)^(2 ) )) this integral is divergent..! also ∫_1 ^(+∞) [(2/(t+1))](dt/(t^2 (t−1))) =_(t+1=u) ∫_2 ^(+∞) [(2/u)](du/((u−1)^2 (u−2))) for u>2 ⇒0<(1/u)<(1/2) ⇒0<(2/u)<1 ⇒[(2/u)]=0 any way Ω diverges...](Q80392.png)
$${if}\:\left\{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right\}\:{means}\:\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)\:\Rightarrow\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}×\frac{{xdx}}{\mathrm{1}−{x}} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{xdx}}{{x}+\mathrm{1}}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}+\mathrm{1}−\mathrm{1}}{{x}+\mathrm{1}}{dx}\:=−\mathrm{1}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{{x}+\mathrm{1}}\:=−\mathrm{1}+{ln}\left(\mathrm{2}\right) \\ $$$${if}\:\left\{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right\}\:{means}\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}−\left[\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right]\:{changement}\:{x}=\frac{\mathrm{1}}{{t}}\:{give} \\ $$$$\Omega=−\int_{\mathrm{1}} ^{+\infty} \left\{\frac{\frac{\mathrm{1}}{{t}}−\mathrm{1}}{\frac{\mathrm{1}}{{t}}+\mathrm{1}}\right\}×\frac{\mathrm{1}}{{t}\left(\mathrm{1}−\frac{\mathrm{1}}{{t}}\right)}\left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{1}} ^{+\infty} \left\{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right\}\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}\:=\int_{\mathrm{1}} ^{+\infty} \left\{\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}−\left[\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right]\right)\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)} \\ $$$$=−\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)}\:−\int_{\mathrm{1}} ^{+\infty} \left[\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right]\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}\:{let}\:{decompose}\: \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)}\:\Rightarrow{f}\left({t}\right)=\frac{{a}}{{t}}\:+\frac{{b}}{{t}^{\mathrm{2}} }\:+\frac{{c}}{{t}+\mathrm{1}} \\ $$$${b}={t}^{\mathrm{2}} {f}\left({t}\right)\mid_{{t}=\mathrm{0}} =\mathrm{1}\:\:{and}\:{c}=\left({t}+\mathrm{1}\right){f}\left({t}\right)\mid_{{t}=−\mathrm{1}} =\mathrm{1}\:\Rightarrow \\ $$$${f}\left({t}\right)=\frac{{a}}{{t}}+\frac{\mathrm{1}}{{t}+\mathrm{1}}\:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} } \\ $$$${f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:={a}+\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{1}\:\:\Rightarrow{a}=−\mathrm{1}\:\Rightarrow{f}\left({t}\right)=−\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}}{{t}+\mathrm{1}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:{f}\left({t}\right){dt}\:=\left[−{ln}\mid{t}\mid+{ln}\mid{t}+\mathrm{1}\mid−\frac{\mathrm{1}}{{t}}\right]_{\mathrm{1}} ^{+\infty} =\left[{ln}\mid\frac{{t}+\mathrm{1}}{{t}}\mid−\frac{\mathrm{1}}{{t}}\right]_{\mathrm{1}} ^{+\infty} \\ $$$$=−{ln}\left(\mathrm{2}\right)+\mathrm{1}\:{also} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\left[\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right]\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}\:=\int_{\mathrm{1}} ^{+\infty} \left[−\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right]\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)} \\ $$$$=\int_{\mathrm{1}} ^{+\infty} \left[−\frac{{t}+\mathrm{1}−\mathrm{2}}{{t}+\mathrm{1}}\right]\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}\:=\int_{\mathrm{1}} ^{+\infty} \left[−\mathrm{1}+\frac{\mathrm{2}}{{t}+\mathrm{1}}\right]\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)} \\ $$$$=−\int_{\mathrm{1}} ^{+\infty} \frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}\:+\int_{\mathrm{1}} ^{+\infty} \:\left[\frac{\mathrm{2}}{{t}+\mathrm{1}}\right]\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}\:=_{{t}−\mathrm{1}={u}} \:\:\int_{\mathrm{0}} ^{+\infty} \:\frac{{du}}{{u}\left({u}+\mathrm{1}\right)^{\mathrm{2}\:} }\:\:{this}\:{integral}\:{is}\:{divergent}..! \\ $$$${also}\:\int_{\mathrm{1}} ^{+\infty} \left[\frac{\mathrm{2}}{{t}+\mathrm{1}}\right]\frac{{dt}}{{t}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}\:=_{{t}+\mathrm{1}={u}} \:\:\int_{\mathrm{2}} ^{+\infty} \left[\frac{\mathrm{2}}{{u}}\right]\frac{{du}}{\left({u}−\mathrm{1}\right)^{\mathrm{2}} \left({u}−\mathrm{2}\right)} \\ $$$${for}\:{u}>\mathrm{2}\:\Rightarrow\mathrm{0}<\frac{\mathrm{1}}{{u}}<\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{0}<\frac{\mathrm{2}}{{u}}<\mathrm{1}\:\Rightarrow\left[\frac{\mathrm{2}}{{u}}\right]=\mathrm{0}\:\:{any}\:{way}\:\Omega\:{diverges}... \\ $$$$ \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{I}\:\mathrm{appreciate} \\ $$
Commented by mathmax by abdo last updated on 04/Feb/20
$${you}\:{are}\:{welcome}\:. \\ $$
Answered by mr W last updated on 02/Feb/20
![{x}=x−[x] ((x−1)/(x+1))=1−(2/(x+1)) for 0≤x≤1: −1≤((x−1)/(x+1))≤0 concerning [x] for x<0 there are two different ways for the definition: way 1: [x]=⌊x⌋, i.e. [−0.5]=−1 way 2: [x]=⌈x⌉, i.e. [−0.5]=0 if we take definition way 1: since −1≤((x−1)/(x+1))≤0, {((x−1)/(x+1))}=((x−1)/(x+1))−(−1)=((2x)/(x+1)) ∫_0 ^( 1) {((x−1)/(x+1))}((xdx)/(1−x)) =∫_0 ^( 1) ((2x)/(x−1))×((xdx)/(1−x)) =−∫_0 ^( 1) ((2x^2 )/((x−1)^2 ))dx =−2∫_0 ^( 1) (((x−1+1)^2 )/((x−1)^2 ))d(x−1) =−2∫_(−1) ^( 0) (((u+1)^2 )/u^2 )du =−2∫_(−1) ^( 0) (1+(2/u)+(1/u^2 ))du =−2[u+2ln u−(1/u)]_(−1) ^0 =∞ if we take definition way 2: since −1≤((x−1)/(x+1))≤0, {((x−1)/(x+1))}=((x−1)/(x+1))−0=((x−1)/(x+1)) ∫_0 ^( 1) {((x−1)/(x+1))}((xdx)/(1−x)) =∫_0 ^( 1) ((x−1)/(x+1))×((xdx)/(1−x)) =−∫_0 ^( 1) (x/(x+1))dx =−∫_0 ^( 1) (1−(1/(x+1)))dx =−[x−ln (x+1)]_0 ^1 =ln 2−1](Q80361.png)
$$\left\{{x}\right\}={x}−\left[{x}\right] \\ $$$$\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}=\mathrm{1}−\frac{\mathrm{2}}{{x}+\mathrm{1}} \\ $$$${for}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}: \\ $$$$−\mathrm{1}\leqslant\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\leqslant\mathrm{0} \\ $$$${concerning}\:\left[{x}\right]\:{for}\:{x}<\mathrm{0}\:{there}\:{are}\:{two} \\ $$$${different}\:{ways}\:{for}\:{the}\:{definition}: \\ $$$${way}\:\mathrm{1}:\:\left[{x}\right]=\lfloor{x}\rfloor,\:{i}.{e}.\:\left[−\mathrm{0}.\mathrm{5}\right]=−\mathrm{1} \\ $$$${way}\:\mathrm{2}:\:\left[{x}\right]=\lceil{x}\rceil,\:{i}.{e}.\:\left[−\mathrm{0}.\mathrm{5}\right]=\mathrm{0} \\ $$$$ \\ $$$${if}\:{we}\:{take}\:{definition}\:{way}\:\mathrm{1}: \\ $$$${since}\:−\mathrm{1}\leqslant\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\leqslant\mathrm{0},\: \\ $$$$\:\left\{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right\}=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}−\left(−\mathrm{1}\right)=\frac{\mathrm{2}{x}}{{x}+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right\}\frac{{xdx}}{\mathrm{1}−{x}} \\ $$$$=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{2}{x}}{{x}−\mathrm{1}}×\frac{{xdx}}{\mathrm{1}−{x}} \\ $$$$=−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{2}{x}^{\mathrm{2}} }{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left({x}−\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} }{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{d}\left({x}−\mathrm{1}\right) \\ $$$$=−\mathrm{2}\int_{−\mathrm{1}} ^{\:\mathrm{0}} \frac{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{2}} }{du} \\ $$$$=−\mathrm{2}\int_{−\mathrm{1}} ^{\:\mathrm{0}} \left(\mathrm{1}+\frac{\mathrm{2}}{{u}}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\right){du} \\ $$$$=−\mathrm{2}\left[{u}+\mathrm{2ln}\:{u}−\frac{\mathrm{1}}{{u}}\right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$=\infty \\ $$$$ \\ $$$${if}\:{we}\:{take}\:{definition}\:{way}\:\mathrm{2}: \\ $$$${since}\:−\mathrm{1}\leqslant\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\leqslant\mathrm{0},\: \\ $$$$\:\left\{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right\}=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}−\mathrm{0}=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right\}\frac{{xdx}}{\mathrm{1}−{x}} \\ $$$$=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}×\frac{{xdx}}{\mathrm{1}−{x}} \\ $$$$=−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}}{{x}+\mathrm{1}}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right){dx} \\ $$$$=−\left[{x}−\mathrm{ln}\:\left({x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{ln}\:\mathrm{2}−\mathrm{1} \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 02/Feb/20
$$\mathrm{I}\:\mathrm{appreciate} \\ $$