
Question and Answers Forum
Question Number 80416 by jagoll last updated on 03/Feb/20
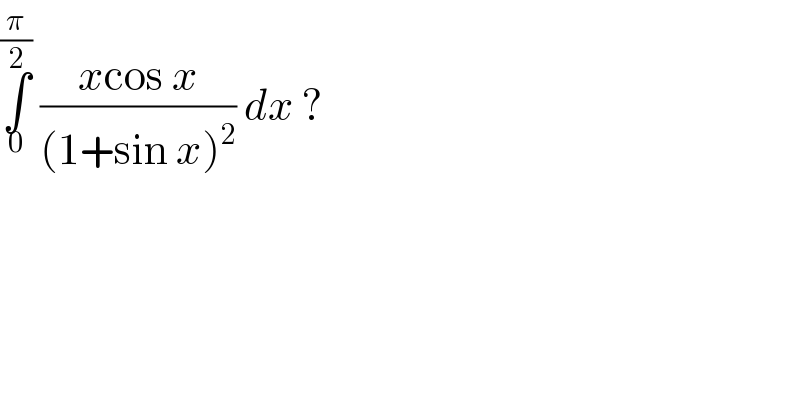
Answered by MJS last updated on 03/Feb/20
![∫((xcos x)/((1+sin x)^2 ))dx= by parts u=x → u′=1 v′=((cos x)/((1+sin x)^2 )) → v=−(1/(1+sin x)) =−(x/(1+sin x))+∫(dx/(1+sin x))= =−(x/(1+sin x))+tan x −(1/(cos x))+C ∫_0 ^(π/2) ((xcos x)/((1+sin x)^2 ))dx= [lim_(x→(π/2)) (tan x −(1/(cos x)))=0] =1−(π/4)](Q80418.png)
Commented by jagoll last updated on 03/Feb/20

Commented by jagoll last updated on 03/Feb/20
| ||
Question and Answers Forum | ||
Question Number 80416 by jagoll last updated on 03/Feb/20 | ||
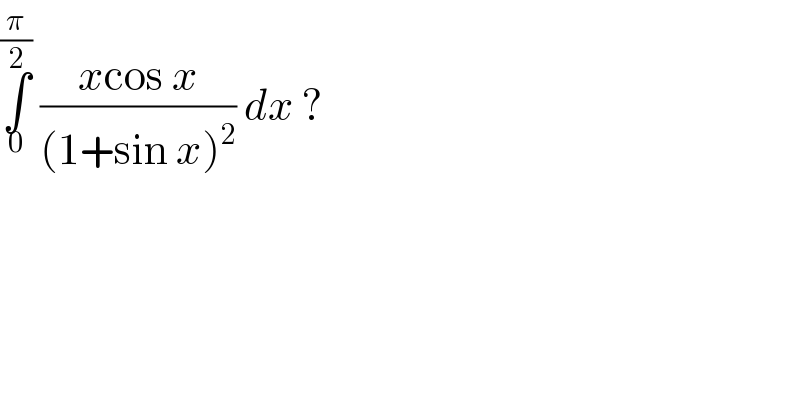 | ||
Answered by MJS last updated on 03/Feb/20 | ||
![∫((xcos x)/((1+sin x)^2 ))dx= by parts u=x → u′=1 v′=((cos x)/((1+sin x)^2 )) → v=−(1/(1+sin x)) =−(x/(1+sin x))+∫(dx/(1+sin x))= =−(x/(1+sin x))+tan x −(1/(cos x))+C ∫_0 ^(π/2) ((xcos x)/((1+sin x)^2 ))dx= [lim_(x→(π/2)) (tan x −(1/(cos x)))=0] =1−(π/4)](Q80418.png) | ||
| ||
Commented by jagoll last updated on 03/Feb/20 | ||
 | ||
Commented by jagoll last updated on 03/Feb/20 | ||
 | ||