Ψ(x)=∫_1 ^x (1/(√(1−e^t ))) dt ∀x∈R prove that Ψ(x)=2ln(((1−(√(1−e^x )))/(1−(√(1−e)))))−x+1


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 80612 by M±th+et£s last updated on 04/Feb/20

$Ψ (x) = \int_{1}^{x} \frac{1}{\sqrt{1 - e^{t}}} d t \forall x \in R$ $p r o v e t h a t$ $Ψ (x) = 2 l n (\frac{1 - \sqrt{1 - e^{x}}}{1 - \sqrt{1 - e}}) - x + 1$
Commented by mathmax by abdo last updated on 04/Feb/20

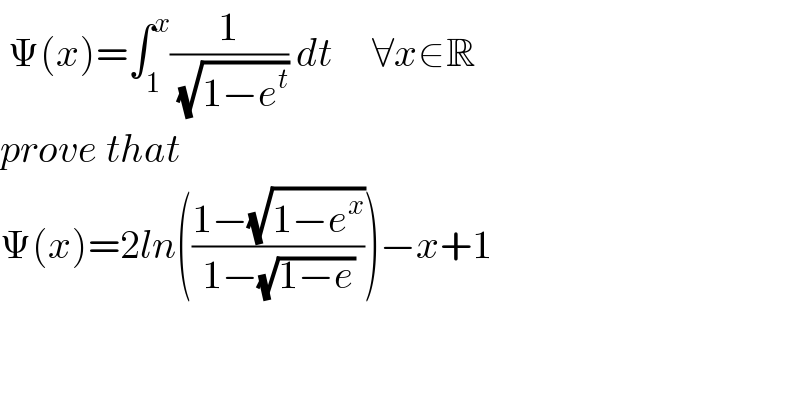
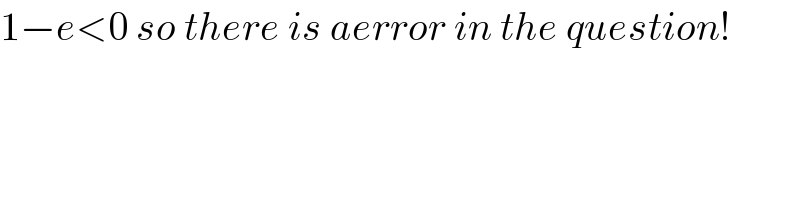
$1 - e < 0 s o t h e r e i s a e r r o r i n t h e q u e s t i o n!$
Commented by mathmax by abdo last updated on 04/Feb/20

$p e r h a p s Φ (x) = \int_{1}^{x} \frac{d t}{\sqrt{1 - e^{- t}}} o r Φ (x) = \int_{1}^{x} \frac{d t}{\sqrt{1 + e^{t}}} o r Φ (x) = \int_{1}^{x} \frac{d t}{\sqrt{1 + e^{- t}}}$
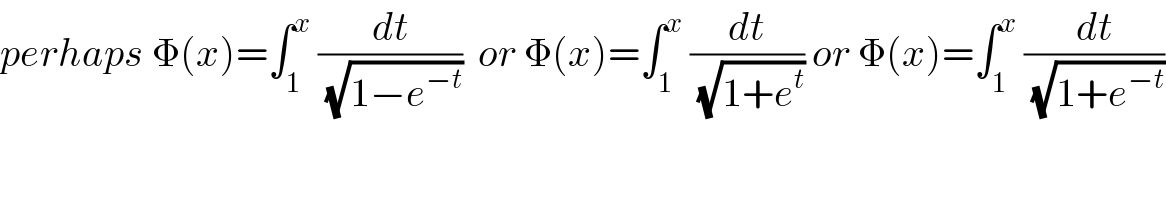
Commented by mathmax by abdo last updated on 04/Feb/20
$let take Φ(x)=∫_1 ^(x ) (dt/(√(1−e^(−t) ))) changement (√(1−e^(−t) ))=u give 1−e^(−t) =u^2 ⇒e^(−t) =1−u^2 ⇒−t=ln(1−u^2 ) ⇒t=−ln(1−u^2 ) ⇒ Φ(x)= ∫_(√(1−e^(−1) )) ^(√(1−e^(−x) )) ((2u)/((1−u^2 )u))du =2 ∫_(√(1−e^(−1) )) ^(√(1−e^(−x) )) (du/((1−u)(1+u))) =∫_(√(1−e^(−1) )) ^(√(1−e^(−x) )) {(1/(1+u))+(1/(1−u))}du=[ln∣((1+u)/(1−u))∣]_(√(1−e^(−1) )) ^(√(1−e^(−x) )) =ln∣((1+(√(1−e^(−x) )))/(1−(√(1−e^(−x) ))))∣−ln∣((1+(√(1−e^(−1) )))/(1−(√(1−e^(−1) ))))∣★$
$l e t t a k e Φ (x) = \int_{1}^{x} \frac{d t}{\sqrt{1 - e^{- t}}} c h a n g e m e n t \sqrt{1 - e^{- t}} = u g i v e$ $1 - e^{- t} = u^{2} \Rightarrow e^{- t} = 1 - u^{2} \Rightarrow - t = l n (1 - u^{2}) \Rightarrow t = - l n (1 - u^{2}) \Rightarrow$ $Φ (x) = \int_{\sqrt{1 - e^{- 1}}}^{\sqrt{1 - e^{- x}}} \frac{2 u}{(1 - u^{2}) u} d u = 2 \int_{\sqrt{1 - e^{- 1}}}^{\sqrt{1 - e^{- x}}} \frac{d u}{(1 - u) (1 + u)}$ $= \int_{\sqrt{1 - e^{- 1}}}^{\sqrt{1 - e^{- x}}} {\frac{1}{1 + u} + \frac{1}{1 - u}} d u = {[l n ∣ \frac{1 + u}{1 - u} ∣]}_{\sqrt{1 - e^{- 1}}}^{\sqrt{1 - e^{- x}}}$ $= l n ∣ \frac{1 + \sqrt{1 - e^{- x}}}{1 - \sqrt{1 - e^{- x}}} ∣ - l n ∣ \frac{1 + \sqrt{1 - e^{- 1}}}{1 - \sqrt{1 - e^{- 1}}} ∣ ★$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum