Question Number 80613 by M±th+et£s last updated on 04/Feb/20
$${Q}.{find}\:\:\:\frac{{d}}{{dx}}\left({x}!\right) \\ $$
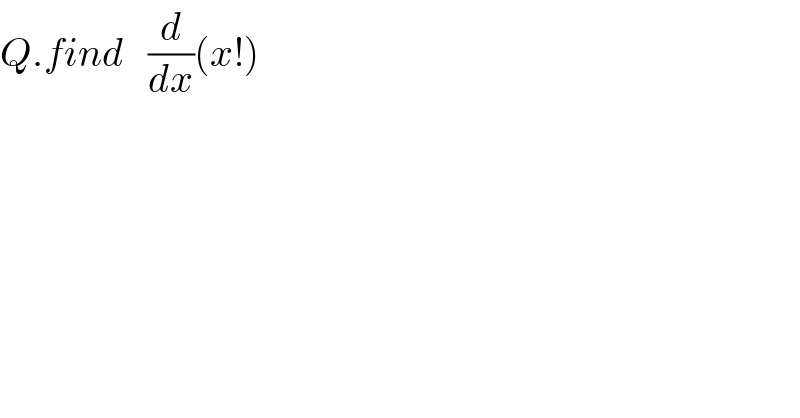
Commented by Rio Michael last updated on 04/Feb/20
$$\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{exist},\:\mathrm{from}\:\mathrm{my}\:\mathrm{understanding} \\ $$$${x}!\:=\:{x}\left({x}−\mathrm{1}\right)!\:\mathrm{has}\:\mathrm{a}\:\mathrm{domain}\:\mathrm{of}\:\mathrm{D}\:=\:{x}\:\in\:\mathbb{N}^{\ast} \\ $$$$\mathrm{tbat}\:\mathrm{means}\:\mathrm{we}\:\mathrm{have}\:\mathrm{no}\:\mathrm{specific}\:\mathrm{interval} \\ $$$$\mathrm{for}\:\mathrm{which}\:{x}!\:\mathrm{is}\:\mathrm{not}\:\mathrm{continous}\:,\:\mathrm{A}\:\mathrm{non}−\mathrm{continous}\:\mathrm{function} \\ $$$$\mathrm{is}\:\mathrm{non}−\mathrm{defferentiable}\:\mathrm{hence}\:\mathrm{i}\:\mathrm{think} \\ $$$$\frac{{d}}{{dx}}\left({x}!\right)\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{calculated}\:. \\ $$$$\mathrm{please}\:\mathrm{give}\:\mathrm{me}\:\mathrm{your}\:\mathrm{oppinion} \\ $$$$ \\ $$
Commented by MJS last updated on 04/Feb/20
![(d/dx)[x!] does not exist because x! is only defined on N ⇒ it′s not continuous Γ(x) is the extension of x! but both are not the same so if you ask for (d/dx)[x!] the correct answer is “does not exist” mathematical language is precise language x!=Γ(x+1) is true ∀x∈N but Γ(x)≠(x−1)! ∀x∈R\N](Q80637.png)
$$\frac{{d}}{{dx}}\left[{x}!\right]\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist}\:\mathrm{because}\:{x}!\:\mathrm{is}\:\mathrm{only} \\ $$$$\mathrm{defined}\:\mathrm{on}\:\mathbb{N}\:\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{continuous} \\ $$$$\Gamma\left({x}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{extension}\:\mathrm{of}\:{x}!\:\mathrm{but}\:\mathrm{both}\:\mathrm{are}\:\mathrm{not} \\ $$$$\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{so}\:\mathrm{if}\:\mathrm{you}\:\mathrm{ask}\:\mathrm{for}\:\frac{{d}}{{dx}}\left[{x}!\right]\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer} \\ $$$$\mathrm{is}\:``\mathrm{does}\:\mathrm{not}\:\mathrm{exist}'' \\ $$$$\mathrm{mathematical}\:\mathrm{language}\:\mathrm{is}\:\mathrm{precise}\:\mathrm{language} \\ $$$$ \\ $$$${x}!=\Gamma\left({x}+\mathrm{1}\right)\:\mathrm{is}\:\mathrm{true}\:\forall{x}\in\mathbb{N} \\ $$$$\mathrm{but} \\ $$$$\Gamma\left({x}\right)\neq\left({x}−\mathrm{1}\right)!\:\forall{x}\in\mathbb{R}\backslash\mathbb{N} \\ $$
Answered by M±th+et£s last updated on 04/Feb/20
![Γ(x)=(x−1)!=∫_0 ^∞ t^(x−1) e^(−t) dt ⇒(1/(Γ(x)))=xe^(γx) Π_(k=1) ^∞ (1+(x/k))e^(((−x)/k) ) ln((1/(Γ(x))))=−ln(Γ(x))=lnx+γx+Σ_(k=1) ^∞ [ln(1+(x/k))−(x/k)] (d/dx)(−ln(Γ(x)))=((Γ′(x))/(Γ(x)))=(1/x)+γ+Σ_(k=1) ^∞ [(1/(1+(x/k))).(1/k)−(1/k)] ⇒((Γ′(x))/(Γ(x)))= −(1/x)−γ+Σ_(k=1) ^∞ [(1/k)−(1/(k+x))]=Ψ(x) Ψ(x)=−γ+Σ_(k=1) ^∞ ((1/k)−(1/(k−1+x))) Ψ(x+1)=−γ+Σ_(k=1) ^∞ [(1/k)−(1/(k+x))]=((Γ′(x+1))/(Γ(x+1))) Γ′(x+1)=Ψ(x+1)Γ(x+1) (d/dx)=Γ(x+1)Ψ(x+1)](Q80625.png)
$$\Gamma\left({x}\right)=\left({x}−\mathrm{1}\right)!=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\Gamma\left({x}\right)}={xe}^{\gamma{x}} \underset{{k}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{{x}}{{k}}\right){e}^{\frac{−{x}}{{k}}\:} \\ $$$${ln}\left(\frac{\mathrm{1}}{\Gamma\left({x}\right)}\right)=−{ln}\left(\Gamma\left({x}\right)\right)={lnx}+\gamma{x}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left[{ln}\left(\mathrm{1}+\frac{{x}}{{k}}\right)−\frac{{x}}{{k}}\right] \\ $$$$\frac{{d}}{{dx}}\left(−{ln}\left(\Gamma\left({x}\right)\right)\right)=\frac{\Gamma'\left({x}\right)}{\Gamma\left({x}\right)}=\frac{\mathrm{1}}{{x}}+\gamma+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{1}+\frac{{x}}{{k}}}.\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}}\right] \\ $$$$\Rightarrow\frac{\Gamma'\left({x}\right)}{\Gamma\left({x}\right)}=\:−\frac{\mathrm{1}}{{x}}−\gamma+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+{x}}\right]=\Psi\left({x}\right) \\ $$$$\Psi\left({x}\right)=−\gamma+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}−\mathrm{1}+{x}}\right) \\ $$$$\Psi\left({x}+\mathrm{1}\right)=−\gamma+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+{x}}\right]=\frac{\Gamma'\left({x}+\mathrm{1}\right)}{\Gamma\left({x}+\mathrm{1}\right)} \\ $$$$\Gamma'\left({x}+\mathrm{1}\right)=\Psi\left({x}+\mathrm{1}\right)\Gamma\left({x}+\mathrm{1}\right) \\ $$$$\frac{{d}}{{dx}}=\Gamma\left({x}+\mathrm{1}\right)\Psi\left({x}+\mathrm{1}\right) \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 04/Feb/20
$$\Psi^{\left({m}\right)} \left({z}\right)=\left(−\mathrm{1}\right)^{{m}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} \frac{{t}^{{m}} {e}^{−{zt}} }{\mathrm{1}−{e}^{−{t}} }{dt}\::{m}>\mathrm{0}\:{and}\:{Re}\left({z}\right)>\mathrm{0} \\ $$
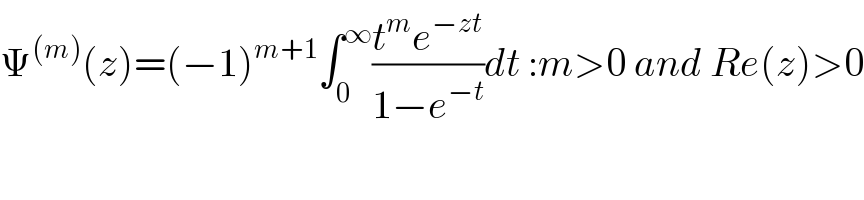
Commented by mathmax by abdo last updated on 04/Feb/20
$$\Gamma\left({x}\right)=\left({x}−\mathrm{1}\right)!\:{is}\:{only}\:{a}\:{notation}...! \\ $$