
Question and Answers Forum
Question Number 80645 by mr W last updated on 05/Feb/20
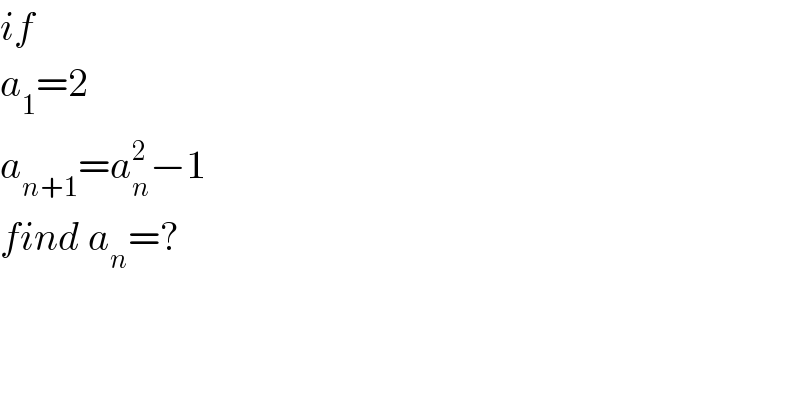
Commented by jagoll last updated on 05/Feb/20
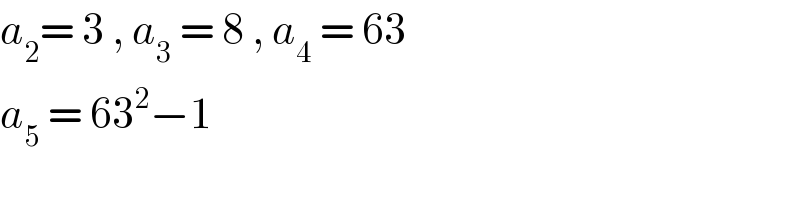
Commented by mr W last updated on 05/Feb/20
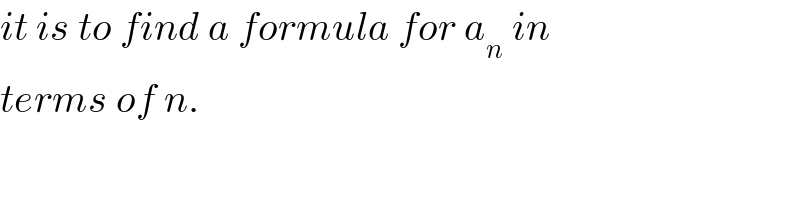
Commented by jagoll last updated on 05/Feb/20
Commented by jagoll last updated on 05/Feb/20
Commented by mind is power last updated on 05/Feb/20

Commented by mr W last updated on 06/Feb/20

Commented by jagoll last updated on 06/Feb/20

Commented by mr W last updated on 06/Feb/20

Commented by jagoll last updated on 08/Feb/20

Commented by mr W last updated on 08/Feb/20

Commented by mr W last updated on 08/Feb/20

