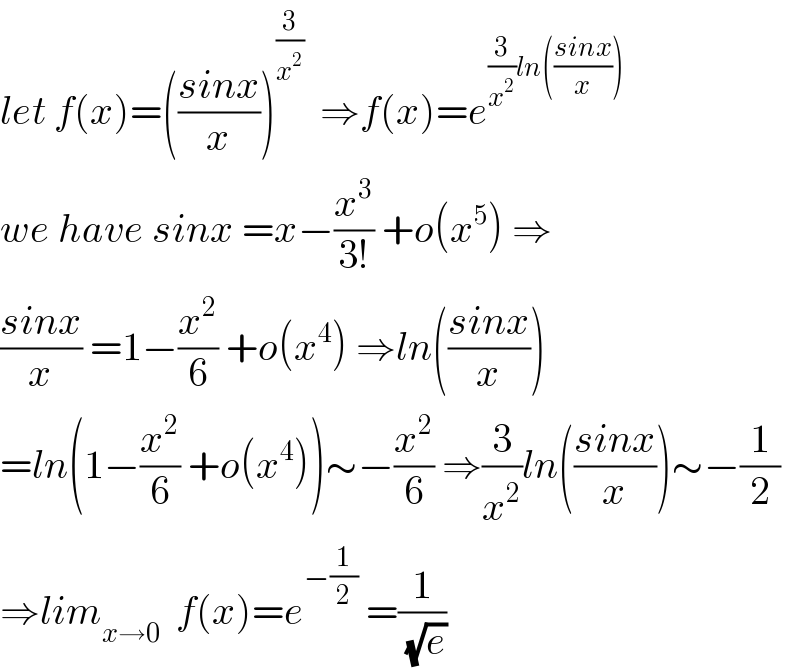Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 80653 by jagoll last updated on 05/Feb/20

lim_(x→0) (((sin x)/x))^(3/x^2 )

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }} \\ $$

Commented by john santu last updated on 05/Feb/20

lim_(x→0) (1+(((sin x)/x)−1))^(3/x^2 ) = lim_(x→0) [(1+((sin x−x)/x))^(x/(sin x−x)) ]^((3(sin x−x))/x^3 ) = e^(lim_(x→0) (((3(sin x−x))/x^3 ))) = e^(lim_(x→0) (((3(cos x−1))/(3x^2 )))) = e^(lim_(x→0) (((−sin x)/(2x)))) = e^(−(1/2)) =(1/(√e))

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\left(\frac{\mathrm{sin}\:{x}}{{x}}−\mathrm{1}\right)\right)^{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }} = \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{sin}\:{x}−{x}}{{x}}\right)^{\frac{{x}}{\mathrm{sin}\:{x}−{x}}} \right]^{\frac{\mathrm{3}\left(\mathrm{sin}\:{x}−{x}\right)}{{x}^{\mathrm{3}} }} = \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{3}\left(\mathrm{sin}\:{x}−{x}\right)}{{x}^{\mathrm{3}} }\right)} \:=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{3}\left(\mathrm{cos}\:{x}−\mathrm{1}\right)}{\mathrm{3}{x}^{\mathrm{2}} }\right)} = \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{−\mathrm{sin}\:{x}}{\mathrm{2}{x}}\right)} \:=\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\sqrt{{e}}} \\ $$

Commented by mr W last updated on 05/Feb/20

correct is (1/e^(3/6) )=(1/(√e))≈0.6065

$${correct}\:{is}\:\frac{\mathrm{1}}{{e}^{\frac{\mathrm{3}}{\mathrm{6}}} }=\frac{\mathrm{1}}{\sqrt{{e}}}\approx\mathrm{0}.\mathrm{6065} \\ $$

Commented by john santu last updated on 05/Feb/20

oo yes

$${oo}\:{yes} \\ $$

Commented by jagoll last updated on 05/Feb/20

thank you mr W and john

$${thank}\:{you}\:{mr}\:{W}\:{and}\:{john} \\ $$

Commented by abdomathmax last updated on 05/Feb/20

let f(x)=(((sinx)/x))^(3/x^2 ) ⇒f(x)=e^((3/x^2 )ln(((sinx)/x))) we have sinx =x−(x^3 /(3!)) +o(x^5 ) ⇒ ((sinx)/x) =1−(x^2 /6) +o(x^4 ) ⇒ln(((sinx)/x)) =ln(1−(x^2 /6) +o(x^4 ))∼−(x^2 /6) ⇒(3/x^2 )ln(((sinx)/x))∼−(1/2) ⇒lim_(x→0) f(x)=e^(−(1/2)) =(1/(√e))

$${let}\:{f}\left({x}\right)=\left(\frac{{sinx}}{{x}}\right)^{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }} \:\:\Rightarrow{f}\left({x}\right)={e}^{\frac{\mathrm{3}}{{x}^{\mathrm{2}} }{ln}\left(\frac{{sinx}}{{x}}\right)} \\ $$$${we}\:{have}\:{sinx}\:={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+{o}\left({x}^{\mathrm{5}} \right)\:\Rightarrow \\ $$$$\frac{{sinx}}{{x}}\:=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow{ln}\left(\frac{{sinx}}{{x}}\right) \\ $$$$={ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{4}} \right)\right)\sim−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow\frac{\mathrm{3}}{{x}^{\mathrm{2}} }{ln}\left(\frac{{sinx}}{{x}}\right)\sim−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)={e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\sqrt{{e}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com