{ (((1/x)+(1/y)=34)),(((1/(√x))+(1/(√y))=23−(1/(√(xy))) )) :} find the solution.


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 80702 by john santu last updated on 05/Feb/20

${\begin{cases} \frac{1}{x} + \frac{1}{y} = 34 \\ \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{y}} = 23 - \frac{1}{\sqrt{x y}} \end{cases}$ $f i n d t h e s o l u t i o n .$
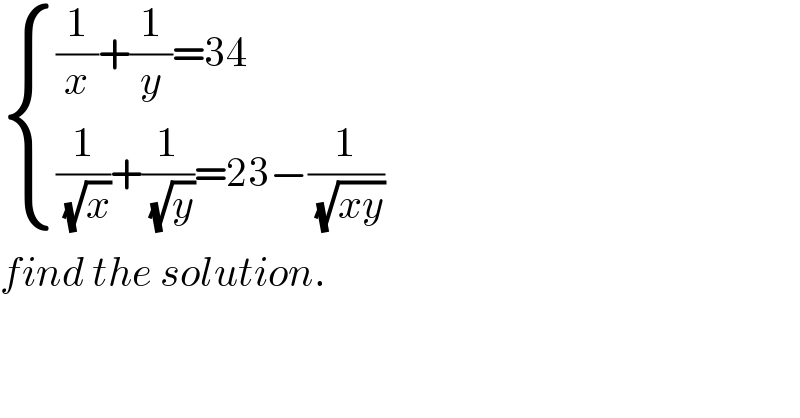
Commented by mind is power last updated on 05/Feb/20
$let (1/(√x))+(1/(√y))=u (1/(√(xy))). ⇒u^2 −2v=34 u=23−v ⇒(23−v)^2 −2v=34 v^2 −48v+495=0 v∈{15,28} u≥0⇒v=15 ⇒u=8 { (((1/(√x))+(1/(√y))=8)),(((1/(√x)).(1/(√y))=15)) :} (1/(√x)),(1/(√y)) root of X^2 −8X+15 X∈{3,5} ⇒(x,y)∈{((1/9),(1/(25)));((1/(25)),(1/9))}$
$l e t \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{y}} = u$ $\frac{1}{\sqrt{x y}} .$ $\Rightarrow u^{2} - 2 v = 34$ $u = 23 - v$ $\Rightarrow {(23 - v)}^{2} - 2 v = 34$ $v^{2} - 48 v + 495 = 0$ $v \in {15, 28}$ $u ⩾ 0 \Rightarrow v = 15 \Rightarrow u = 8$ ${\begin{cases} \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{y}} = 8 \\ \frac{1}{\sqrt{x}} . \frac{1}{\sqrt{y}} = 15 \end{cases}$ $\frac{1}{\sqrt{x}}, \frac{1}{\sqrt{y}} r o o t o f X^{2} - 8 X + 15$ $X \in {3, 5}$ $\Rightarrow (x, y) \in {(\frac{1}{9}, \frac{1}{25}); (\frac{1}{25}, \frac{1}{9})}$
Commented by john santu last updated on 05/Feb/20
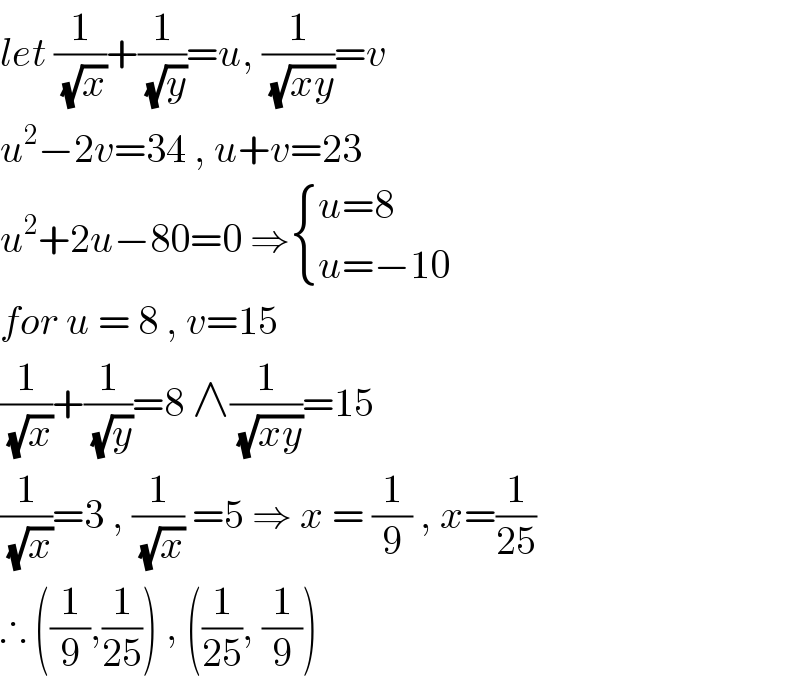
$let (1/(√x))+(1/(√y))=u, (1/(√(xy)))=v u^2 −2v=34 , u+v=23 u^2 +2u−80=0 ⇒ { ((u=8 )),((u=−10)) :} for u = 8 , v=15 (1/(√x))+(1/(√y))=8 ∧(1/(√(xy)))=15 (1/(√x))=3 , (1/(√x)) =5 ⇒ x = (1/9) , x=(1/(25)) ∴ ((1/9),(1/(25))) , ((1/(25)), (1/9))$
$l e t \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{y}} = u, \frac{1}{\sqrt{x y}} = v$ $u^{2} - 2 v = 34, u + v = 23$ $u^{2} + 2 u - 80 = 0 \Rightarrow {\begin{cases} u = 8 \\ u = - 10 \end{cases}$ $f o r u = 8, v = 15$ $\frac{1}{\sqrt{x}} + \frac{1}{\sqrt{y}} = 8 \land \frac{1}{\sqrt{x y}} = 15$ $\frac{1}{\sqrt{x}} = 3, \frac{1}{\sqrt{x}} = 5 \Rightarrow x = \frac{1}{9}, x = \frac{1}{25}$ $∴ (\frac{1}{9}, \frac{1}{25}), (\frac{1}{25}, \frac{1}{9})$
Commented by john santu last updated on 05/Feb/20

$g r e a t s i r$
Commented by MJS last updated on 06/Feb/20
$(1/(√x))=u−v; (1/(√y))=u+v; u−v>0∧u+v>0 { ((v^2 =17−u^2 )),((u^2 +u−20=0)) :} { ((v_1 =±2(√2)i; v_2 =±1)),((u_1 =−5; u_2 =4)) :} [u_1 , v_1 not useable] (1/(√x))=5∧(1/(√y))=3 ∨ (1/(√x))=3∧(1/(√y))=5 x=(1/(25))∧y=(1/9) ∨ x=(1/9)∧y=(1/(25))$
$\frac{1}{\sqrt{x}} = u - v; \frac{1}{\sqrt{y}} = u + v; u - v > 0 \land u + v > 0$ ${\begin{cases} v^{2} = 17 - u^{2} \\ u^{2} + u - 20 = 0 \end{cases}$ ${\begin{cases} v_{1} = \pm 2 \sqrt{2} i; v_{2} = \pm 1 \\ u_{1} = - 5; u_{2} = 4 \end{cases} [u_{1}, v_{1} not useable]$ $\frac{1}{\sqrt{x}} = 5 \land \frac{1}{\sqrt{y}} = 3 \lor \frac{1}{\sqrt{x}} = 3 \land \frac{1}{\sqrt{y}} = 5$ $x = \frac{1}{25} \land y = \frac{1}{9} \lor x = \frac{1}{9} \land y = \frac{1}{25}$
	Answered by behi83417@gmail.com last updated on 05/Feb/20
	$(1/x)=t^2 ,(1/y)=s^2 ⇒ { ((t^2 +s^2 =34)),((t+s=23−ts)) :}⇒_(ts=q) ^(t+s=p) { (((t+s)^2 −2ts=34)),((t+s+ts=23)) :} ⇒ { ((p^2 −2q=34)),((p+q=23)) :}⇒p^2 −2(23−p)−34=0 ⇒p^2 +2p+1=34+46+1⇒(p+1)^2 =81 ⇒p+1=±9⇒ { ((p=8⇒q=15)),((p=−10⇒q=33)) :} ⇒ { (([p=8,q=15]⇒[(1/(√x))=3,5,(1/(√y))=5,3])),((⇒(x,y)=((1/9),(1/(25))),((1/(25)),(1/9)))) :} ⇒ { (([p=−10,q=33]⇒z^2 +10z+33=0)),((z=−5±(√(25−4×33))=−5±(√(107))i)) :} ⇒(1/(√x))=−5±(√(107))i⇒ { ((x=(1/((−5−(√(107))i)^2 )))),((y=(1/((−5+(√(107))i)^2 )))) :}$
	$\frac{1}{x} = t^{2}, \frac{1}{y} = s^{2}$ $\Rightarrow {\begin{cases} t^{2} + s^{2} = 34 \\ t + s = 23 - ts \end{cases} \underset{ts = q}{\overset{t + s = p}{\Rightarrow}} {\begin{cases} {(t + s)}^{2} - 2 ts = 34 \\ t + s + ts = 23 \end{cases}$ $\Rightarrow {\begin{cases} p^{2} - 2 q = 34 \\ p + q = 23 \end{cases} \Rightarrow p^{2} - 2 (23 - p) - 34 = 0$ $\Rightarrow p^{2} + 2 p + 1 = 34 + 46 + 1 \Rightarrow {(p + 1)}^{2} = 81$ $\Rightarrow p + 1 = \pm 9 \Rightarrow {\begin{cases} p = 8 \Rightarrow q = 15 \\ p = - 10 \Rightarrow q = 33 \end{cases}$ $\Rightarrow {\begin{cases} [p = 8, q = 15] \Rightarrow [\frac{1}{\sqrt{x}} = 3, 5, \frac{1}{\sqrt{y}} = 5, 3] \\ \Rightarrow (x, y) = (\frac{1}{9}, \frac{1}{25}), (\frac{1}{25}, \frac{1}{9}) \end{cases}$ $\Rightarrow {\begin{cases} [p = - 10, q = 33] \Rightarrow z^{2} + 10 z + 33 = 0 \\ z = - 5 \pm \sqrt{25 - 4 \times 33} = - 5 \pm \sqrt{107} i \end{cases}$ $\Rightarrow \frac{1}{\sqrt{x}} = - 5 \pm \sqrt{107} i \Rightarrow {\begin{cases} x = \frac{1}{{(- 5 - \sqrt{107} i)}^{2}} \\ y = \frac{1}{{(- 5 + \sqrt{107} i)}^{2}} \end{cases}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum