Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 80977 by ajfour last updated on 08/Feb/20

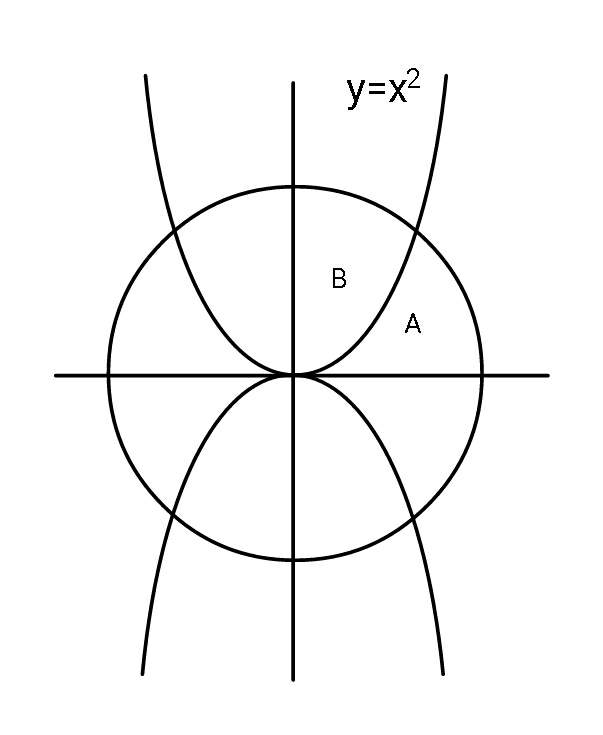
Commented by ajfour last updated on 08/Feb/20

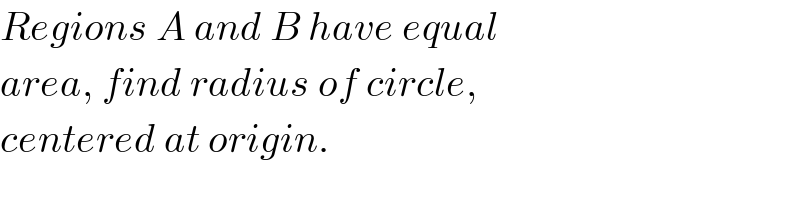
$R e g i o n s A a n d B h a v e e q u a l$ $a r e a, f i n d r a d i u s o f c i r c l e,$ $c e n t e r e d a t o r i g i n .$
Commented by ajfour last updated on 08/Feb/20

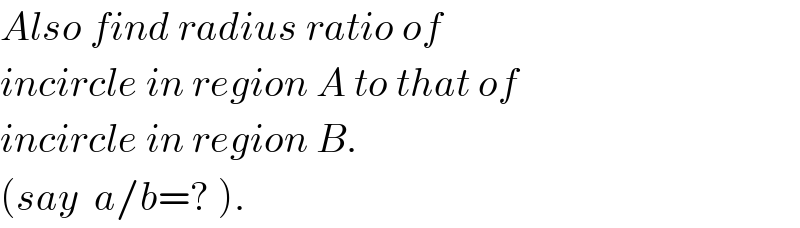
$A l s o f i n d r a d i u s r a t i o o f$ $i n c i r c l e i n r e g i o n A t o t h a t o f$ $i n c i r c l e i n r e g i o n B .$ $(s a y a / b = ?) .$
Commented by mr W last updated on 08/Feb/20

$i g o t R \approx 2.35223$
Commented by ajfour last updated on 08/Feb/20

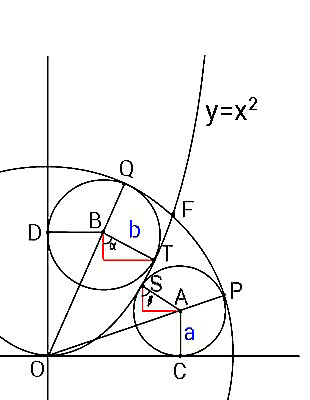
Commented by ajfour last updated on 08/Feb/20
$let F(h,h^2 ) S=∫_0 ^( h) [hx−x^2 ]dx=(h^3 /6) R=h(√(1+h^2 )) ((R^2 (tan^(−1) h))/2)−((2h^3 )/6)=(R^2 /2)((π/2)−tan^(−1) h) h^2 (1+h^2 ){tan^(−1) h−(π/4)}=(h^3 /3) ⇒ tan^(−1) h=(π/4)+(h/(3(1+h^2 ))) R=h(√(1+h^2 )) ..........$
$l e t F (h, h^{2})$ $S = \int_{0}^{h} [h x - x^{2}] d x = \frac{h^{3}}{6}$ $R = h \sqrt{1 + h^{2}}$ $\frac{R^{2} (\tan^{- 1} h)}{2} - \frac{2 h^{3}}{6} = \frac{R^{2}}{2} (\frac{π}{2} - \tan^{- 1} h)$ $h^{2} (1 + h^{2}) {\tan^{- 1} h - \frac{π}{4}} = \frac{h^{3}}{3}$ $\Rightarrow \tan^{- 1} h = \frac{π}{4} + \frac{h}{3 (1 + h^{2})}$ $R = h \sqrt{1 + h^{2}}$ $. . . . . . . . . .$
Commented by ajfour last updated on 08/Feb/20

$t h a t s r i g h t s i r, a t l e a s t i g o t t h e$ $s a m e, R \approx 2.35223015$
	Answered by mr W last updated on 08/Feb/20

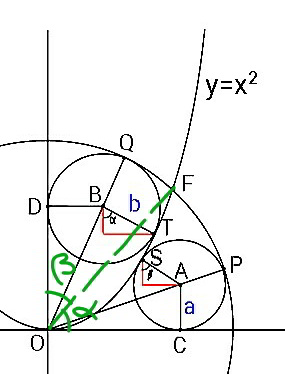
	Commented by mr W last updated on 08/Feb/20

	$F (h, h^{2})$ $R = O F = \sqrt{h^{2} + h^{4}} = h \sqrt{1 + h^{2}}$ $\tan α = \frac{h^{2}}{h} = h$ $β = \frac{π}{2} - α$ $A r e a B = \frac{2 h^{3}}{3} + \frac{R^{2}}{4} (2 β - \sin 2 β) = \frac{π R^{2}}{8}$ $\frac{16 h^{3}}{3 R^{2}} + 2 π - 4 α - 2 \sin (π - 2 α) = π$ $\frac{16 h}{3 (1 + h^{2})} + π - 4 α - 2 \sin 2 α = 0$ $\frac{16 h}{3 (1 + h^{2})} + π - 4 α - \frac{4 h}{1 + h^{2}} = 0$ $\Rightarrow \frac{h}{3 (1 + h^{2})} + \frac{π}{4} - \tan^{- 1} h = 0$ $\Rightarrow h \approx 1.380139$ $\Rightarrow R \approx 2.352230$ $T (t, t^{2})$ $(θ i s m a r k e d a s α a t B i n d i a g r a m!)$ $\tan θ = 2 t \Rightarrow t = \frac{\tan θ}{2}$ $x_{B} = t - b \sin θ = b \Rightarrow b = \frac{t}{1 + \sin θ} = \frac{\tan θ}{2 (1 + \sin θ)}$ $y_{B} = t^{2} + b \cos θ$ $x_{B}^{2} + y_{B}^{2} = {(R - b)}^{2}$ ${(t^{2} + b \cos θ)}^{2} = R (R - 2 b)$ ${(\frac{\tan^{2} θ}{4} + \frac{\sin θ}{2 (1 + \sin θ)})}^{2} = R (R - \frac{\tan θ}{1 + \sin θ})$ $\Rightarrow θ \approx 66.999803 °$ $\Rightarrow b \approx 0.613336$ $S (s, s^{2})$ $(φ i s m a r k e d a s β a t A i n d i a g r a m!)$ $\tan φ = 2 s \Rightarrow s = \frac{\tan φ}{2}$ $x_{A} = s + a \sin φ$ $y_{A} = s^{2} - a \cos φ = a \Rightarrow a = \frac{s^{2}}{1 + \cos φ} = \frac{\tan^{2} φ}{4 (1 + \cos φ)}$ $x_{A}^{2} + y_{A}^{2} = {(R - a)}^{2}$ ${(s + a \sin φ)}^{2} + a^{2} = {(R - a)}^{2}$ ${(s + a \sin φ)}^{2} = R (R - 2 a)$ $\tan^{2} φ {(1 + \frac{1}{\cos φ})}^{2} = 16 R (R - \frac{1 - \cos φ}{{2 \cos}^{2} φ})$ $\Rightarrow φ \approx 62.917105 °$ $\Rightarrow a \approx 0.656990$ $\frac{a}{b} \approx 1.071174$
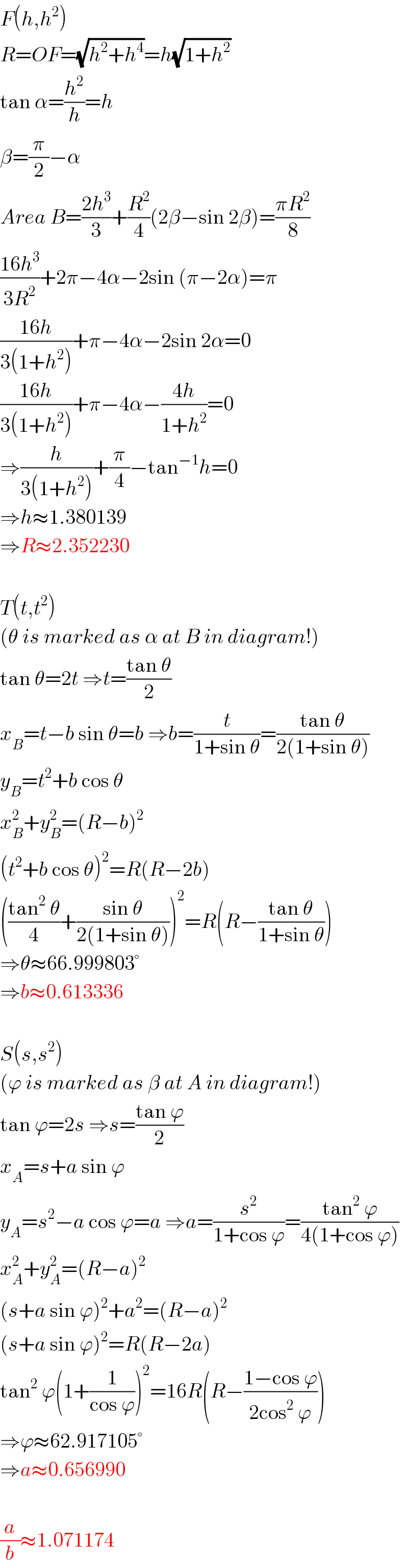
	Commented by mr W last updated on 08/Feb/20

	Commented by ajfour last updated on 08/Feb/20

	$p e r f e c t l y p e r f e c t s i r, w h a t t o$ $s a y . . . E v i d e n c e e n o u g h,$ $c o n g r a t u l a t i o n s & l o t o f t h a n k s!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum