∫ ((2e^(2x) −e^x )/(√(3e^(2x) −6e^x −1))) dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 81043 by john santu last updated on 09/Feb/20

$\int \frac{2 e^{2 x} - e^{x}}{\sqrt{3 e^{2 x} - 6 e^{x} - 1}} d x$
Commented by john santu last updated on 09/Feb/20

$u = e^{x} \Rightarrow d u = e^{x} d x$ $\int \frac{2 u - 1}{\sqrt{3 {(u - 1)}^{2} - 4}} d u =$ $\int \frac{2 u - 1}{2 \sqrt{\frac{3}{4} {(u - 1)}^{2} - 1}} d u =$ $\frac{3}{4} {(u - 1)}^{2} = \sec^{2} θ$ $\Rightarrow \int (\frac{2 . \frac{2}{\sqrt{3}} \sec θ + 1}{2 \sqrt{\sec^{2} θ - 1}}) \frac{2}{\sqrt{3}} \sec θ \tan θ d θ =$ $\int \frac{4}{3} \sec^{2} θ d θ + \int \frac{1}{\sqrt{3}} \sec θ d θ =$ $\frac{4}{3} \tan θ + \frac{1}{\sqrt{3}} l n ∣ \sec θ + \tan θ ∣ + c$ $\frac{4}{3} \sqrt{\frac{3}{4} {(e^{x} - 1)}^{2} - 1} + \frac{1}{\sqrt{3}} l n ∣ \frac{\sqrt{3}}{2} (e^{x} - 1) + \sqrt{\frac{3}{4} {(e^{x} - 1)}^{2} - 1} ∣ + c$
Commented by john santu last updated on 09/Feb/20

$m a y b e s o m e o n e k n o w s a n o t h e r w a y ?$
Commented by peter frank last updated on 09/Feb/20

$s i r t h e f i r s t l i n e 2 u^{2} - u$
Commented by john santu last updated on 09/Feb/20

$t h e s a m e s i r t o 2 u - 1$
Commented by abdomathmax last updated on 09/Feb/20
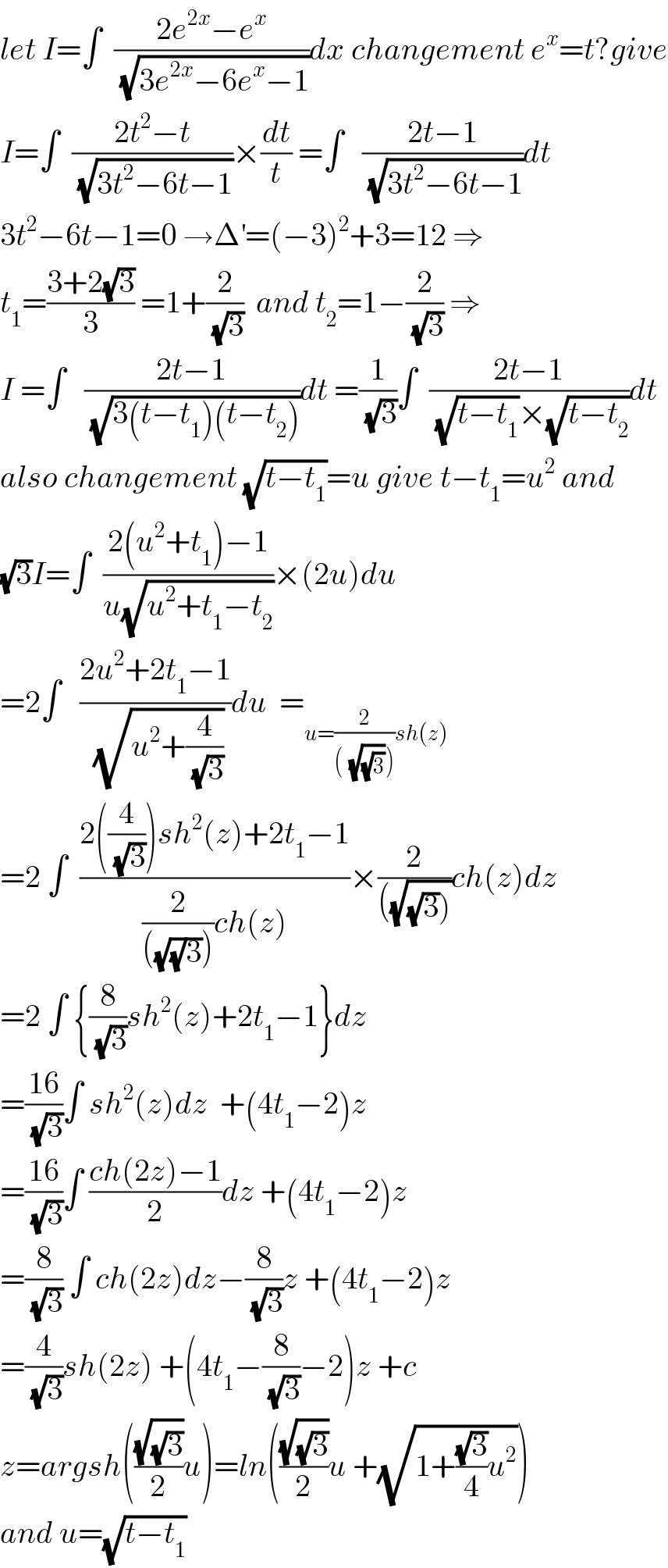
$let I=∫ ((2e^(2x) −e^x )/(√(3e^(2x) −6e^x −1)))dx changement e^x =t?give I=∫ ((2t^2 −t)/(√(3t^2 −6t−1)))×(dt/t) =∫ ((2t−1)/(√(3t^2 −6t−1)))dt 3t^2 −6t−1=0 →Δ^′ =(−3)^2 +3=12 ⇒ t_1 =((3+2(√3))/3) =1+(2/(√3)) and t_2 =1−(2/(√3)) ⇒ I =∫ ((2t−1)/(√(3(t−t_1 )(t−t_2 ))))dt =(1/(√3))∫ ((2t−1)/((√(t−t_1 ))×(√(t−t_2 ))))dt also changement (√(t−t_1 ))=u give t−t_1 =u^2 and (√3)I=∫ ((2(u^2 +t_1 )−1)/(u(√(u^2 +t_1 −t_2 ))))×(2u)du =2∫ ((2u^2 +2t_1 −1)/(√(u^2 +(4/(√3)))))du =_(u=(2/((^ (√(√3)))))sh(z)) =2 ∫ ((2((4/(√3)))sh^2 (z)+2t_1 −1)/((2/(((√((√)3)))))ch(z)))×(2/(((√((√3))))))ch(z)dz =2 ∫ {(8/(√3))sh^2 (z)+2t_1 −1}dz =((16)/(√3))∫ sh^2 (z)dz +(4t_1 −2)z =((16)/(√3))∫ ((ch(2z)−1)/2)dz +(4t_1 −2)z =(8/(√3)) ∫ ch(2z)dz−(8/(√3))z +(4t_1 −2)z =(4/(√3))sh(2z) +(4t_1 −(8/(√3))−2)z +c z=argsh(((√(√3))/2)u)=ln(((√(√3))/2)u +(√(1+((√3)/4)u^2 ))) and u=(√(t−t_1 ))$
$l e t I = \int \frac{2 e^{2 x} - e^{x}}{\sqrt{3 e^{2 x} - 6 e^{x} - 1}} d x c h a n g e m e n t e^{x} = t ? g i v e$ $I = \int \frac{2 t^{2} - t}{\sqrt{3 t^{2} - 6 t - 1}} \times \frac{d t}{t} = \int \frac{2 t - 1}{\sqrt{3 t^{2} - 6 t - 1}} d t$ $3 t^{2} - 6 t - 1 = 0 \to Δ^{^{'}} = {(- 3)}^{2} + 3 = 12 \Rightarrow$ $t_{1} = \frac{3 + 2 \sqrt{3}}{3} = 1 + \frac{2}{\sqrt{3}} a n d t_{2} = 1 - \frac{2}{\sqrt{3}} \Rightarrow$ $I = \int \frac{2 t - 1}{\sqrt{3 (t - t_{1}) (t - t_{2})}} d t = \frac{1}{\sqrt{3}} \int \frac{2 t - 1}{\sqrt{t - t_{1}} \times \sqrt{t - t_{2}}} d t$ $a l s o c h a n g e m e n t \sqrt{t - t_{1}} = u g i v e t - t_{1} = u^{2} a n d$ $\sqrt{3} I = \int \frac{2 (u^{2} + t_{1}) - 1}{u \sqrt{u^{2} + t_{1} - t_{2}}} \times (2 u) d u$ $= 2 \int \frac{2 u^{2} + 2 t_{1} - 1}{\sqrt{u^{2} + \frac{4}{\sqrt{3}}}} d u =_{u = \frac{2}{(^{} \sqrt{\sqrt{3}})} s h (z)}$ $= 2 \int \frac{2 (\frac{4}{\sqrt{3}}) {s h}^{2} (z) + 2 t_{1} - 1}{\frac{2}{(\sqrt{\sqrt{} 3})} c h (z)} \times \frac{2}{(\sqrt{\sqrt{3})}} c h (z) d z$ $= 2 \int {\frac{8}{\sqrt{3}} {s h}^{2} (z) + 2 t_{1} - 1} d z$ $= \frac{16}{\sqrt{3}} \int {s h}^{2} (z) d z + (4 t_{1} - 2) z$ $= \frac{16}{\sqrt{3}} \int \frac{c h (2 z) - 1}{2} d z + (4 t_{1} - 2) z$ $= \frac{8}{\sqrt{3}} \int c h (2 z) d z - \frac{8}{\sqrt{3}} z + (4 t_{1} - 2) z$ $= \frac{4}{\sqrt{3}} s h (2 z) + (4 t_{1} - \frac{8}{\sqrt{3}} - 2) z + c$ $z = a r g s h (\frac{\sqrt{\sqrt{3}}}{2} u) = l n (\frac{\sqrt{\sqrt{3}}}{2} u + \sqrt{1 + \frac{\sqrt{3}}{4} u^{2}})$ $a n d u = \sqrt{t - t_{1}}$
Commented by jagoll last updated on 09/Feb/20

$w h a t i s a r g s h s i r ?$ $\sinh^{- 1} ?$
Commented by Rio Michael last updated on 09/Feb/20

$sure$
Commented by msup trace by abdo last updated on 09/Feb/20

$y e s$
	Answered by Rio Michael last updated on 09/Feb/20

	$let u = e^{x} \Rightarrow d u = e^{x} d x$ $\int \frac{2 e^{2 x} - e^{x}}{\sqrt{3 e^{2 x} - 6 e^{x} - 1}} d x = \int \frac{2 e^{x} - 1}{\sqrt{3 e^{2 x} - 6 e^{x} - 1}} e^{x} d x$ $= \int \frac{2 u - 1}{\sqrt{3 u^{2} - 6 u - 1}} d u$ $= \int \frac{2 u}{\sqrt{3 u^{2} - 6 u - 1}} d u (p l e a s e h e l p m e e v a l u a t e t h i s)$ $- \int \frac{1}{\sqrt{3 u^{2} - 6 u - 1}} d u = - \int \frac{1}{\sqrt{3 {(u - 1)}^{2} - 4}} d u = - \frac{1}{\sqrt{3}} a r c o s h (\frac{u - 1}{2}) + k$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum