Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 8127 by Yozzia last updated on 30/Sep/16

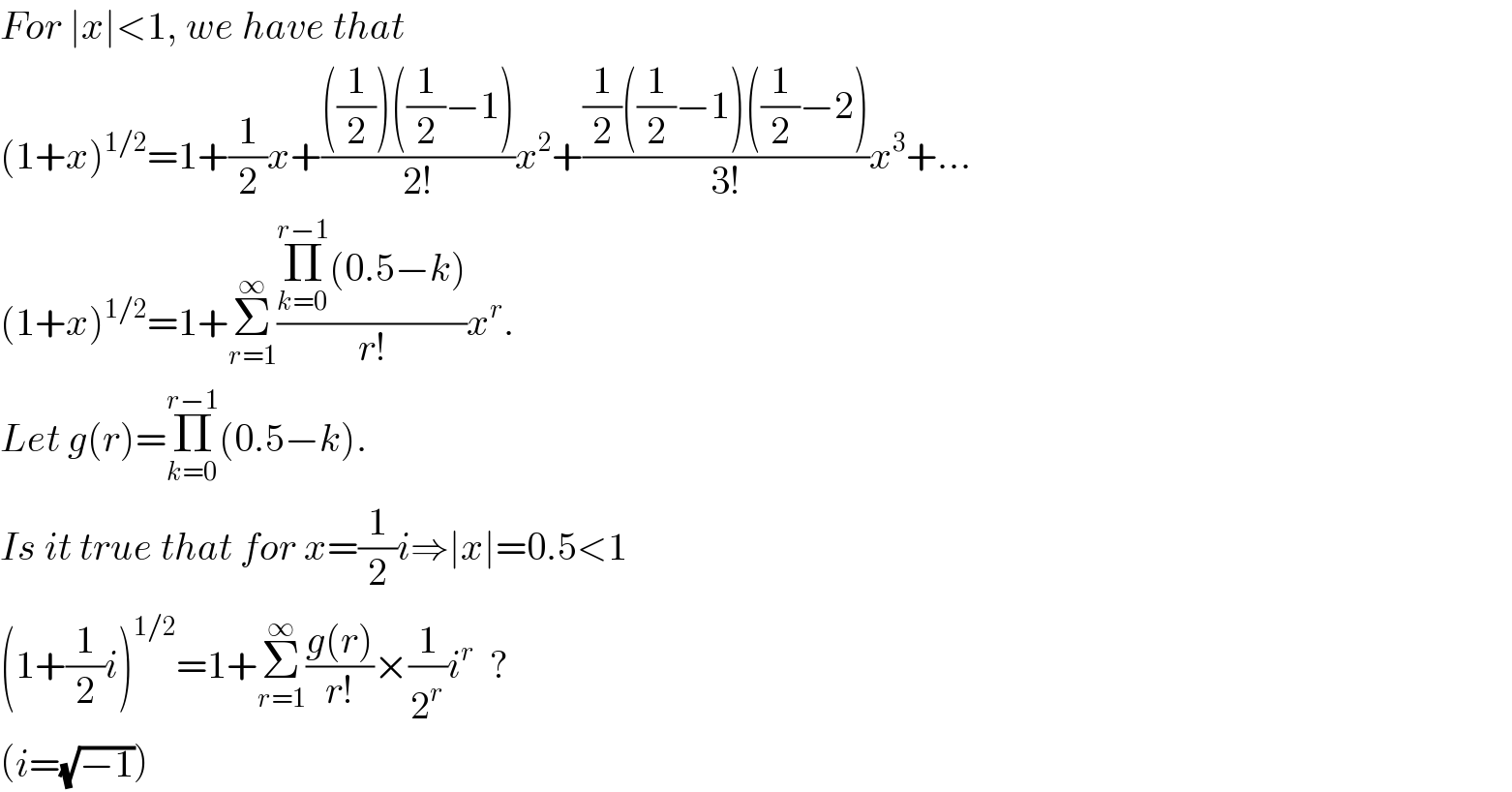
For ∣x∣<1, we have that (1+x)^(1/2) =1+(1/2)x+((((1/2))((1/2)−1))/(2!))x^2 +(((1/2)((1/2)−1)((1/2)−2))/(3!))x^3 +... (1+x)^(1/2) =1+Σ_(r=1) ^∞ ((Π_(k=0) ^(r−1) (0.5−k))/(r!))x^r . Let g(r)=Π_(k=0) ^(r−1) (0.5−k). Is it true that for x=(1/2)i⇒∣x∣=0.5<1 (1+(1/2)i)^(1/2) =1+Σ_(r=1) ^∞ ((g(r))/(r!))×(1/2^r )i^r ? (i=(√(−1)))

$${For}\:\mid{x}\mid<\mathrm{1},\:{we}\:{have}\:{that} \\ $$ $$\left(\mathrm{1}+{x}\right)^{\mathrm{1}/\mathrm{2}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} +... \\ $$ $$\left(\mathrm{1}+{x}\right)^{\mathrm{1}/\mathrm{2}} =\mathrm{1}+\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\underset{{k}=\mathrm{0}} {\overset{{r}−\mathrm{1}} {\prod}}\left(\mathrm{0}.\mathrm{5}−{k}\right)}{{r}!}{x}^{{r}} . \\ $$ $${Let}\:{g}\left({r}\right)=\underset{{k}=\mathrm{0}} {\overset{{r}−\mathrm{1}} {\prod}}\left(\mathrm{0}.\mathrm{5}−{k}\right). \\ $$ $${Is}\:{it}\:{true}\:{that}\:{for}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}{i}\Rightarrow\mid{x}\mid=\mathrm{0}.\mathrm{5}<\mathrm{1} \\ $$ $$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{i}\right)^{\mathrm{1}/\mathrm{2}} =\mathrm{1}+\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{g}\left({r}\right)}{{r}!}×\frac{\mathrm{1}}{\mathrm{2}^{{r}} }{i}^{{r}} \:\:? \\ $$ $$\left({i}=\sqrt{−\mathrm{1}}\right) \\ $$

Commented byprakash jain last updated on 01/Oct/16

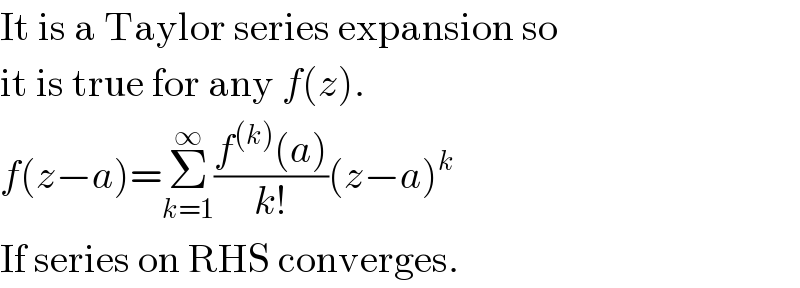
It is a Taylor series expansion so it is true for any f(z). f(z−a)=Σ_(k=1) ^∞ ((f^((k)) (a))/(k!))(z−a)^k If series on RHS converges.

$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{Taylor}\:\mathrm{series}\:\mathrm{expansion}\:\mathrm{so} \\ $$ $$\mathrm{it}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{any}\:{f}\left({z}\right). \\ $$ $${f}\left({z}−{a}\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{f}^{\left({k}\right)} \left({a}\right)}{{k}!}\left({z}−{a}\right)^{{k}} \\ $$ $$\mathrm{If}\:\mathrm{series}\:\mathrm{on}\:\mathrm{RHS}\:\mathrm{converges}. \\ $$

Commented byprakash jain last updated on 01/Oct/16

f(z)=Σ_(n=0) ^∞ c_n (z−a)^n from ratio test lim_(n→∞) ∣((c_(n+1) (z−a))/c_n )∣<1 or ∣z−a∣<lim_(n→∞) ∣(c_n /c_(n+1) )∣ for (1+z)^y (a=0) c_n =((y(y−1)...(y−n+1))/(n!)) c_(n+1) =((y(y−1)...(y−n+1)(y−n))/((n+1)!)) (c_n /c_(n+1) )=((n+1)/(y−n)) lim_(n→∞) ∣(c_n /c_(n+1) )∣=1 so the series converges if ∣z∣<1 so the series expansion of (1+(i/2))^(1/2) is correct.

$${f}\left({z}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{c}_{{n}} \left({z}−{a}\right)^{{n}} \\ $$ $${from}\:{ratio}\:{test} \\ $$ $$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\mid\frac{{c}_{{n}+\mathrm{1}} \left({z}−{a}\right)}{{c}_{{n}} }\mid<\mathrm{1} \\ $$ $$\mathrm{or}\:\mid{z}−{a}\mid<\underset{{n}\rightarrow\infty} {\mathrm{lim}}\mid\frac{{c}_{{n}} }{{c}_{{n}+\mathrm{1}} }\mid \\ $$ $$\mathrm{for}\:\left(\mathrm{1}+{z}\right)^{{y}} \:\left({a}=\mathrm{0}\right) \\ $$ $${c}_{{n}} =\frac{{y}\left({y}−\mathrm{1}\right)...\left({y}−{n}+\mathrm{1}\right)}{{n}!} \\ $$ $${c}_{{n}+\mathrm{1}} =\frac{{y}\left({y}−\mathrm{1}\right)...\left({y}−{n}+\mathrm{1}\right)\left({y}−{n}\right)}{\left({n}+\mathrm{1}\right)!} \\ $$ $$\frac{{c}_{{n}} }{{c}_{{n}+\mathrm{1}} }=\frac{{n}+\mathrm{1}}{{y}−{n}} \\ $$ $$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mid\frac{{c}_{{n}} }{{c}_{{n}+\mathrm{1}} }\mid=\mathrm{1} \\ $$ $${so}\:{the}\:{series}\:{converges}\:{if}\:\mid{z}\mid<\mathrm{1} \\ $$ $$\mathrm{so}\:\mathrm{the}\:\mathrm{series}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+\frac{{i}}{\mathrm{2}}\right)^{\mathrm{1}/\mathrm{2}} \\ $$ $$\mathrm{is}\:\mathrm{correct}. \\ $$

Commented byYozzias last updated on 01/Oct/16

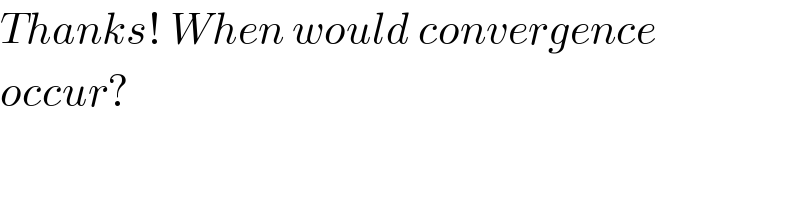
Thanks! When would convergence occur?

$${Thanks}!\:{When}\:{would}\:{convergence} \\ $$ $${occur}? \\ $$

Answered by prakash jain last updated on 02/Oct/16

answer in comments

$$\mathrm{answer}\:\mathrm{in}\:\mathrm{comments} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com