Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 81290 by mind is power last updated on 11/Feb/20

∫_(−1) ^1 arctan(x)arctan((x/(√(1−x^2 ))))arctan(((1+x)/(1−x)))dx

$$\int_{−\mathrm{1}} ^{\mathrm{1}} {arctan}\left({x}\right){arctan}\left(\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right){arctan}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right){dx} \\ $$

Commented by msup trace by abdo last updated on 11/Feb/20

changement x=−t give I=−∫_(−1) ^1 (−arctsnt)(−arctan((t/(√(1−t^2 )))))arctan(((1−t)/(1+t)))(−dt =∫_(−1) ^1 arctan(t)arctan((t/(√(1−t^2 ))))arctan(((1−t)/(1+t)))dt =∫_(−1) ^1 arctant(t)arctan((t/(√(1−t^2 ))))((π/2)−arctan)(((1+t)/(1−t)))dt =(π/2)∫_(−1) ^1 arctan(t)arctan((t/(√(1−t^2 ))))dt−I ⇒2I=(π/2) ∫_(−1) ^1 arctsn(t)arctan((t/(√(1−t^2 ))))dt ⇒I=(π/4) ∫_(−1) ^1 arctan(t)arctan((t/(√(1−t^2 ))))dt =(π/2) ∫_0 ^1 arctan(t)arctan((t/(√(1−t^2 ))))dt

$${changement}\:{x}=−{t}\:{give} \\ $$$${I}=−\int_{−\mathrm{1}} ^{\mathrm{1}} \left(−{arctsnt}\right)\left(−{arctan}\left(\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right)\right){arctan}\left(\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right)\left(−{dt}\right. \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \:{arctan}\left({t}\right){arctan}\left(\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right){arctan}\left(\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right){dt} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \:{arctant}\left({t}\right){arctan}\left(\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right)\left(\frac{\pi}{\mathrm{2}}−{arctan}\right)\left(\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\right){dt} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \:{arctan}\left({t}\right){arctan}\left(\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right){dt}−{I} \\ $$$$\Rightarrow\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:{arctsn}\left({t}\right){arctan}\left(\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right){dt} \\ $$$$\Rightarrow{I}=\frac{\pi}{\mathrm{4}}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:{arctan}\left({t}\right){arctan}\left(\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right){dt} \\ $$$$=\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({t}\right){arctan}\left(\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right){dt} \\ $$$$ \\ $$

Commented by msup trace by abdo last updated on 11/Feb/20

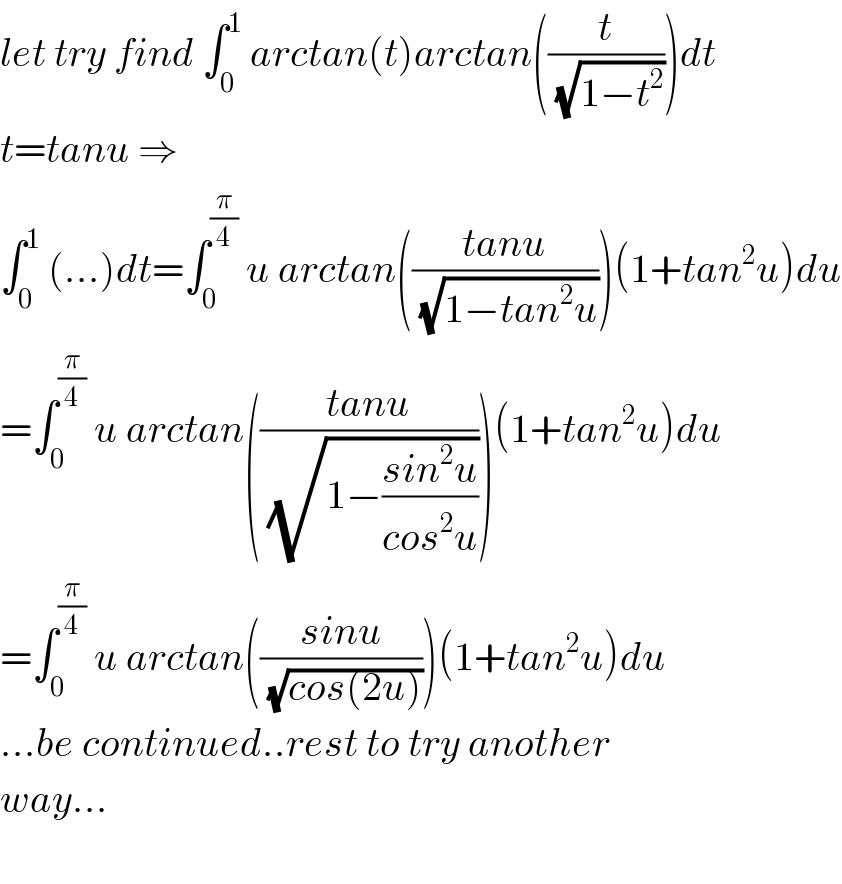
let try find ∫_0 ^1 arctan(t)arctan((t/(√(1−t^2 ))))dt t=tanu ⇒ ∫_0 ^1 (...)dt=∫_0 ^(π/4) u arctan(((tanu)/(√(1−tan^2 u))))(1+tan^2 u)du =∫_0 ^(π/4) u arctan(((tanu)/(√(1−((sin^2 u)/(cos^2 u))))))(1+tan^2 u)du =∫_0 ^(π/4) u arctan(((sinu)/(√(cos(2u)))))(1+tan^2 u)du ...be continued..rest to try another way...

$${let}\:{try}\:{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({t}\right){arctan}\left(\frac{{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right){dt} \\ $$$${t}={tanu}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(...\right){dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{u}\:{arctan}\left(\frac{{tanu}}{\sqrt{\mathrm{1}−{tan}^{\mathrm{2}} {u}}}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {u}\right){du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{u}\:{arctan}\left(\frac{{tanu}}{\sqrt{\mathrm{1}−\frac{{sin}^{\mathrm{2}} {u}}{{cos}^{\mathrm{2}} {u}}}}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {u}\right){du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{u}\:{arctan}\left(\frac{{sinu}}{\sqrt{{cos}\left(\mathrm{2}{u}\right)}}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {u}\right){du} \\ $$$$...{be}\:{continued}..{rest}\:{to}\:{try}\:{another} \\ $$$${way}... \\ $$$$ \\ $$

Commented by mind is power last updated on 11/Feb/20

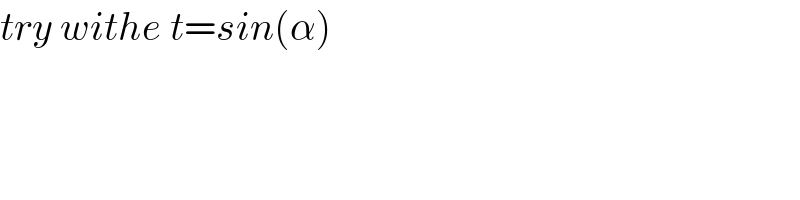
try withe t=sin(α)

$${try}\:{withe}\:{t}={sin}\left(\alpha\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com