Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 81313 by M±th+et£s last updated on 11/Feb/20

∫(((x−2)^3 )/((x+2)^5 )) dx

$$\int\frac{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{3}} }{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{5}} }\:\mathrm{dx} \\ $$

Commented by M±th+et£s last updated on 11/Feb/20

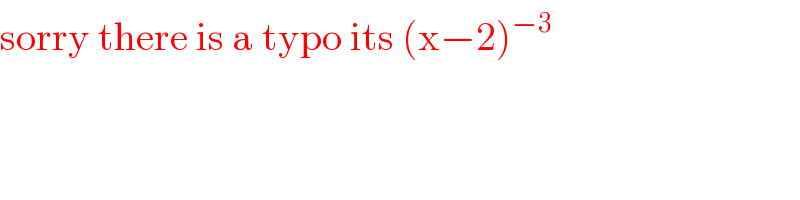
sorry there is a typo its (x−2)^(−3)

$$\mathrm{sorry}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{its}\:\left(\mathrm{x}−\mathrm{2}\right)^{−\mathrm{3}} \:\: \\ $$

Commented by MJS last updated on 11/Feb/20

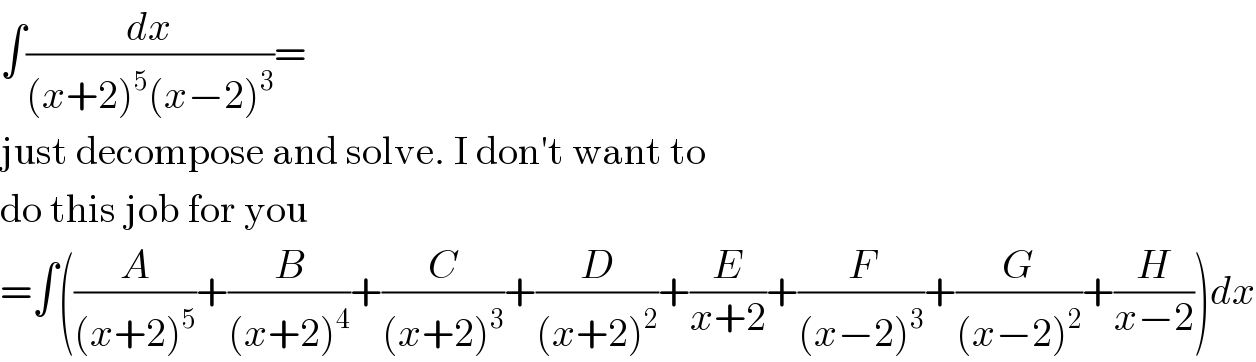
∫(dx/((x+2)^5 (x−2)^3 ))= just decompose and solve. I don′t want to do this job for you =∫((A/((x+2)^5 ))+(B/((x+2)^4 ))+(C/((x+2)^3 ))+(D/((x+2)^2 ))+(E/(x+2))+(F/((x−2)^3 ))+(G/((x−2)^2 ))+(H/(x−2)))dx

$$\int\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{5}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }= \\ $$$$\mathrm{just}\:\mathrm{decompose}\:\mathrm{and}\:\mathrm{solve}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{want}\:\mathrm{to} \\ $$$$\mathrm{do}\:\mathrm{this}\:\mathrm{job}\:\mathrm{for}\:\mathrm{you} \\ $$$$=\int\left(\frac{{A}}{\left({x}+\mathrm{2}\right)^{\mathrm{5}} }+\frac{{B}}{\left({x}+\mathrm{2}\right)^{\mathrm{4}} }+\frac{{C}}{\left({x}+\mathrm{2}\right)^{\mathrm{3}} }+\frac{{D}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{{E}}{{x}+\mathrm{2}}+\frac{{F}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }+\frac{{G}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{{H}}{{x}−\mathrm{2}}\right){dx} \\ $$

Commented by Tony Lin last updated on 12/Feb/20

you can let u=((x+2)/(x−2)) , (du/dx)=((−4)/((x−2)^2 )) x=((2u+2)/(u−1)) ⇒−(1/4) ∫(du/((((4u)/(u−1)))^5 ((4/(u−1))))) =−(1/(4096))∫(((u−1)^6 )/u^5 ) du =−(1/(4096))∫(u+((15)/u)−((20)/u^2 )+((15)/u^3 )−(6/u^4 )+(1/u^5 )−6)du =−(1/(4096))((u^2 /2)+15ln∣u∣+((20)/u)−((15)/(2u^2 ))+(2/u^3 ) −(1/(4u^4 ))−6u)+c plug u=((x+2)/(x−2)) in ⇒∫(dx/((x+2)^5 (x−2)^3 )) =−(1/(4096))[(((((x+2)/(x−2)))^2 )/2)+15ln∣((x+2)/(x−2))∣+((20(x−2))/(x+2)) −((15)/2)(((x−2)/(x+2)))^2 +2(((x−2)/(x+2)))^3 −(1/4)(((x−2)/(x+2)))^4 − ((6(x+2))/(x−2))]+c

$${you}\:{can}\:{let}\:{u}=\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}\:,\:\frac{{du}}{{dx}}=\frac{−\mathrm{4}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${x}=\frac{\mathrm{2}{u}+\mathrm{2}}{{u}−\mathrm{1}} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{4}}\:\int\frac{{du}}{\left(\frac{\mathrm{4}{u}}{{u}−\mathrm{1}}\right)^{\mathrm{5}} \left(\frac{\mathrm{4}}{{u}−\mathrm{1}}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4096}}\int\frac{\left({u}−\mathrm{1}\right)^{\mathrm{6}} }{{u}^{\mathrm{5}} }\:{du}\: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4096}}\int\left({u}+\frac{\mathrm{15}}{{u}}−\frac{\mathrm{20}}{{u}^{\mathrm{2}} }+\frac{\mathrm{15}}{{u}^{\mathrm{3}} }−\frac{\mathrm{6}}{{u}^{\mathrm{4}} }+\frac{\mathrm{1}}{{u}^{\mathrm{5}} }−\mathrm{6}\right){du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4096}}\left(\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{15}{ln}\mid{u}\mid+\frac{\mathrm{20}}{{u}}−\frac{\mathrm{15}}{\mathrm{2}{u}^{\mathrm{2}} }+\frac{\mathrm{2}}{{u}^{\mathrm{3}} }\right. \\ $$$$\left.−\frac{\mathrm{1}}{\mathrm{4}{u}^{\mathrm{4}} }−\mathrm{6}{u}\right)+{c} \\ $$$${plug}\:{u}=\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}\:{in} \\ $$$$\Rightarrow\int\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{5}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }\: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4096}}\left[\frac{\left(\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{15}{ln}\mid\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}\mid+\frac{\mathrm{20}\left({x}−\mathrm{2}\right)}{{x}+\mathrm{2}}\:\:\:\:\:\:\:\:\right. \\ $$$$−\frac{\mathrm{15}}{\mathrm{2}}\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)^{\mathrm{4}} − \\ $$$$\left.\frac{\mathrm{6}\left({x}+\mathrm{2}\right)}{{x}−\mathrm{2}}\right]+{c} \\ $$

Commented by mathmax by abdo last updated on 11/Feb/20

I=∫ (dx/((x−2)^3 (x+2)^5 )) =∫ (dx/((((x−2)/(x+2)))^3 (x+2)^8 )) changement ((x−2)/(x+2)) =t give x−2=xt +2t ⇒(1−t)x=2t +2 ⇒x=((2t+2)/(1−t)) ⇒x+2=2+((2t+2)/(1−t)) =((2−2t+2t+2)/(1−t)) =(4/((1−t))) dx =((2(1−t)−(2t+2)(−1))/((1−t)^2 ))dt =((2−2t+2t+2)/((t−1)^2 )) =(4/((t−1)^2 ))dt ⇒ I=∫ ((4dt)/((t−1)^2 .t^3 ((4/(1−t)))^8 )) =(1/4^7 ) ∫ (((t−1)^8 )/((t−1)^2 .t^3 ))dt =(1/4^7 )∫ (((t−1)^4 )/t^3 )dt=(1/4^7 )∫ ((Σ_(k=0) ^4 C_4 ^k t^k (−1)^(4−k) )/t^3 )dt =(1/4^7 ) ∫ ((C_4 ^0 (−1)^4 −C_4 ^1 t +C_4 ^2 t^2 −C_4 ^3 t^3 +C_4 ^4 t^4 )/t^3 )dt =(1/4^7 )∫ (dt/t^3 )−(C_4 ^1 /4^7 ) ∫ (dt/t^2 ) +(C_4 ^2 /4^7 ) ∫ (dt/t)−(C_4 ^3 /4^7 ) ∫ dt +(1/4^7 ) ∫ tdt =−(1/2)(1/4^7 )×(1/t^2 ) +(1/(4^6 t)) +(C_4 ^2 /4^7 )ln∣t∣−(1/4^6 )t +(1/(2.4^7 ))t^2 +C C_4 ^2 =((4!)/(2!×2!)) =((4×3×2!)/((2!)^2 ))=6 ⇒ I =−(1/(2×4^7 ))(((x+2)/(x−2)))^2 +(1/4^6 )(((x+2)/(x−2))))+(6/4^7 )ln∣((x−2)/(x+2))∣−(1/4^6 )(((x−2)/(x+2)))+(1/(2.4^7 ))(((x−2)/(x+2)))^2 +C

$${I}=\int\:\:\frac{{dx}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{5}} }\:=\int\:\:\:\frac{{dx}}{\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{8}} }\:{changement}\:\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\:={t} \\ $$$${give}\:{x}−\mathrm{2}={xt}\:+\mathrm{2}{t}\:\Rightarrow\left(\mathrm{1}−{t}\right){x}=\mathrm{2}{t}\:+\mathrm{2}\:\Rightarrow{x}=\frac{\mathrm{2}{t}+\mathrm{2}}{\mathrm{1}−{t}}\:\Rightarrow{x}+\mathrm{2}=\mathrm{2}+\frac{\mathrm{2}{t}+\mathrm{2}}{\mathrm{1}−{t}} \\ $$$$=\frac{\mathrm{2}−\mathrm{2}{t}+\mathrm{2}{t}+\mathrm{2}}{\mathrm{1}−{t}}\:=\frac{\mathrm{4}}{\left(\mathrm{1}−{t}\right)} \\ $$$${dx}\:=\frac{\mathrm{2}\left(\mathrm{1}−{t}\right)−\left(\mathrm{2}{t}+\mathrm{2}\right)\left(−\mathrm{1}\right)}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt}\:=\frac{\mathrm{2}−\mathrm{2}{t}+\mathrm{2}{t}+\mathrm{2}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{4}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt}\:\Rightarrow \\ $$$${I}=\int\:\:\frac{\mathrm{4}{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} .{t}^{\mathrm{3}} \left(\frac{\mathrm{4}}{\mathrm{1}−{t}}\right)^{\mathrm{8}} }\:=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\:\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{8}} }{\left({t}−\mathrm{1}\right)^{\mathrm{2}} .{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{4}} }{{t}^{\mathrm{3}} }{dt}=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\int\:\:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \:{t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{4}−{k}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\:\int\:\:\frac{{C}_{\mathrm{4}} ^{\mathrm{0}} \:\left(−\mathrm{1}\right)^{\mathrm{4}} \:−{C}_{\mathrm{4}} ^{\mathrm{1}} \:{t}\:+{C}_{\mathrm{4}} ^{\mathrm{2}} {t}^{\mathrm{2}} −{C}_{\mathrm{4}} ^{\mathrm{3}} \:{t}^{\mathrm{3}} \:+{C}_{\mathrm{4}} ^{\mathrm{4}} \:{t}^{\mathrm{4}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\int\:\frac{{dt}}{{t}^{\mathrm{3}} }−\frac{{C}_{\mathrm{4}} ^{\mathrm{1}} }{\mathrm{4}^{\mathrm{7}} }\:\int\:\frac{{dt}}{{t}^{\mathrm{2}} }\:+\frac{{C}_{\mathrm{4}} ^{\mathrm{2}} }{\mathrm{4}^{\mathrm{7}} }\:\int\:\frac{{dt}}{{t}}−\frac{{C}_{\mathrm{4}} ^{\mathrm{3}} }{\mathrm{4}^{\mathrm{7}} }\:\int\:{dt}\:\:+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\:\int\:{tdt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }×\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:\:+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{6}} {t}}\:+\frac{{C}_{\mathrm{4}} ^{\mathrm{2}} }{\mathrm{4}^{\mathrm{7}} }{ln}\mid{t}\mid−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{6}} }{t}\:\:+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}^{\mathrm{7}} }{t}^{\mathrm{2}} \:+{C} \\ $$$${C}_{\mathrm{4}} ^{\mathrm{2}} \:=\frac{\mathrm{4}!}{\mathrm{2}!×\mathrm{2}!}\:=\frac{\mathrm{4}×\mathrm{3}×\mathrm{2}!}{\left(\mathrm{2}!\right)^{\mathrm{2}} }=\mathrm{6}\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}×\mathrm{4}^{\mathrm{7}} }\left(\frac{{x}+\mathrm{2}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{6}} }\left(\frac{{x}+\mathrm{2}}{\left.{x}−\mathrm{2}\right)}\right)+\frac{\mathrm{6}}{\mathrm{4}^{\mathrm{7}} }{ln}\mid\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\mid−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{6}} }\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}^{\mathrm{7}} }\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} \:+{C} \\ $$

Commented by msup trace by abdo last updated on 12/Feb/20

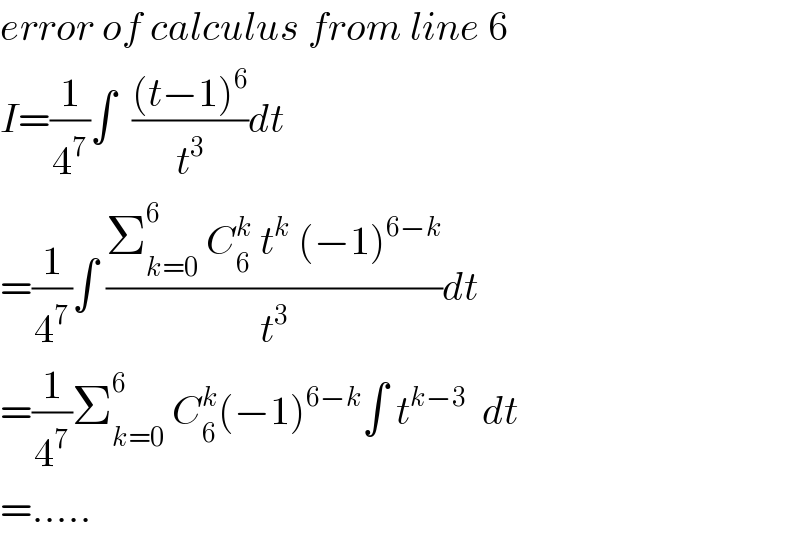
error of calculus from line 6 I=(1/4^7 )∫ (((t−1)^6 )/t^3 )dt =(1/4^7 )∫ ((Σ_(k=0) ^6 C_6 ^k t^k (−1)^(6−k) )/t^3 )dt =(1/4^7 )Σ_(k=0) ^6 C_6 ^k (−1)^(6−k) ∫ t^(k−3) dt =.....

$${error}\:{of}\:{calculus}\:{from}\:{line}\:\mathrm{6} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{6}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\int\:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{6}} \:{C}_{\mathrm{6}} ^{{k}} \:{t}^{{k}} \:\left(−\mathrm{1}\right)^{\mathrm{6}−{k}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{7}} }\sum_{{k}=\mathrm{0}} ^{\mathrm{6}} \:{C}_{\mathrm{6}} ^{{k}} \left(−\mathrm{1}\right)^{\mathrm{6}−{k}} \int\:{t}^{{k}−\mathrm{3}} \:\:{dt} \\ $$$$=..... \\ $$

Answered by MJS last updated on 12/Feb/20

∫(dx/((x+2)^5 (x−2)^3 ))=? Ostrogradski′s Method ∫((P(x))/(Q(x)))dx=((P_1 (x))/(Q_1 (x)))+∫((P_2 (x))/(Q_2 (x)))dx Q_1 (x)=gcd (Q(x), Q′(x)) =(x+2)^4 (x−2)^2 Q_2 (x)=((Q(x))/(Q_1 (x)))=(x+2)(x−2) ((P(x))/(Q(x)))=(d/dx)[((P_1 (x))/(Q_1 (x)))]+((P_2 (x))/(Q_2 (x))) (1/((x+2)^5 (x−2)^3 ))=(d/dx)[((ax^5 +bx^4 +cx^3 +dx^2 +ex+f)/((x+2)^4 (x−2)^2 ))]+((gx+h)/((x+2)(x−2))) ⇒ P_1 (x)=((15)/(4096))x^5 +((15)/(1024))x^4 −(5/(512))x^3 −((25)/(256))x^2 −((17)/(256))x+(1/8) P_2 (x)=((15)/(4096)) ∫(dx/((x+2)^5 (x−2)^3 ))= =((15x^5 +60x^4 −40x^3 −400x^2 −272x+512)/(4096(x+2)^4 (x−2)^2 ))+((15)/(4096))∫(dx/((x+2)(x−2)))= =((15x^5 +60x^4 −40x^3 −400x^2 −272x+512)/(4096(x+2)^4 (x−2)^2 ))+((15)/(16384))ln ∣((x−2)/(x+2))∣ +C

$$\int\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{5}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }=? \\ $$$$\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method} \\ $$$$\int\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}{dx}=\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)}{dx} \\ $$$${Q}_{\mathrm{1}} \left({x}\right)=\mathrm{gcd}\:\left({Q}\left({x}\right),\:{Q}'\left({x}\right)\right)\:=\left({x}+\mathrm{2}\right)^{\mathrm{4}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$${Q}_{\mathrm{2}} \left({x}\right)=\frac{{Q}\left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}=\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right) \\ $$$$\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}=\frac{{d}}{{dx}}\left[\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}\right]+\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)} \\ $$$$\frac{\mathrm{1}}{\left({x}+\mathrm{2}\right)^{\mathrm{5}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }=\frac{{d}}{{dx}}\left[\frac{{ax}^{\mathrm{5}} +{bx}^{\mathrm{4}} +{cx}^{\mathrm{3}} +{dx}^{\mathrm{2}} +{ex}+{f}}{\left({x}+\mathrm{2}\right)^{\mathrm{4}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} }\right]+\frac{{gx}+{h}}{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)} \\ $$$$\Rightarrow \\ $$$${P}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{15}}{\mathrm{4096}}{x}^{\mathrm{5}} +\frac{\mathrm{15}}{\mathrm{1024}}{x}^{\mathrm{4}} −\frac{\mathrm{5}}{\mathrm{512}}{x}^{\mathrm{3}} −\frac{\mathrm{25}}{\mathrm{256}}{x}^{\mathrm{2}} −\frac{\mathrm{17}}{\mathrm{256}}{x}+\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${P}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{15}}{\mathrm{4096}} \\ $$$$\int\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{5}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }= \\ $$$$=\frac{\mathrm{15}{x}^{\mathrm{5}} +\mathrm{60}{x}^{\mathrm{4}} −\mathrm{40}{x}^{\mathrm{3}} −\mathrm{400}{x}^{\mathrm{2}} −\mathrm{272}{x}+\mathrm{512}}{\mathrm{4096}\left({x}+\mathrm{2}\right)^{\mathrm{4}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{15}}{\mathrm{4096}}\int\frac{{dx}}{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)}= \\ $$$$=\frac{\mathrm{15}{x}^{\mathrm{5}} +\mathrm{60}{x}^{\mathrm{4}} −\mathrm{40}{x}^{\mathrm{3}} −\mathrm{400}{x}^{\mathrm{2}} −\mathrm{272}{x}+\mathrm{512}}{\mathrm{4096}\left({x}+\mathrm{2}\right)^{\mathrm{4}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{15}}{\mathrm{16384}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\mid\:+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com