Question Number 81336 by mathmax by abdo last updated on 11/Feb/20
$${decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{3}\right)^{\mathrm{7}} } \\ $$$${and}\:{detrmine}\:\:\int\:{F}\left({x}\right){dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{2}} ^{+\infty} \:{F}\left({x}\right){dx} \\ $$
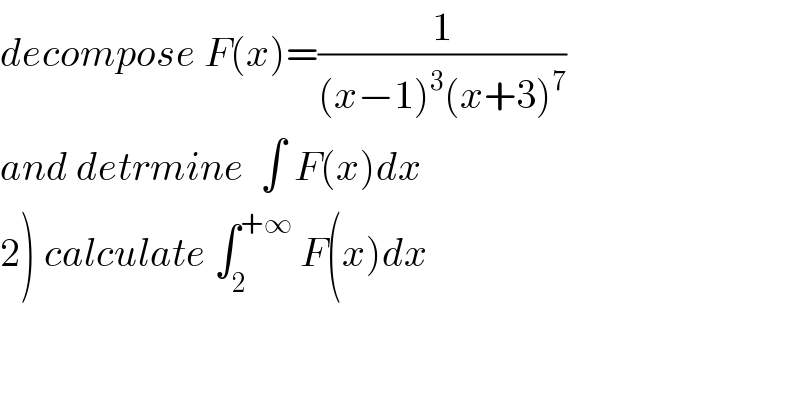
Commented by Tony Lin last updated on 12/Feb/20
![∫(dx/((x−1)^3 (x+3)^7 )) let u=((x+3)/(x−1)) , (du/dx)=((−4)/((x−1)^2 )) x=((u+3)/(u−1)) ⇒−(1/4)∫(du/(((4/(u−1)))(((4u)/(u−1)))^7 )) =−(1/4^9 )∫(((u−1)^8 )/u^7 )du =∫(u−8+((28)/u)−((56)/u^2 )+((70)/u^3 )−((56)/u^4 )+((28)/u^5 )−(8/u^6 )+(1/u^7 ))du ×(−(1/4^9 )) =((u^2 /2)−8u+28ln∣u∣+((56)/u)−((35)/u^2 )+((56)/(3u^3 ))−(7/u^4 ) +(8/(5u^5 ))−(1/(6u^(6 ) )))×(−(1/(262144)))+c plug u=((x+3)/(x−1)) in ⇒∫(dx/((x−1)^3 (x+3)^7 )) =−(1/(262144))[(((((x+3)/(x−1)))^2 )/2)−((8(x+3))/(x−1))+28ln∣((x+3)/(x−1))∣ +((56(x−1))/(x+3))−35(((x−1)/(x+3)))^2 +((56)/3)(((x−1)/(x+3)))^3 − 7(((x−1)/(x+3)))^4 +(8/5)(((x−1)/(x+3)))^5 −(1/6)(((x−1)/(x+3)))^6 ]+c](Q81361.png)
$$\int\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{3}\right)^{\mathrm{7}} } \\ $$$${let}\:{u}=\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\:,\:\frac{{du}}{{dx}}=\frac{−\mathrm{4}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${x}=\frac{{u}+\mathrm{3}}{{u}−\mathrm{1}} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{du}}{\left(\frac{\mathrm{4}}{{u}−\mathrm{1}}\right)\left(\frac{\mathrm{4}{u}}{{u}−\mathrm{1}}\right)^{\mathrm{7}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\int\frac{\left({u}−\mathrm{1}\right)^{\mathrm{8}} }{{u}^{\mathrm{7}} }{du} \\ $$$$=\int\left({u}−\mathrm{8}+\frac{\mathrm{28}}{{u}}−\frac{\mathrm{56}}{{u}^{\mathrm{2}} }+\frac{\mathrm{70}}{{u}^{\mathrm{3}} }−\frac{\mathrm{56}}{{u}^{\mathrm{4}} }+\frac{\mathrm{28}}{{u}^{\mathrm{5}} }−\frac{\mathrm{8}}{{u}^{\mathrm{6}} }+\frac{\mathrm{1}}{{u}^{\mathrm{7}} }\right){du} \\ $$$$×\left(−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\right) \\ $$$$=\left(\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{8}{u}+\mathrm{28}{ln}\mid{u}\mid+\frac{\mathrm{56}}{{u}}−\frac{\mathrm{35}}{{u}^{\mathrm{2}} }+\frac{\mathrm{56}}{\mathrm{3}{u}^{\mathrm{3}} }−\frac{\mathrm{7}}{{u}^{\mathrm{4}} }\right. \\ $$$$\left.+\frac{\mathrm{8}}{\mathrm{5}{u}^{\mathrm{5}} }−\frac{\mathrm{1}}{\mathrm{6}{u}^{\mathrm{6}\:} }\right)×\left(−\frac{\mathrm{1}}{\mathrm{262144}}\right)+{c} \\ $$$${plug}\:{u}=\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\:{in} \\ $$$$\Rightarrow\int\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{3}\right)^{\mathrm{7}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{262144}}\left[\frac{\left(\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{8}\left({x}+\mathrm{3}\right)}{{x}−\mathrm{1}}+\mathrm{28}{ln}\mid\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\mid\right. \\ $$$$+\frac{\mathrm{56}\left({x}−\mathrm{1}\right)}{{x}+\mathrm{3}}−\mathrm{35}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{56}}{\mathrm{3}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{3}} − \\ $$$$\left.\mathrm{7}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{4}} +\frac{\mathrm{8}}{\mathrm{5}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{5}} −\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{6}} \right]+{c} \\ $$
Commented by Tony Lin last updated on 12/Feb/20
![∫(dx/((x+a)^m (x+b)^n )) let u=((x+b)/(x+a)) , (du/dx)=((a−b)/((x+a)^2 )) x=((b−au)/(u−1)) ⇒(1/(a−b))∫(du/((((b−a)/(u−1)))^(m−2) [(((b−a)u)/(u−1))]^n )) =−(1/((b−a)^(m+n−1) ))∫ (((u−1)^(m+n−2) )/u^n )du =∫((Σ_(r=0) ^(m+n−2) C_r ^(m+n−2) (((x+b)/(x+a)))^(r−n) (−1)^(m+n−2−r) )/(−(b−a)^(m+n−1) ))d(((x+b)/(x+a)))](Q81363.png)
$$\int\frac{{dx}}{\left({x}+{a}\right)^{{m}} \left({x}+{b}\right)^{{n}} } \\ $$$${let}\:{u}=\frac{{x}+{b}}{{x}+{a}}\:,\:\frac{{du}}{{dx}}=\frac{{a}−{b}}{\left({x}+{a}\right)^{\mathrm{2}} } \\ $$$${x}=\frac{{b}−{au}}{{u}−\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}−{b}}\int\frac{{du}}{\left(\frac{{b}−{a}}{{u}−\mathrm{1}}\right)^{{m}−\mathrm{2}} \left[\frac{\left({b}−{a}\right){u}}{{u}−\mathrm{1}}\right]^{{n}} } \\ $$$$=−\frac{\mathrm{1}}{\left({b}−{a}\right)^{{m}+{n}−\mathrm{1}} }\int\:\frac{\left({u}−\mathrm{1}\right)^{{m}+{n}−\mathrm{2}} }{{u}^{{n}} }{du} \\ $$$$=\int\frac{\underset{{r}=\mathrm{0}} {\overset{{m}+{n}−\mathrm{2}} {\sum}}{C}_{{r}} ^{{m}+{n}−\mathrm{2}} \left(\frac{{x}+{b}}{{x}+{a}}\right)^{{r}−{n}} \left(−\mathrm{1}\right)^{{m}+{n}−\mathrm{2}−{r}} }{−\left({b}−{a}\right)^{{m}+{n}−\mathrm{1}} }{d}\left(\frac{{x}+{b}}{{x}+{a}}\right) \\ $$
Commented by mathmax by abdo last updated on 12/Feb/20
$${thank}\:{you}\:{sir}. \\ $$
Commented by MJS last updated on 12/Feb/20
$$\mathrm{on}\:\mathrm{my}\:\mathrm{path}\:\mathrm{the}\:\mathrm{hard}\:\mathrm{work}\:\mathrm{is}\:\mathrm{solving}\:\mathrm{the} \\ $$$$\mathrm{system}\:\mathrm{for}\:\mathrm{the}\:\mathrm{coefficients}\:{c}_{{j}} \\ $$$$\mathrm{on}\:\mathrm{your}\:\mathrm{path}\:\mathrm{it}\:\mathrm{is}\:\mathrm{to}\:\mathrm{compose}\:\mathrm{all}\:\mathrm{those}\:\mathrm{fractions} \\ $$$$\mathrm{if}\:\mathrm{needed} \\ $$
Commented by mathmax by abdo last updated on 12/Feb/20
$$\int{F}\left({x}\right){dx}\:=\int\:\:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{3}\right)^{\mathrm{7}} }\:=\int\:\:\frac{{dx}}{\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{3}} \left({x}+\mathrm{3}\right)^{\mathrm{10}} }\:{changement} \\ $$$$\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}={t}\:{give}\:{x}−\mathrm{1}={tx}+\mathrm{3}{t}\:\Rightarrow\left(\mathrm{1}−{t}\right){x}=\mathrm{3}{t}+\mathrm{1}\:\Rightarrow{x}=\frac{\mathrm{3}{t}+\mathrm{1}}{\mathrm{1}−{t}}\:\Rightarrow \\ $$$${x}+\mathrm{3}=\mathrm{3}+\frac{\mathrm{3}{t}+\mathrm{1}}{\mathrm{1}−{t}}\:=\frac{\mathrm{3}−\mathrm{3}{t}+\mathrm{3}{t}+\mathrm{1}}{\mathrm{1}−{t}}\:=\frac{\mathrm{4}}{\mathrm{1}−{t}}\:\Rightarrow{dx}\:=\frac{\mathrm{4}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int{F}\left({x}\right){dx}\:=\int\:\frac{\mathrm{4}{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{3}} \left(\frac{\mathrm{4}}{\mathrm{1}−{t}}\right)^{\mathrm{10}} }\:=\mathrm{4}\:\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{10}} }{\mathrm{4}^{\mathrm{10}} \left({t}−\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\:\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{8}} }{{t}^{\mathrm{3}} }{dt}\:=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\int\:\:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{8}} \:{C}_{\mathrm{8}} ^{{k}} \:{t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{8}−{k}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\:\int\:\:\frac{\mathrm{1}−{C}_{\mathrm{8}} ^{\mathrm{1}} \:{t}\:+{C}_{\mathrm{8}} ^{\mathrm{2}} \:{t}^{\mathrm{2}} −{C}_{\mathrm{8}} ^{\mathrm{3}} \:{t}^{\mathrm{3}} \:+{C}_{\mathrm{8}} ^{\mathrm{4}} \:{t}^{\mathrm{4}} −{C}_{\mathrm{8}} ^{\mathrm{5}} \:{t}^{\mathrm{5}} \:+{C}_{\mathrm{8}} ^{\mathrm{6}} \:{t}^{\mathrm{6}} −{C}_{\mathrm{8}} ^{\mathrm{7}} {t}^{\mathrm{7}} +{C}_{\mathrm{8}} ^{\mathrm{8}} \:{t}^{\mathrm{8}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\:\int\:\frac{{dt}}{{t}^{\mathrm{3}} }\:−\frac{{C}_{\mathrm{8}} ^{\mathrm{1}} }{\mathrm{4}^{\mathrm{9}} }\:\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} }\:+\frac{{C}_{\mathrm{8}} ^{\mathrm{2}} }{\mathrm{4}^{\mathrm{9}} }\int\:\frac{{dt}}{{t}}\:−\frac{{C}_{\mathrm{8}} ^{\mathrm{3}} }{\mathrm{4}^{\mathrm{9}} }\int{dt}\:\:\frac{{C}_{\mathrm{8}} ^{\mathrm{4}} }{\mathrm{4}^{\mathrm{9}} }\:\int\:{tdt}−\frac{{C}_{\mathrm{8}} ^{\mathrm{5}} }{\mathrm{4}^{\mathrm{9}} }\:\int\:{t}^{\mathrm{2}} {dt} \\ $$$$+\frac{{C}_{\mathrm{8}} ^{\mathrm{6}} }{\mathrm{4}^{\mathrm{9}} }\int\:{t}^{\mathrm{3}} \:{dt}\:−\frac{{C}_{\mathrm{8}} ^{\mathrm{7}} }{\mathrm{4}^{\mathrm{9}} }\:\int\:{t}^{\mathrm{4}} \:{dt}\:\:+\frac{{C}_{\mathrm{8}} ^{\mathrm{8}} }{\mathrm{4}^{\mathrm{9}} }\int\:{t}^{\mathrm{5}} \:{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}×\mathrm{4}^{\mathrm{9}} \:×{t}^{\mathrm{2}} }\:+\frac{\mathrm{8}}{\mathrm{4}^{\mathrm{9}} ×{t}}\:+\frac{{C}_{\mathrm{8}} ^{\mathrm{2}} }{\mathrm{4}^{\mathrm{9}} }{ln}\mid{t}\mid−\frac{{C}_{\mathrm{8}} ^{\mathrm{3}} }{\mathrm{4}^{\mathrm{9}} }{t}\:\:+\frac{{C}_{\mathrm{8}} ^{\mathrm{4}} }{\mathrm{2}.\mathrm{4}^{\mathrm{9}} }{t}^{\mathrm{2}} −\frac{{C}_{\mathrm{8}} ^{\mathrm{5}} }{\mathrm{3}.\mathrm{4}^{\mathrm{9}} }{t}^{\mathrm{3}} \:+\frac{{C}_{\mathrm{8}} ^{\mathrm{6}} }{\mathrm{4}^{\mathrm{10}} }{t}^{\mathrm{4}} \\ $$$$−\frac{{C}_{\mathrm{8}} ^{\mathrm{7}} }{\mathrm{5}.\mathrm{4}^{\mathrm{9}} }{t}^{\mathrm{5}} \:+\frac{\mathrm{1}}{\mathrm{6}.\mathrm{4}^{\mathrm{9}} }{t}^{\mathrm{6}} \:+{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}^{\mathrm{9}} }\left(\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} \:+\frac{\mathrm{8}}{\mathrm{4}^{\mathrm{9}} }\left(\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\right)+\frac{{C}_{\mathrm{8}} ^{\mathrm{2}} }{\mathrm{4}^{\mathrm{9}} }{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\mid−\frac{{C}_{\mathrm{8}} ^{\mathrm{3}} }{\mathrm{4}^{\mathrm{9}} }\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right) \\ $$$$+\frac{{C}_{\mathrm{8}} ^{\mathrm{4}} }{\mathrm{2}.\mathrm{4}^{\mathrm{9}} }\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{2}} \:−\frac{{C}_{\mathrm{8}} ^{\mathrm{5}} }{\mathrm{3}.\mathrm{4}^{\mathrm{9}} }\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{3}} \:+\frac{{C}_{\mathrm{8}} ^{\mathrm{6}} }{\mathrm{4}^{\mathrm{10}} }\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{4}} \:−\frac{{C}_{\mathrm{8}} ^{\mathrm{7}} }{\mathrm{5}.\mathrm{4}^{\mathrm{9}} }\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{5}} \:+\frac{\mathrm{1}}{\mathrm{6}.\mathrm{4}^{\mathrm{9}} }\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{6}} \:+{C} \\ $$$$ \\ $$
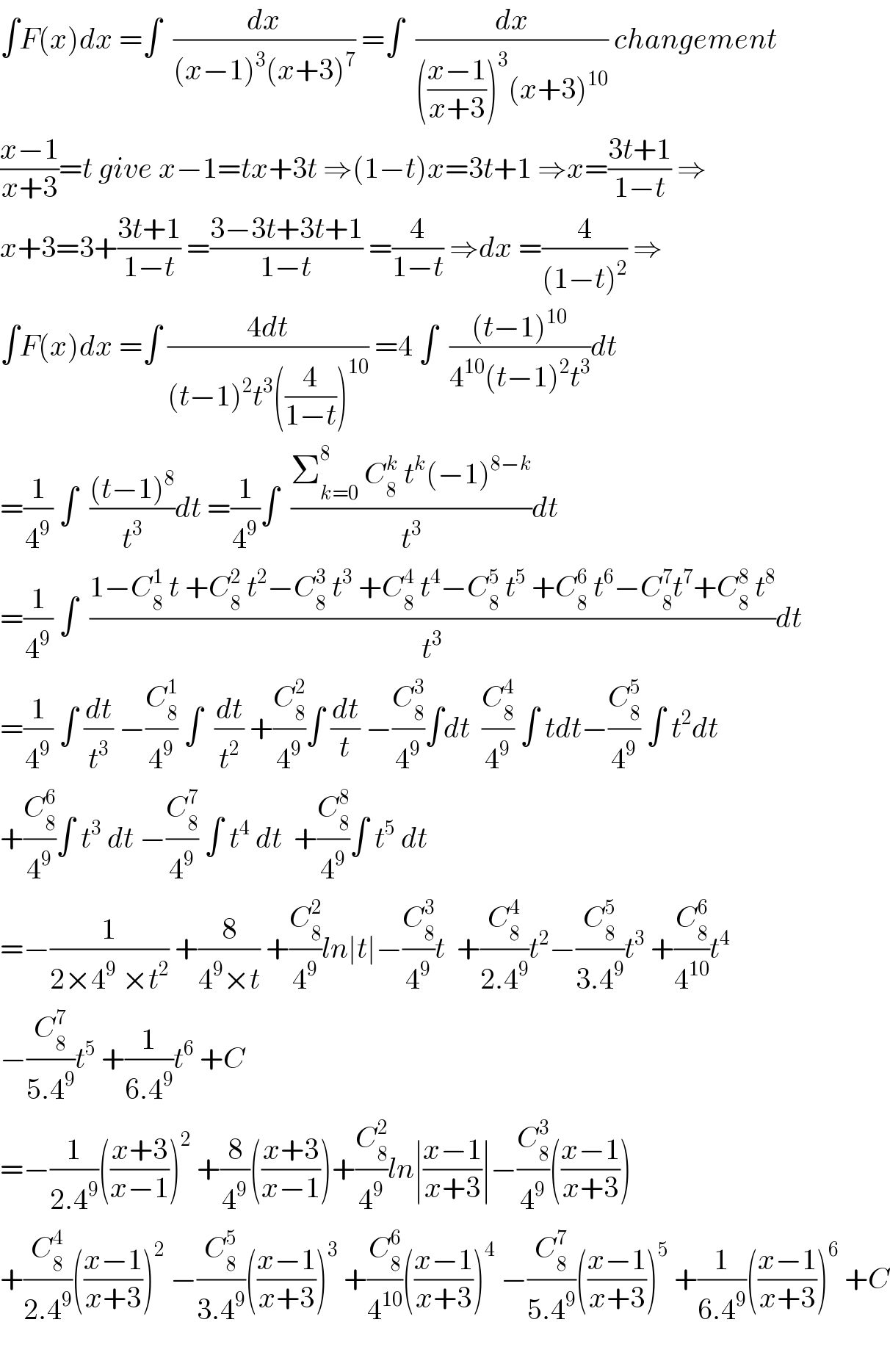
Commented by mathmax by abdo last updated on 12/Feb/20
![∫_2 ^(+∞) F(x)dx =−(1/(2.4^9 ))[(((x+3)/(x−1)))^2 ]_2 ^(+∞) +(8/4^9 )[(((x+3)/(x−1)))]_2 ^(+∞) +(C_8 ^2 /4^9 )[ln∣((x−1)/(x+3))∣]_2 ^(+∞) −(C_8 ^3 /4^9 )[(((x−1)/(x+3)))]_2 ^(+∞) +(C_8 ^4 /(2.4^9 ))[(((x−1)/(x+3)))^2 ]_2 ^(+∞) −(C_8 ^5 /(3.4^9 ))[(((x−1)/(x+3)))^3 ]_2 ^(+∞) +(C_8 ^6 /4^(10) )[(((x−1)/(x+3)))^4 ]_2 ^(+∞) −(C_8 ^7 /(5.4^9 ))[(((x−1)/(x+3)))^5 ]_2 ^(+∞) +(1/(6.4^9 ))[(((x−1)/(x+3)))^6 ]_2 ^(+∞) =−(1/(2.4^9 )){1−5^2 }+(8/4^9 ){1−5}+(C_8 ^2 /4^9 ){−ln((1/5))} −(C_8 ^3 /4^9 ){1−(1/5)}+(C_8 ^4 /(2.4^9 )){1−((1/5))^2 }−(C_8 ^5 /(3.4^9 )){1−((1/5))^3 } +(C_8 ^6 /4^(10) ){1−((1/5))^4 }−(C_8 ^7 /(5.4^9 )){1−((1/5))^5 } +(1/(6.4^9 )){1−((1/5))^6 }](Q81378.png)
$$\int_{\mathrm{2}} ^{+\infty} {F}\left({x}\right){dx}\:=−\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}^{\mathrm{9}} }\left[\left(\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} \right]_{\mathrm{2}} ^{+\infty} \:+\frac{\mathrm{8}}{\mathrm{4}^{\mathrm{9}} }\left[\left(\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\right)\right]_{\mathrm{2}} ^{+\infty} \:+\frac{{C}_{\mathrm{8}} ^{\mathrm{2}} }{\mathrm{4}^{\mathrm{9}} }\left[{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\mid\right]_{\mathrm{2}} ^{+\infty} \\ $$$$−\frac{{C}_{\mathrm{8}} ^{\mathrm{3}} }{\mathrm{4}^{\mathrm{9}} }\left[\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)\right]_{\mathrm{2}} ^{+\infty} \:+\frac{{C}_{\mathrm{8}} ^{\mathrm{4}} }{\mathrm{2}.\mathrm{4}^{\mathrm{9}} }\left[\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{2}} \right]_{\mathrm{2}} ^{+\infty} −\frac{{C}_{\mathrm{8}} ^{\mathrm{5}} }{\mathrm{3}.\mathrm{4}^{\mathrm{9}} }\left[\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{3}} \right]_{\mathrm{2}} ^{+\infty} \\ $$$$+\frac{{C}_{\mathrm{8}} ^{\mathrm{6}} }{\mathrm{4}^{\mathrm{10}} }\left[\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{4}} \right]_{\mathrm{2}} ^{+\infty} −\frac{{C}_{\mathrm{8}} ^{\mathrm{7}} }{\mathrm{5}.\mathrm{4}^{\mathrm{9}} }\left[\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{5}} \right]_{\mathrm{2}} ^{+\infty} +\frac{\mathrm{1}}{\mathrm{6}.\mathrm{4}^{\mathrm{9}} }\left[\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\right)^{\mathrm{6}} \right]_{\mathrm{2}} ^{+\infty} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}^{\mathrm{9}} }\left\{\mathrm{1}−\mathrm{5}^{\mathrm{2}} \right\}+\frac{\mathrm{8}}{\mathrm{4}^{\mathrm{9}} }\left\{\mathrm{1}−\mathrm{5}\right\}+\frac{{C}_{\mathrm{8}} ^{\mathrm{2}} }{\mathrm{4}^{\mathrm{9}} }\left\{−{ln}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\right\} \\ $$$$−\frac{{C}_{\mathrm{8}} ^{\mathrm{3}} }{\mathrm{4}^{\mathrm{9}} }\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\right\}+\frac{{C}_{\mathrm{8}} ^{\mathrm{4}} }{\mathrm{2}.\mathrm{4}^{\mathrm{9}} }\left\{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} \right\}−\frac{{C}_{\mathrm{8}} ^{\mathrm{5}} }{\mathrm{3}.\mathrm{4}^{\mathrm{9}} }\left\{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{3}} \right\} \\ $$$$+\frac{{C}_{\mathrm{8}} ^{\mathrm{6}} }{\mathrm{4}^{\mathrm{10}} }\left\{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{4}} \right\}−\frac{{C}_{\mathrm{8}} ^{\mathrm{7}} }{\mathrm{5}.\mathrm{4}^{\mathrm{9}} }\left\{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{5}} \right\}\:+\frac{\mathrm{1}}{\mathrm{6}.\mathrm{4}^{\mathrm{9}} }\left\{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{6}} \right\} \\ $$
Commented by mathmax by abdo last updated on 12/Feb/20
$${the}\:{avantage}\:{of}\:{this}\:{method}\:{is}\:{finding}\:{integral}\:{without}\:{passing} \\ $$$${by}\:{decomposition}..! \\ $$
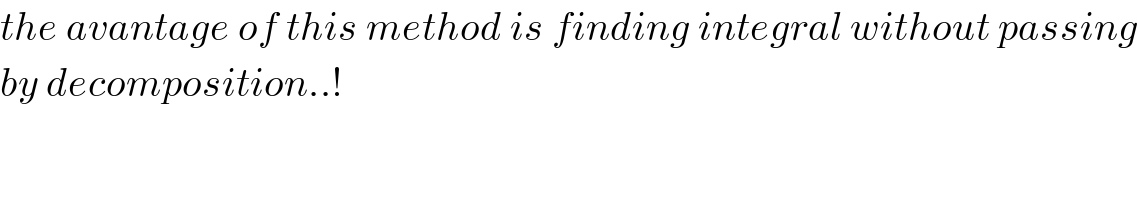
Answered by MJS last updated on 12/Feb/20
![Ostrogradski′s Method again (it′s faster in my opinion) ∫(dx/((x+3)^7 (x−1)^3 )) ∫((P(x))/(Q(x)))dx=((P_1 (x))/(Q_1 (x)))+∫((P_2 (x))/(Q_2 (x)))dx Q_1 (x)=gcd (Q(x), Q^′ (x))=(x+3)^6 (x−1)^2 oo Q_2 (x)=((Q(x))/(Q_1 (x)))=(x+3)(x−1) ((P(x))/(Q(x)))=(d/dx)[((P_1 (x))/(Q_1 (x)))]+((P_2 (x))/(Q_2 (x))) (1/((x+3)^7 (x−1)^3 ))=(d/dx)[((Σ_(j=0) ^7 c_j x^j )/((x+3)^6 (x−1)^2 ))]+((d_1 x+d_0 )/((x+3)(x−1))) ⇒ P_1 (x)=((105x^7 +1575x^6 +9065x^5 +23135x^4 +15491x^3 −38339x^2 −56405x+14653)/(245760)) P_2 (x)=(7/(16384)) ⇒ we only have to solve (7/(16384))∫(dx/((x+3)(x−1)))= =(7/(65536))ln ∣((x−1)/(x+3))∣ ∫(dx/((x+3)^7 (x−1)^3 ))= =((105x^7 +1575x^6 +9065x^5 +23135x^4 +15491x^3 −38339x^2 −56405x+14653)/(245760(x+3)^6 (x−1)^2 ))+(7/(65536))ln ∣((x−1)/(x+3))∣ +C ∫_2 ^∞ (dx/((x+3)^7 (x−1)^3 ))=((−517516+328125ln 5)/(3072000000))](Q81344.png)
$$\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\:\mathrm{again}\:\left(\mathrm{it}'\mathrm{s}\:\mathrm{faster}\:\mathrm{in}\:\mathrm{my}\right. \\ $$$$\left.\mathrm{opinion}\right) \\ $$$$\int\frac{{dx}}{\left({x}+\mathrm{3}\right)^{\mathrm{7}} \left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\int\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}{dx}=\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)}{dx} \\ $$$${Q}_{\mathrm{1}} \left({x}\right)=\mathrm{gcd}\:\left({Q}\left({x}\right),\:{Q}^{'} \left({x}\right)\right)=\left({x}+\mathrm{3}\right)^{\mathrm{6}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} {oo} \\ $$$${Q}_{\mathrm{2}} \left({x}\right)=\frac{{Q}\left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}=\left({x}+\mathrm{3}\right)\left({x}−\mathrm{1}\right) \\ $$$$\frac{{P}\left({x}\right)}{{Q}\left({x}\right)}=\frac{{d}}{{dx}}\left[\frac{{P}_{\mathrm{1}} \left({x}\right)}{{Q}_{\mathrm{1}} \left({x}\right)}\right]+\frac{{P}_{\mathrm{2}} \left({x}\right)}{{Q}_{\mathrm{2}} \left({x}\right)} \\ $$$$\frac{\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{7}} \left({x}−\mathrm{1}\right)^{\mathrm{3}} }=\frac{{d}}{{dx}}\left[\frac{\underset{{j}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}{c}_{{j}} {x}^{{j}} }{\left({x}+\mathrm{3}\right)^{\mathrm{6}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right]+\frac{{d}_{\mathrm{1}} {x}+{d}_{\mathrm{0}} }{\left({x}+\mathrm{3}\right)\left({x}−\mathrm{1}\right)} \\ $$$$\Rightarrow \\ $$$${P}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{105}{x}^{\mathrm{7}} +\mathrm{1575}{x}^{\mathrm{6}} +\mathrm{9065}{x}^{\mathrm{5}} +\mathrm{23135}{x}^{\mathrm{4}} +\mathrm{15491}{x}^{\mathrm{3}} −\mathrm{38339}{x}^{\mathrm{2}} −\mathrm{56405}{x}+\mathrm{14653}}{\mathrm{245760}} \\ $$$${P}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{7}}{\mathrm{16384}} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{only}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\frac{\mathrm{7}}{\mathrm{16384}}\int\frac{{dx}}{\left({x}+\mathrm{3}\right)\left({x}−\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{7}}{\mathrm{65536}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\mid \\ $$$$\int\frac{{dx}}{\left({x}+\mathrm{3}\right)^{\mathrm{7}} \left({x}−\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$=\frac{\mathrm{105}{x}^{\mathrm{7}} +\mathrm{1575}{x}^{\mathrm{6}} +\mathrm{9065}{x}^{\mathrm{5}} +\mathrm{23135}{x}^{\mathrm{4}} +\mathrm{15491}{x}^{\mathrm{3}} −\mathrm{38339}{x}^{\mathrm{2}} −\mathrm{56405}{x}+\mathrm{14653}}{\mathrm{245760}\left({x}+\mathrm{3}\right)^{\mathrm{6}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{7}}{\mathrm{65536}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}\mid\:+{C} \\ $$$$\underset{\mathrm{2}} {\overset{\infty} {\int}}\frac{{dx}}{\left({x}+\mathrm{3}\right)^{\mathrm{7}} \left({x}−\mathrm{1}\right)^{\mathrm{3}} }=\frac{−\mathrm{517516}+\mathrm{328125ln}\:\mathrm{5}}{\mathrm{3072000000}} \\ $$
Commented by john santu last updated on 12/Feb/20
$${ostrogradski}'{s}\:{method}\:{can}\:{use}\:{any}\: \\ $$$${type}\:{integral}? \\ $$
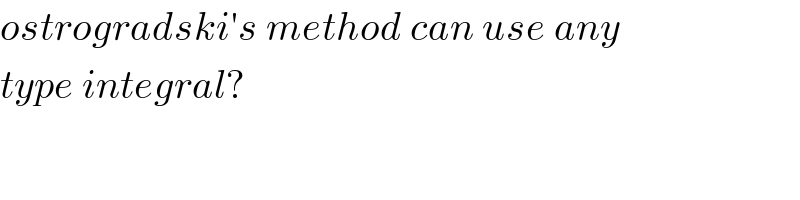
Commented by msup trace by abdo last updated on 12/Feb/20
$${thank}\:{you}\:{sir}\:. \\ $$
Commented by MJS last updated on 12/Feb/20
$$\mathrm{no}.\:{P}\left({x}\right)\:\mathrm{and}\:{Q}\left({x}\right)\:\mathrm{must}\:\mathrm{be}\:\mathrm{polynomes}. \\ $$$$\mathrm{the}\:\mathrm{degree}\:\mathrm{of}\:{P}\left({x}\right)\:\mathrm{must}\:\mathrm{be}\:\mathrm{smaller}\:\mathrm{than} \\ $$$$\mathrm{the}\:\mathrm{degree}\:\mathrm{of}\:{Q}\left({x}\right)\:\mathrm{and}\:\mathrm{all}\:\mathrm{coefficients}\:\mathrm{must} \\ $$$$\mathrm{be}\:\mathrm{real} \\ $$$$\mathrm{the}\:\mathrm{degree}\:\mathrm{of}\:{P}_{\mathrm{1}} \left({x}\right)\:\mathrm{will}\:\mathrm{then}\:\mathrm{be}\:\mathrm{smaller}\:\mathrm{than} \\ $$$$\mathrm{the}\:\mathrm{degree}\:\mathrm{of}\:{Q}_{\mathrm{1}} \left({x}\right),\:\mathrm{same}\:\mathrm{for}\:{P}_{\mathrm{2}} \left({x}\right)\:\mathrm{and}\:{Q}_{\mathrm{2}} \left({x}\right) \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{can}\:\mathrm{find}\:\mathrm{information}\:\mathrm{on}\:\mathrm{wikipedia} \\ $$
Commented by jagoll last updated on 12/Feb/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{mister} \\ $$