Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 8155 by 314159 last updated on 02/Oct/16

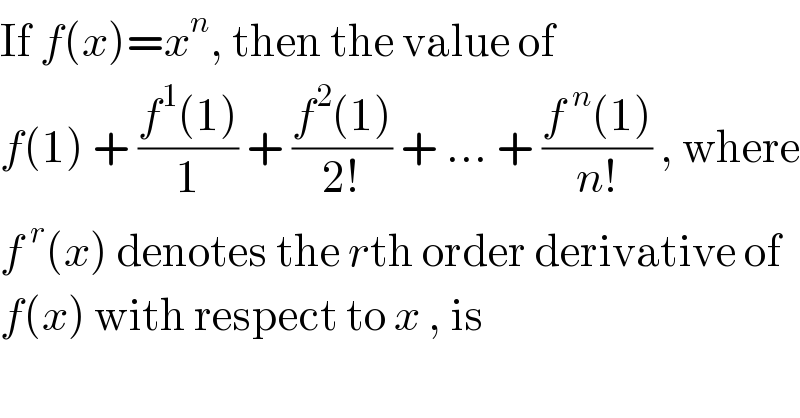
If f(x)=x^n , then the value of f(1) + ((f^1 (1))/1) + ((f^2 (1))/(2!)) + ... + ((f^( n) (1))/(n!)) , where f^( r) (x) denotes the rth order derivative of f(x) with respect to x , is

$$\mathrm{If}\:{f}\left({x}\right)={x}^{{n}} ,\:\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$${f}\left(\mathrm{1}\right)\:+\:\frac{{f}^{\mathrm{1}} \left(\mathrm{1}\right)}{\mathrm{1}}\:+\:\frac{{f}^{\mathrm{2}} \left(\mathrm{1}\right)}{\mathrm{2}!}\:+\:...\:+\:\frac{{f}^{\:{n}} \left(\mathrm{1}\right)}{{n}!}\:,\:\mathrm{where} \\ $$$${f}^{\:{r}} \left({x}\right)\:\mathrm{denotes}\:\mathrm{the}\:{r}\mathrm{th}\:\mathrm{order}\:\mathrm{derivative}\:\mathrm{of} \\ $$$${f}\left({x}\right)\:\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:{x}\:,\:\mathrm{is} \\ $$

Commented by sou1618 last updated on 02/Oct/16

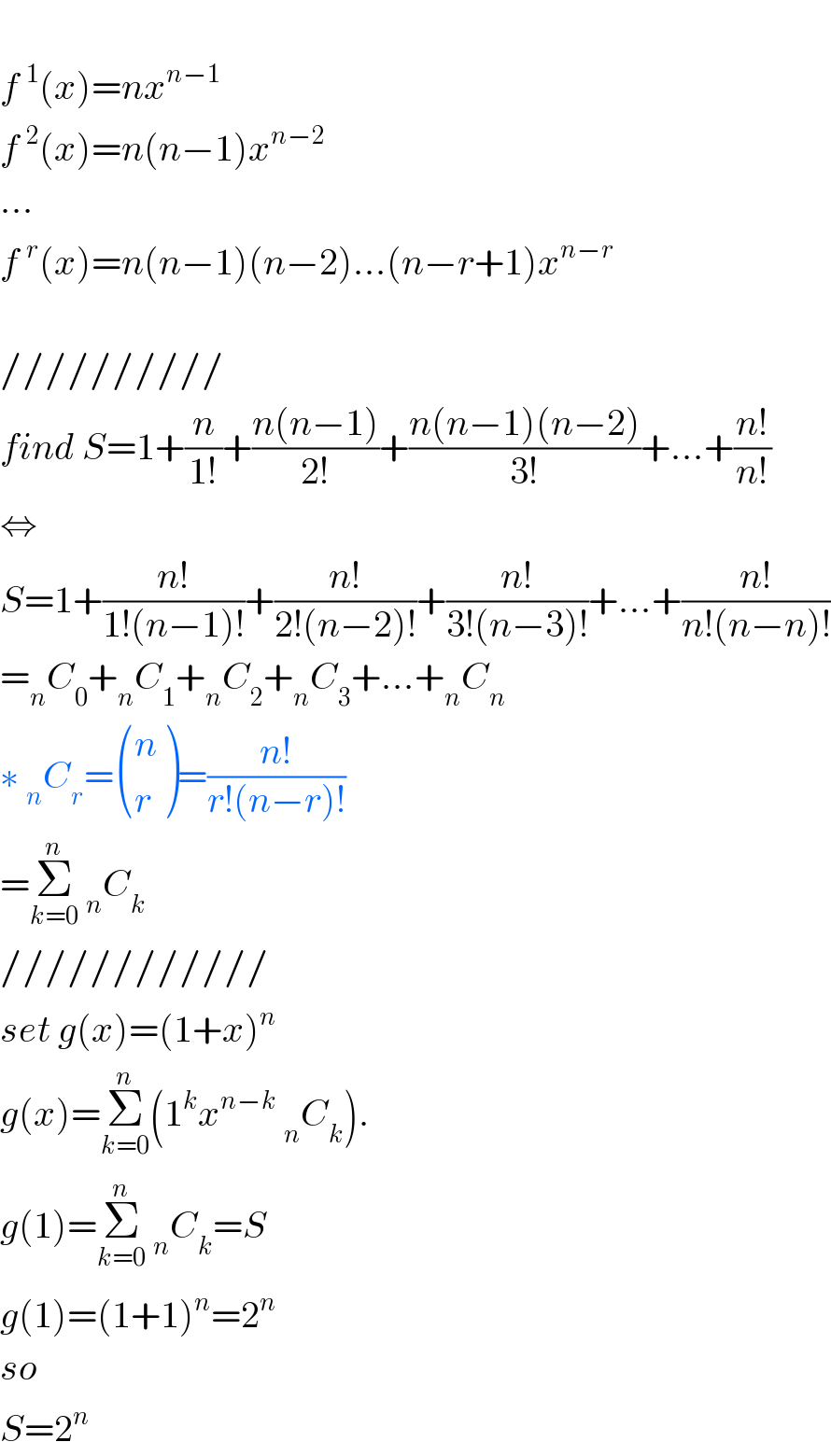
f^1 (x)=nx^(n−1) f^2 (x)=n(n−1)x^(n−2) ... f^r (x)=n(n−1)(n−2)...(n−r+1)x^(n−r) ////////// find S=1+(n/(1!))+((n(n−1))/(2!))+((n(n−1)(n−2))/(3!))+...+((n!)/(n!)) ⇔ S=1+((n!)/(1!(n−1)!))+((n!)/(2!(n−2)!))+((n!)/(3!(n−3)!))+...+((n!)/(n!(n−n)!)) =_n C_0 +_n C_1 +_n C_2 +_n C_3 +...+_n C_n ∗ _n C_r = ((n),(r) )=((n!)/(r!(n−r)!)) =Σ_(k=0) ^n _n C_k //////////// set g(x)=(1+x)^n g(x)=Σ_(k=0) ^n (1^k x^(n−k) _n C_k ). g(1)=Σ_(k=0) ^n _n C_k =S g(1)=(1+1)^n =2^n so S=2^n

$$ \\ $$$${f}\:^{\mathrm{1}} \left({x}\right)={nx}^{{n}−\mathrm{1}} \\ $$$${f}\:^{\mathrm{2}} \left({x}\right)={n}\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} \\ $$$$... \\ $$$${f}\:^{{r}} \left({x}\right)={n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)...\left({n}−{r}+\mathrm{1}\right){x}^{{n}−{r}} \\ $$$$ \\ $$$$////////// \\ $$$${find}\:{S}=\mathrm{1}+\frac{{n}}{\mathrm{1}!}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}+\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{3}!}+...+\frac{{n}!}{{n}!} \\ $$$$\Leftrightarrow \\ $$$${S}=\mathrm{1}+\frac{{n}!}{\mathrm{1}!\left({n}−\mathrm{1}\right)!}+\frac{{n}!}{\mathrm{2}!\left({n}−\mathrm{2}\right)!}+\frac{{n}!}{\mathrm{3}!\left({n}−\mathrm{3}\right)!}+...+\frac{{n}!}{{n}!\left({n}−{n}\right)!} \\ $$$$=_{{n}} {C}_{\mathrm{0}} +_{{n}} {C}_{\mathrm{1}} +_{{n}} {C}_{\mathrm{2}} +_{{n}} {C}_{\mathrm{3}} +...+_{{n}} {C}_{{n}} \\ $$$$\ast\:_{{n}} {C}_{{r}} =\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}=\frac{{n}!}{{r}!\left({n}−{r}\right)!} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:_{{n}} {C}_{{k}} \\ $$$$//////////// \\ $$$${set}\:{g}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{{n}} \\ $$$${g}\left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{1}^{{k}} {x}^{{n}−{k}} \:_{{n}} {C}_{{k}} \right). \\ $$$${g}\left(\mathrm{1}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:_{{n}} {C}_{{k}} ={S} \\ $$$${g}\left(\mathrm{1}\right)=\left(\mathrm{1}+\mathrm{1}\right)^{{n}} =\mathrm{2}^{{n}} \\ $$$${so} \\ $$$${S}=\mathrm{2}^{{n}} \\ $$

Commented by 314159 last updated on 02/Oct/16

Thanks!

$${Thanks}! \\ $$

Answered by prakash jain last updated on 02/Oct/16

Answer in comments

$$\mathrm{Answer}\:\mathrm{in}\:\mathrm{comments} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com