how to prove that the number is divisible by 3, then the number of numbers is a multiple of 3


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 81647 by john santu last updated on 14/Feb/20

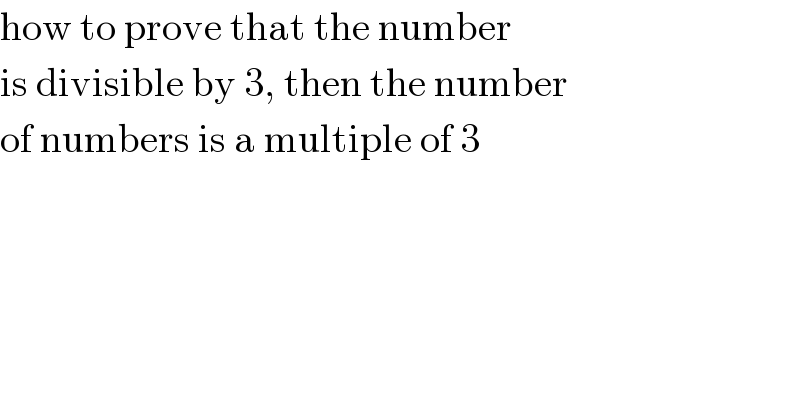
$how to prove that the number$ $is divisible by 3, then the number$ $of numbers is a multiple of 3$
Commented by mr W last updated on 14/Feb/20

$d i d y o u w a n t t o s a y :$ $h o w t o p r o v e t h a t a n u m b e r i s d i v i s i b l e$ $b y 3 w h e n t h e s u m o f i t s d i g i t s i s a$ $m u l t i p l e o f 3 .$ $o r$ $h o w t o p r o v e t h a t, i f a n u m b e r i s d i v i s i b l e$ $b y 3, t h e n t h e s u m o f i t s d i g i t s i s a$ $m u l t i p l e o f 3 .$
Commented by Kunal12588 last updated on 14/Feb/20

$100 a + 10 b + c = 3 q f o r a 3 d i g i t n o .$ $\Rightarrow 3 q = 99 a + 9 b + (a + b + c)$ $\Rightarrow q = 33 a + 3 b + \frac{a + b + c}{3}$ $q \in N \Rightarrow a + b + c ∣ 3$ $f o r a^{'} n^{'} d i g i t n o .$ $3 m = \underset{i = 0}{\sum^{n - 1}} 10^{i} a_{i}; a_{i} i s {(i + 1)}^{t h} d i g i t$ $\Rightarrow m = 3 k + \frac{1}{3} \underset{i = 0}{\sum^{n - 1}} a_{i}$ $\Rightarrow \underset{i = 0}{\sum^{n - 1}} a_{i} i s d i v i s i b l e b y 3 .$ $p l e a s e h e l p m e t o f i n d k$
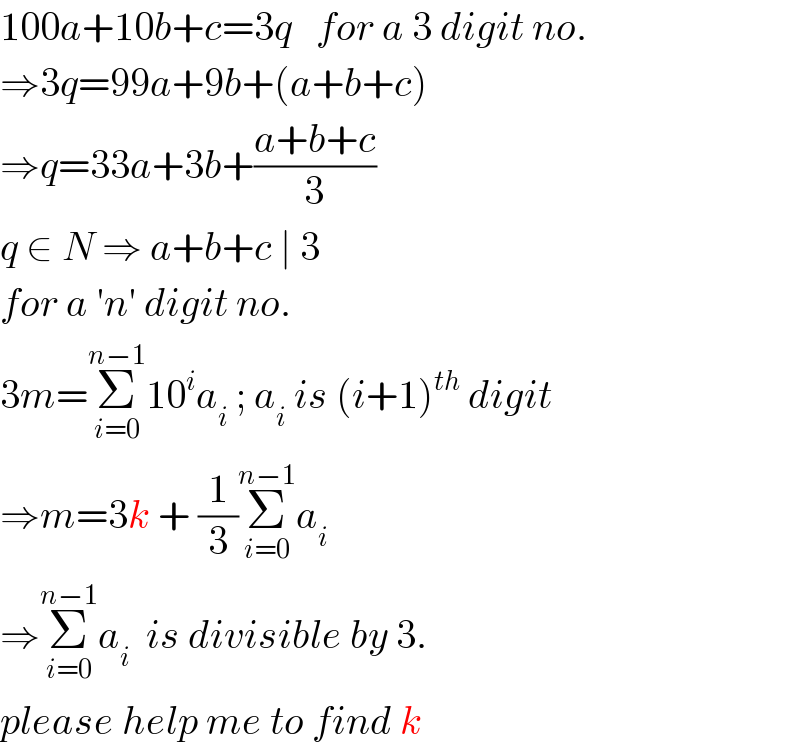
Commented by Prithwish Sen 1 last updated on 14/Feb/20

$a n y n u m b e r c a n b e r e p r e s e n t e d b y$ $N = 10^{n} x_{n} + 10^{n - 1} x_{n - 1} + . . . . . . . . + 10^{2} x_{2} + 10 x_{1} + x_{0}$ $n o w$ $x_{n} + x_{n - 1} + . . . . . . . . . . . + x_{1} + x_{0} = 3 k$ $∴ N = (999 . . . n t i m e s + 1) x_{n} + . . . . . . + (99 + 1) x_{2} + (9 + 1) x_{1} + x_{0}$ $= (999 . . . n t i m e s . x_{n} + . . . . + 99 x_{2} + 9 x_{1}) + (x_{n} + x_{n - 1} + . . . . . + x_{2} + x_{1} + x_{0})$ $= 3 m + 3 k$ $i . e N i s a l s o d i v i s i b l e b y 3 (p r o v e d)$
Commented by mr W last updated on 14/Feb/20

$3 m = \underset{i = 0}{\sum^{n - 1}} 10^{i} a_{i}$ $3 m = \underset{i = 0}{\sum^{n - 1}} {(1 + 9)}^{i} a_{i}$ $3 m = \underset{i = 0}{\sum^{n - 1}} [\underset{k = 0}{\sum^{i}} C_{k}^{i} 9^{k}] a_{i}$ $3 m = \underset{i = 0}{\sum^{n - 1}} [1 + \underset{k = 1}{\sum^{i}} C_{k}^{i} 9^{k}] a_{i}$ $3 m = \underset{i = 0}{\sum^{n - 1}} a_{i} + \underset{i = 1}{\sum^{n - 1}} (\underset{k = 1}{\sum^{i}} C_{k}^{i} 3^{2 k}) a_{i}$ $3 m = \underset{i = 0}{\sum^{n - 1}} a_{i} + 3 h$ $\Rightarrow \underset{i = 0}{\sum^{n - 1}} a_{i} = 3 (m - h) = m u l t i p l e o f 3$
Commented by Prithwish Sen 1 last updated on 14/Feb/20

$H o w a r e y o u s i r ?$
Commented by mr W last updated on 14/Feb/20

$e v e r y t h i n g i s o k w i t h m e, t h a n k s!$ $y o u t o o s i r ?$
Commented by john santu last updated on 14/Feb/20

$yes .$
Commented by Prithwish Sen 1 last updated on 15/Feb/20

$f i n e s i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum