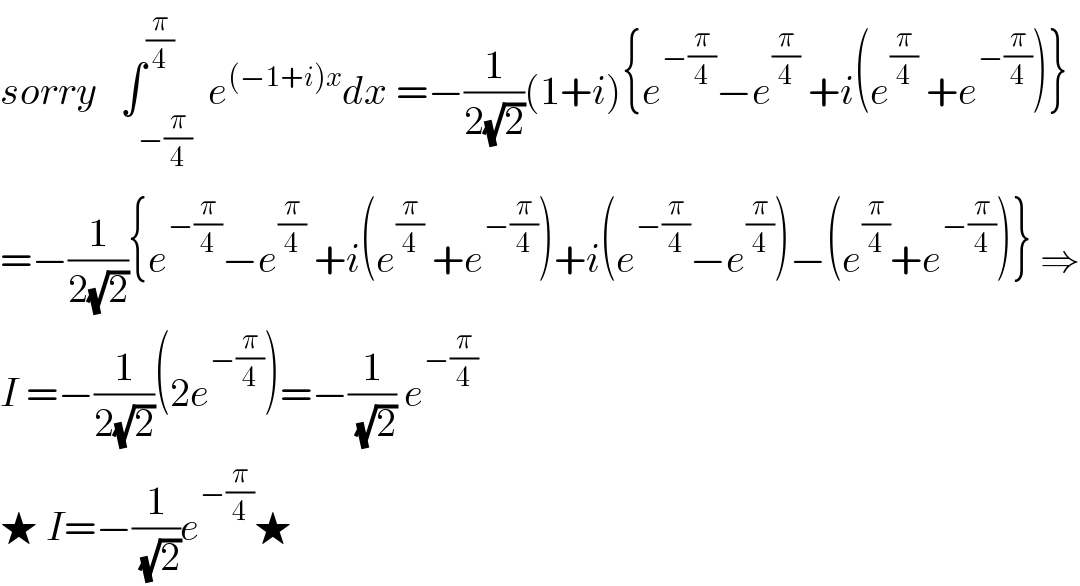Question Number 81664 by zainal tanjung last updated on 14/Feb/20
$$\underset{−\pi/\mathrm{4}} {\overset{\pi/\mathrm{4}} {\int}}\:{e}^{−{x}} \:\mathrm{sin}\:{x}\:{dx}\:= \\ $$
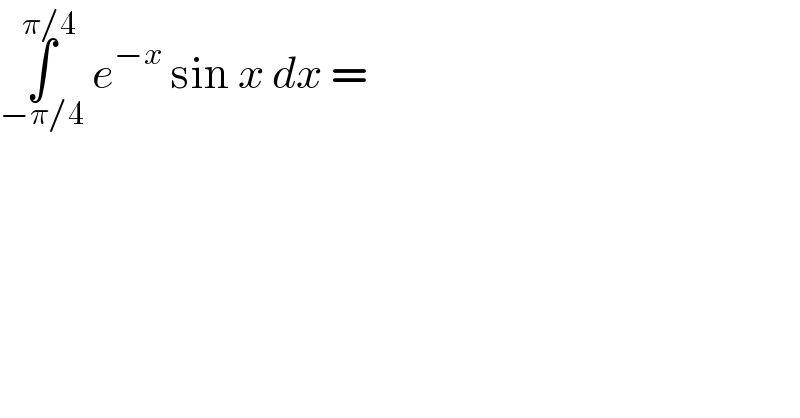
Commented by zainal tanjung last updated on 14/Feb/20
$$ \\ $$
Commented by abdomathmax last updated on 14/Feb/20
![I=Im(∫_(−(π/4)) ^(π/4) e^(−x) e^(ix) dx)=Im(∫_(−(π/4)) ^(π/4) e^((−1+i)x) dx) and ∫_(−(π/4)) ^(π/4) e^((−1+i)x) dx=[(1/(−1+i))e^((−1+i)x) ]_(−(π/4)) ^(π/4) =((−1)/(1−i)){ e^((−1+i)(π/4)) −e^(−(−1+i)(π/4)) } =((−1−i)/2){ e^(−(π/4)) ((1/(√2))+(i/(√2)))−e^(π/4) ((1/(√2))−(i/(√2)))} =−((1+i)/2){(1/(√2))(e^(−(π/4)) −e^(π/4) )+(i/(√2))(e^(π/4) +e^(−(π/4)) )} =−(1/(√2))(1+i){ e^(−(π/4)) −e^(π/4) +(e^(π/4) +e^(−(π/4)) )i} =−(1/(√2)){e^(−(π/4)) −e^(π/4) +i(e^(π/4) +e^(−(π/4)) )+i(e^(−(π/4)) −e^(π/4) ) −(e^(π/4) −e^(−(π/4)) )} =−(1/(√2)){2e^(−(π/4)) −2e^(π/4) +i(2e^(−(π/4)) )} ⇒ I =2 e^(−(π/4))](Q81668.png)
$${I}={Im}\left(\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} {e}^{−{x}} \:{e}^{{ix}} {dx}\right)={Im}\left(\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:{e}^{\left(−\mathrm{1}+{i}\right){x}} {dx}\right) \\ $$$${and}\:\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:{e}^{\left(−\mathrm{1}+{i}\right){x}} {dx}=\left[\frac{\mathrm{1}}{−\mathrm{1}+{i}}{e}^{\left(−\mathrm{1}+{i}\right){x}} \right]_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{1}−{i}}\left\{\:{e}^{\left(−\mathrm{1}+{i}\right)\frac{\pi}{\mathrm{4}}} −{e}^{−\left(−\mathrm{1}+{i}\right)\frac{\pi}{\mathrm{4}}} \right\} \\ $$$$=\frac{−\mathrm{1}−{i}}{\mathrm{2}}\left\{\:{e}^{−\frac{\pi}{\mathrm{4}}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+\frac{{i}}{\sqrt{\mathrm{2}}}\right)−{e}^{\frac{\pi}{\mathrm{4}}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}−\frac{{i}}{\sqrt{\mathrm{2}}}\right)\right\} \\ $$$$=−\frac{\mathrm{1}+{i}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left({e}^{−\frac{\pi}{\mathrm{4}}} −{e}^{\frac{\pi}{\mathrm{4}}} \right)+\frac{{i}}{\sqrt{\mathrm{2}}}\left({e}^{\frac{\pi}{\mathrm{4}}} +{e}^{−\frac{\pi}{\mathrm{4}}} \right)\right\} \\ $$$$=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left(\mathrm{1}+{i}\right)\left\{\:{e}^{−\frac{\pi}{\mathrm{4}}} −{e}^{\frac{\pi}{\mathrm{4}}} \:+\left({e}^{\frac{\pi}{\mathrm{4}}} +{e}^{−\frac{\pi}{\mathrm{4}}} \right){i}\right\} \\ $$$$=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left\{{e}^{−\frac{\pi}{\mathrm{4}}} −{e}^{\frac{\pi}{\mathrm{4}}} \:+{i}\left({e}^{\frac{\pi}{\mathrm{4}}} +{e}^{−\frac{\pi}{\mathrm{4}}} \right)+{i}\left({e}^{−\frac{\pi}{\mathrm{4}}} −{e}^{\frac{\pi}{\mathrm{4}}} \right)\right. \\ $$$$\left.−\left({e}^{\frac{\pi}{\mathrm{4}}} −{e}^{−\frac{\pi}{\mathrm{4}}} \right)\right\}\:=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left\{\mathrm{2}{e}^{−\frac{\pi}{\mathrm{4}}} −\mathrm{2}{e}^{\frac{\pi}{\mathrm{4}}} \right. \\ $$$$\left.+{i}\left(\mathrm{2}{e}^{−\frac{\pi}{\mathrm{4}}} \right)\right\}\:\Rightarrow\:{I}\:=\mathrm{2}\:{e}^{−\frac{\pi}{\mathrm{4}}} \\ $$
Commented by Tony Lin last updated on 14/Feb/20
![∫e^(−x) sinxdx =−e^(−x) sinx+∫e^(−x) cosxdx =−e^(−x) sinx+(−e^(−x) cosx−∫e^(−x) sinxdx) ⇒∫e^(−x) sinxdx =((−e^(−x) (sinx+cosx))/2)+c ⇒∫_(−(π/4)) ^(π/4) e^(−x) sinxdx =[((−e^(−x) (sinx+cosx))/2)]_(−(π/4)) ^(π/4) =−(e^(−(π/4)) /(√2))](Q81675.png)
$$\int{e}^{−{x}} {sinxdx}\: \\ $$$$=−{e}^{−{x}} {sinx}+\int{e}^{−{x}} {cosxdx} \\ $$$$=−{e}^{−{x}} {sinx}+\left(−{e}^{−{x}} {cosx}−\int{e}^{−{x}} {sinxdx}\right) \\ $$$$\Rightarrow\int{e}^{−{x}} {sinxdx} \\ $$$$=\frac{−{e}^{−{x}} \left({sinx}+{cosx}\right)}{\mathrm{2}}+{c} \\ $$$$\Rightarrow\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} {e}^{−{x}} {sinxdx} \\ $$$$=\left[\frac{−{e}^{−{x}} \left({sinx}+{cosx}\right)}{\mathrm{2}}\right]_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=−\frac{{e}^{−\frac{\pi}{\mathrm{4}}} }{\sqrt{\mathrm{2}}} \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20
$${sorry}\:\:\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:{e}^{\left(−\mathrm{1}+{i}\right){x}} {dx}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\mathrm{1}+{i}\right)\left\{{e}^{−\frac{\pi}{\mathrm{4}}} −{e}^{\frac{\pi}{\mathrm{4}}} \:+{i}\left({e}^{\frac{\pi}{\mathrm{4}}} \:+{e}^{−\frac{\pi}{\mathrm{4}}} \right)\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{{e}^{−\frac{\pi}{\mathrm{4}}} −{e}^{\frac{\pi}{\mathrm{4}}} \:+{i}\left({e}^{\frac{\pi}{\mathrm{4}}} \:+{e}^{−\frac{\pi}{\mathrm{4}}} \right)+{i}\left({e}^{−\frac{\pi}{\mathrm{4}}} −{e}^{\frac{\pi}{\mathrm{4}}} \right)−\left({e}^{\frac{\pi}{\mathrm{4}}} +{e}^{−\frac{\pi}{\mathrm{4}}} \right)\right\}\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\mathrm{2}{e}^{−\frac{\pi}{\mathrm{4}}} \right)=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:{e}^{−\frac{\pi}{\mathrm{4}}} \\ $$$$\bigstar\:{I}=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{\pi}{\mathrm{4}}} \bigstar \\ $$