
Question and Answers Forum
Question Number 81672 by zainal tanjung last updated on 14/Feb/20
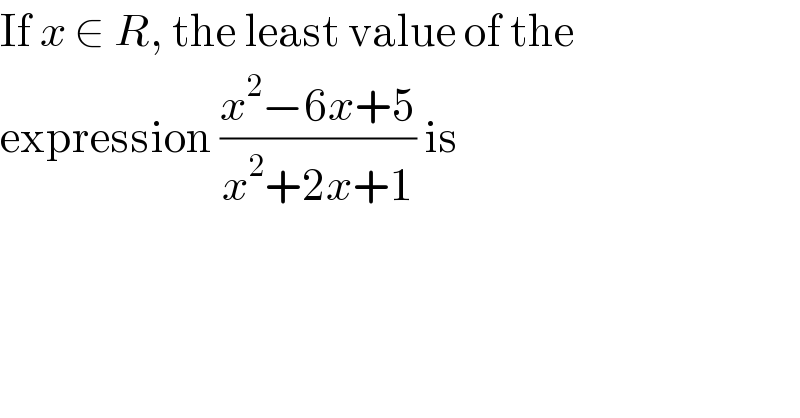
Commented by Kunal12588 last updated on 14/Feb/20
![y=(((x−5)(x−1))/((x+1)^2 )) (dy/dx)=(((x+1)^2 [(x−5)+(x−1)]−(x−5)(x−1)[2(x+1)])/((x+1)^4 )) ⇒(dy/dx)=((2(x^2 +2x+1)(x−3)−2(x−5)(x^2 −1))/((x+1)^4 )) ⇒(dy/dx)=((2[x^3 +2x^2 +x−3x^2 −6x−3−(x^3 −5x^2 −x+5)])/((x+1)^4 )) ⇒(dy/dx)=((2(4x^2 −4x−8))/((x+1)^4 )) ⇒(dy/dx)=((8(x^2 −x−2))/((x+1)^4 )) ⇒(dy/dx)=((8(x−2)(x+1))/((x+1)^4 )) for max or min (dy/dx)=0⇒x=2, x≠−1 (d^2 y/dx^2 )>0 when x=2 y_(local min) =(((2−5)(2−1))/((2+1)^2 ))=((−3)/3^2 )=−(1/3)=−0.3^(−)](Q81680.png)
Commented by Tony Lin last updated on 14/Feb/20
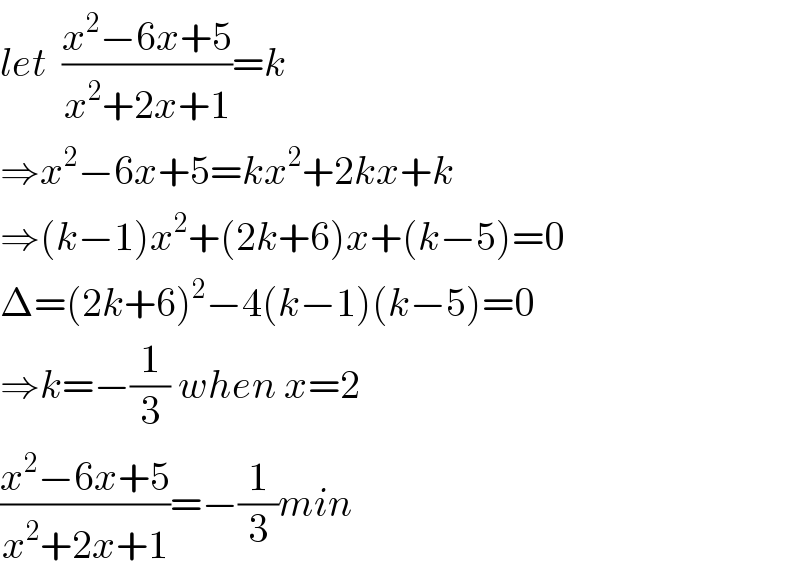
Commented by mathmax by abdo last updated on 14/Feb/20

| ||
Question and Answers Forum | ||
Question Number 81672 by zainal tanjung last updated on 14/Feb/20 | ||
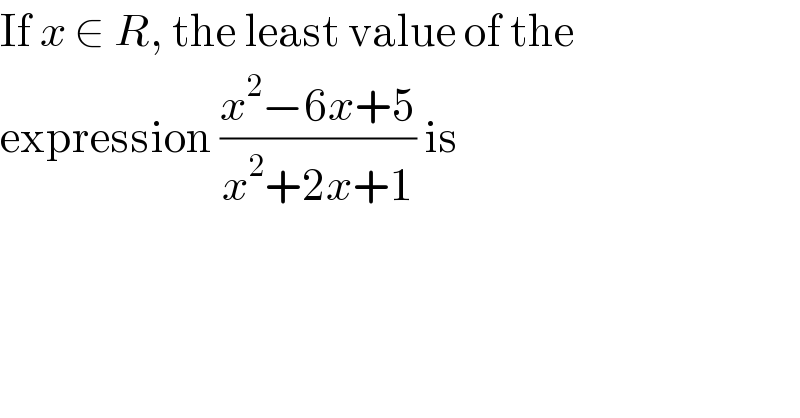 | ||
Commented by Kunal12588 last updated on 14/Feb/20 | ||
![y=(((x−5)(x−1))/((x+1)^2 )) (dy/dx)=(((x+1)^2 [(x−5)+(x−1)]−(x−5)(x−1)[2(x+1)])/((x+1)^4 )) ⇒(dy/dx)=((2(x^2 +2x+1)(x−3)−2(x−5)(x^2 −1))/((x+1)^4 )) ⇒(dy/dx)=((2[x^3 +2x^2 +x−3x^2 −6x−3−(x^3 −5x^2 −x+5)])/((x+1)^4 )) ⇒(dy/dx)=((2(4x^2 −4x−8))/((x+1)^4 )) ⇒(dy/dx)=((8(x^2 −x−2))/((x+1)^4 )) ⇒(dy/dx)=((8(x−2)(x+1))/((x+1)^4 )) for max or min (dy/dx)=0⇒x=2, x≠−1 (d^2 y/dx^2 )>0 when x=2 y_(local min) =(((2−5)(2−1))/((2+1)^2 ))=((−3)/3^2 )=−(1/3)=−0.3^(−)](Q81680.png) | ||
Commented by Tony Lin last updated on 14/Feb/20 | ||
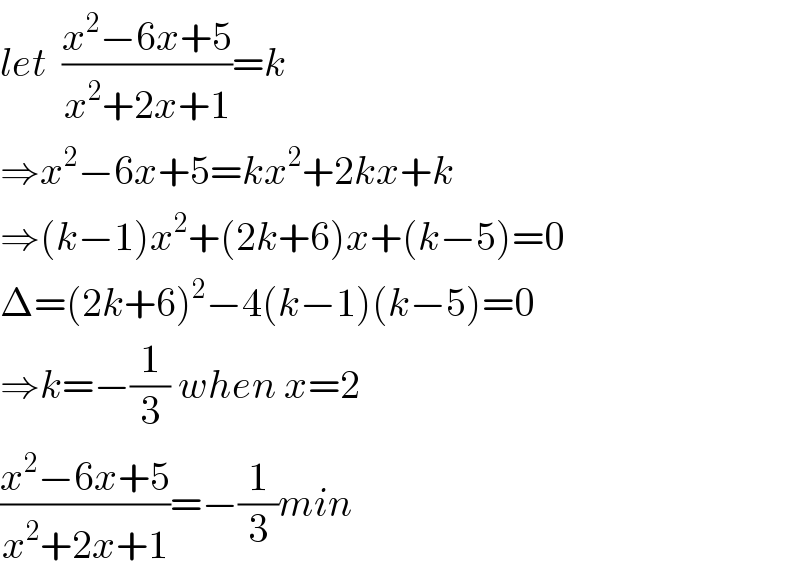 | ||
Commented by mathmax by abdo last updated on 14/Feb/20 | ||
 | ||