
Question and Answers Forum
Question Number 81684 by naka3546 last updated on 14/Feb/20
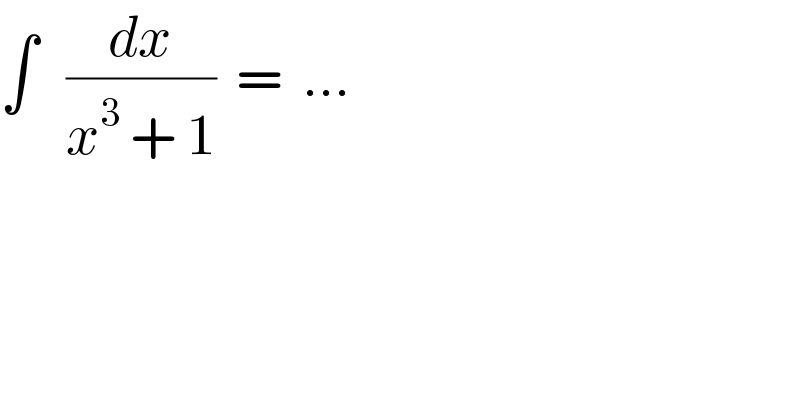
Commented by Tony Lin last updated on 14/Feb/20
![∫ (dx/(x^3 +1)) =∫(dx/((x+1)(x^2 −x+1))) =(1/3)∫(1/(x+1 ))dx−(1/3)∫((x−2)/(x^2 −x+1))dx =(1/3)ln∣x+1∣−(1/3)[∫(((1/2)(2x−1))/(x^2 −x+1)) dx−(3/2)∫(dx/((x−(1/2))^2 +(3/4)))] =(1/3)ln∣x+1∣−(1/6)ln∣x^2 −x+1∣+(√3)tan^(−1) (((2x−1)/(√3)))+c](Q81687.png)
Answered by TANMAY PANACEA last updated on 14/Feb/20

Commented by peter frank last updated on 14/Feb/20
| ||
Question and Answers Forum | ||
Question Number 81684 by naka3546 last updated on 14/Feb/20 | ||
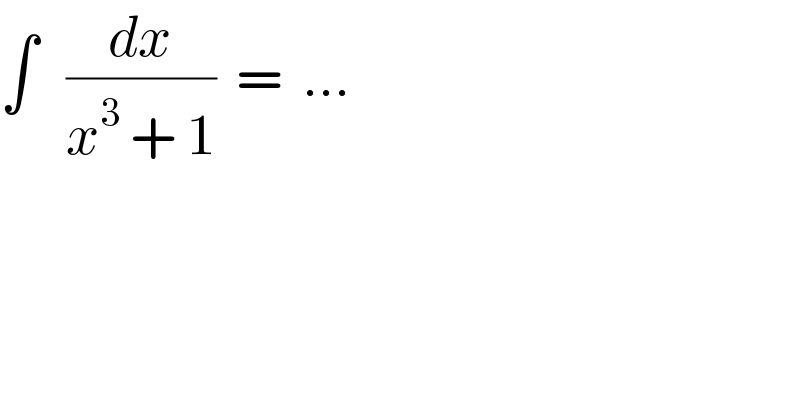 | ||
Commented by Tony Lin last updated on 14/Feb/20 | ||
![∫ (dx/(x^3 +1)) =∫(dx/((x+1)(x^2 −x+1))) =(1/3)∫(1/(x+1 ))dx−(1/3)∫((x−2)/(x^2 −x+1))dx =(1/3)ln∣x+1∣−(1/3)[∫(((1/2)(2x−1))/(x^2 −x+1)) dx−(3/2)∫(dx/((x−(1/2))^2 +(3/4)))] =(1/3)ln∣x+1∣−(1/6)ln∣x^2 −x+1∣+(√3)tan^(−1) (((2x−1)/(√3)))+c](Q81687.png) | ||
Answered by TANMAY PANACEA last updated on 14/Feb/20 | ||
 | ||
| ||
Commented by peter frank last updated on 14/Feb/20 | ||
 | ||