
Question and Answers Forum
Question Number 81733 by naka3546 last updated on 15/Feb/20
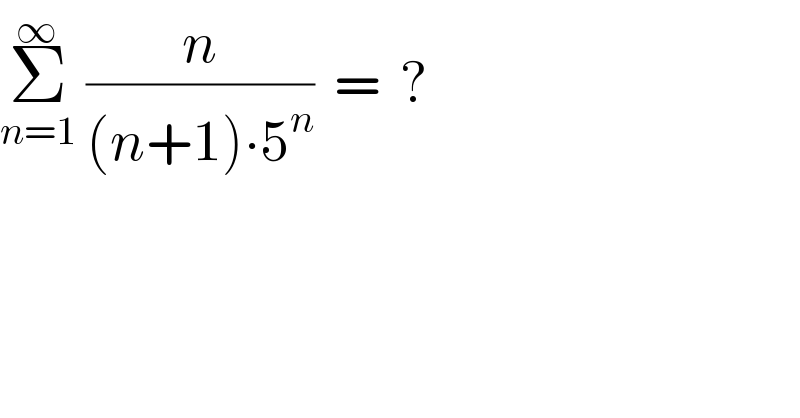
Commented by mr W last updated on 15/Feb/20
![(1/(1−x))=1+x+x^2 +x^3 +...=Σ_(n=0) ^∞ x^n (1/((1−x)^2 ))=Σ_(n=1) ^∞ nx^(n−1) (x/((1−x)^2 ))=Σ_(n=1) ^∞ nx^n ∫_0 ^x (x/((1−x)^2 ))dx=Σ_(n=1) ^∞ n∫_0 ^x x^n dx [ln (1−x)+(1/(1−x))]_0 ^x =Σ_(n=1) ^∞ ((nx^(n+1) )/(n+1)) ln (1−x)+(x/(1−x))=Σ_(n=1) ^∞ ((nx^(n+1) )/(n+1)) ((ln (1−x))/x)+(1/(1−x))=Σ_(n=1) ^∞ ((nx^n )/(n+1)) x=(1/5) 5(ln (4/5)+(1/4))=Σ_(n=1) ^∞ (n/((n+1)5^n ))](Q81746.png)
Commented by mathmax by abdo last updated on 15/Feb/20
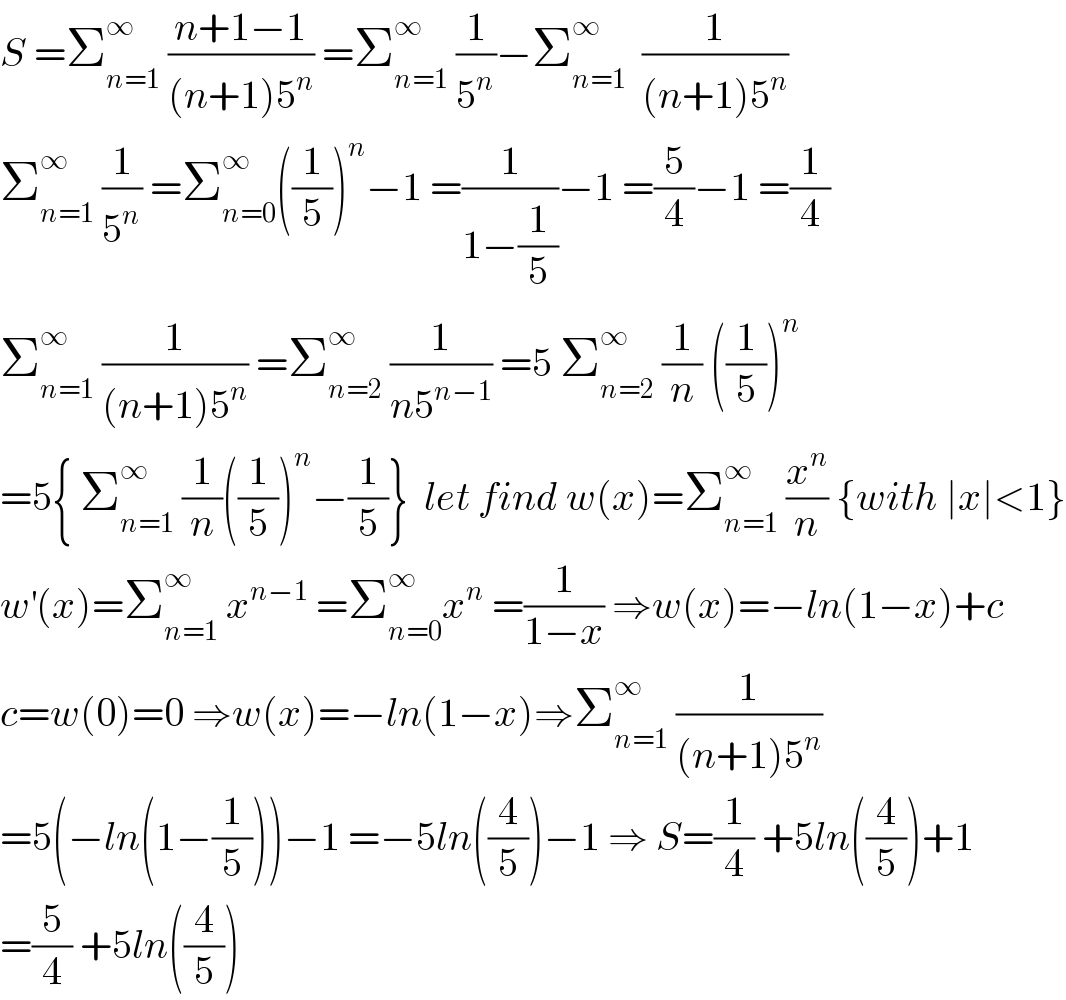
| ||
Question and Answers Forum | ||
Question Number 81733 by naka3546 last updated on 15/Feb/20 | ||
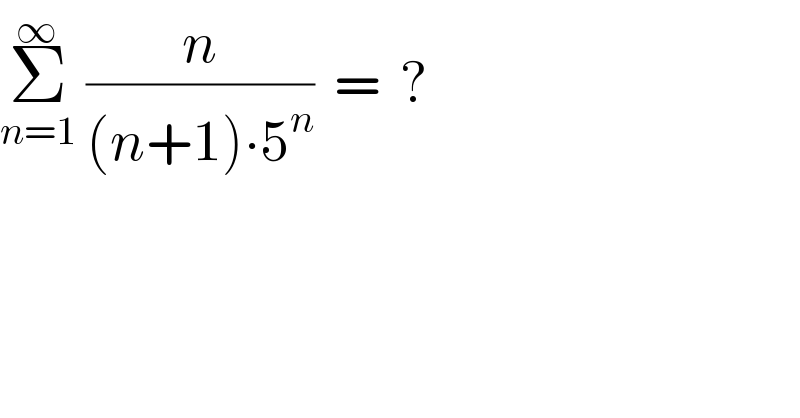 | ||
Commented by mr W last updated on 15/Feb/20 | ||
![(1/(1−x))=1+x+x^2 +x^3 +...=Σ_(n=0) ^∞ x^n (1/((1−x)^2 ))=Σ_(n=1) ^∞ nx^(n−1) (x/((1−x)^2 ))=Σ_(n=1) ^∞ nx^n ∫_0 ^x (x/((1−x)^2 ))dx=Σ_(n=1) ^∞ n∫_0 ^x x^n dx [ln (1−x)+(1/(1−x))]_0 ^x =Σ_(n=1) ^∞ ((nx^(n+1) )/(n+1)) ln (1−x)+(x/(1−x))=Σ_(n=1) ^∞ ((nx^(n+1) )/(n+1)) ((ln (1−x))/x)+(1/(1−x))=Σ_(n=1) ^∞ ((nx^n )/(n+1)) x=(1/5) 5(ln (4/5)+(1/4))=Σ_(n=1) ^∞ (n/((n+1)5^n ))](Q81746.png) | ||
Commented by mathmax by abdo last updated on 15/Feb/20 | ||
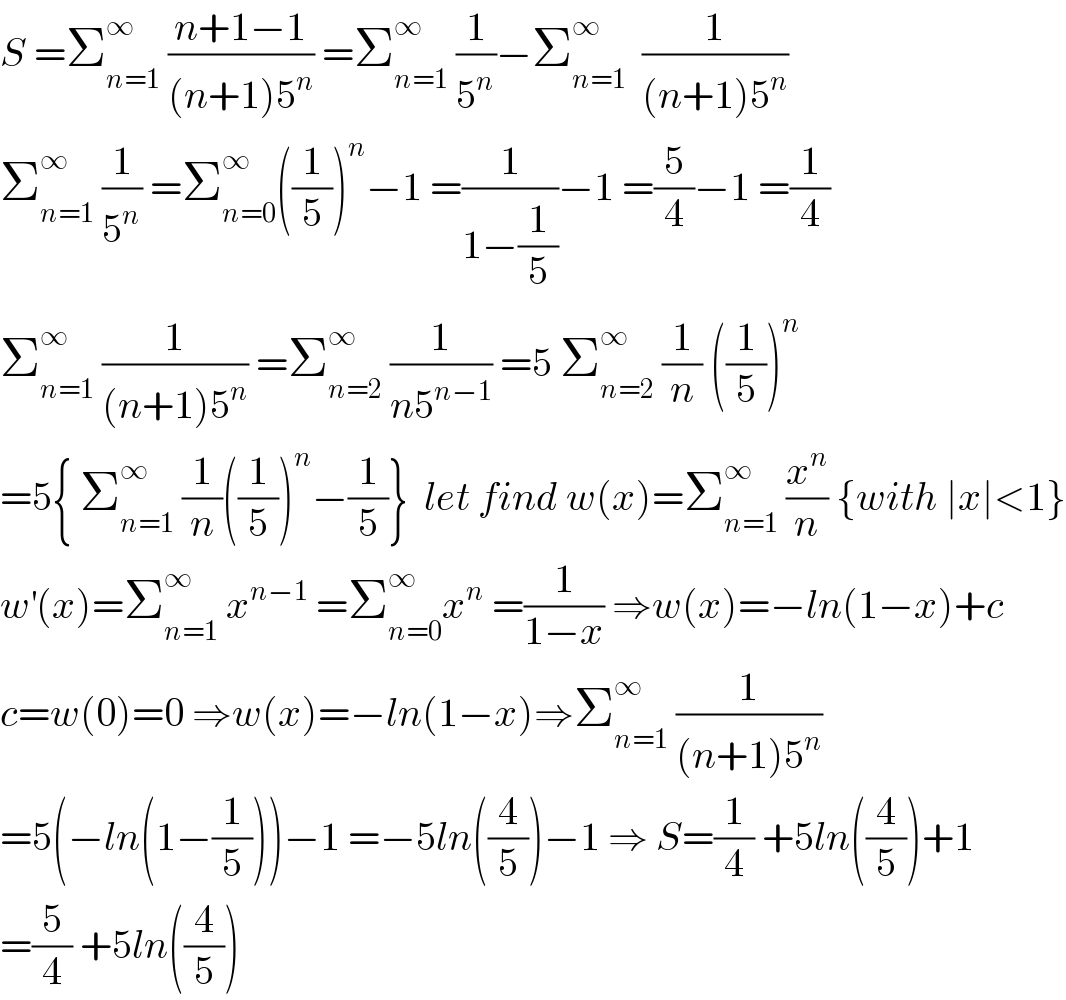 | ||