Question Number 81804 by ajfour last updated on 15/Feb/20
Commented by ajfour last updated on 15/Feb/20
$${If}\:{tension}\:{in}\:{string},\:{T}=\frac{{mg}}{\mathrm{5}} \\ $$$${and}\:{rod}\:{rests}\:{in}\:{equilibrium}, \\ $$$${find}\:{length}\:{of}\:{string}. \\ $$
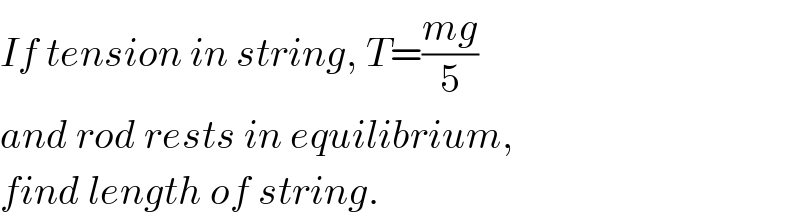
Answered by mr W last updated on 15/Feb/20
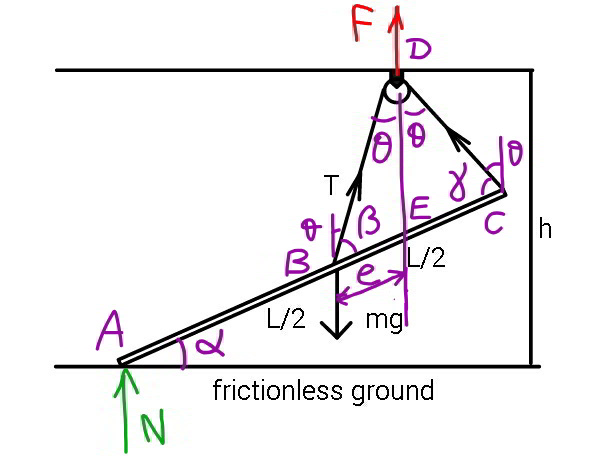
Commented by mr W last updated on 16/Feb/20
![β+θ=(π/2)−α ⇒β=(π/2)−(θ+α) γ+θ=(π/2)+α ⇒γ=(π/2)−(θ−α) ((BD)/(sin γ))=((DC)/(sin β))=((BC)/(sin 2θ)) BD=((L sin γ)/(2 sin 2θ))=((L cos (θ−α))/(2 sin 2θ)) DC=((L sin β)/(2 sin 2θ))=((L cos (θ+α))/(2 sin 2θ)) l=BD+DC=((L[cos (θ−α)+cos (θ+α)])/(2 sin 2θ)) ⇒l=((L cos α)/(2 sin θ)) ...(iii) BD sin θ=e cos α ((L cos (θ−α) sin θ)/(2 sin 2θ))=e cos α e=((L cos (θ−α))/(4 cos θ cos α))=(L/4)(1+tan θ tan α) let T=((mg)/τ) with τ=5 given F=2T cos θ F((L/2)+e)=mg×(L/2) ⇒3 cos θ+sin θ tan α=τ ...(i) ((L sin α)/2)+BD×cos θ=h 2 sin α+((cos (θ−α))/(sin θ))=((4h)/L) with η=(h/L) ⇒3 sin α+((cos α)/(tan θ))=4η ...(ii) from (i): (3/(√(9+tan^2 α))) cos θ+sin θ ((tan α)/(√(9+tan^2 α)))=(τ/(√(9+tan^2 α))) cos (θ−φ)=(τ/(√(9+tan^2 α))) with tan φ=((tan α)/3) ⇒θ=tan^(−1) (((tan α)/3))+cos^(−1) ((τ/(√(9+tan^2 α)))) put this into (ii) we can get α. with α and θ, we get the length of the string acc. to (iii): l=((L cos α)/(2 sin θ)). example: τ=((mg)/T)=3, η=(h/L)=(4/5)=0.80 ⇒α=39.6988° ⇒θ=30.9364° ⇒l=3.7416m =================== if string length l is given, find T=? from (iii) we get ((cos α)/(sin θ))=((2l)/L)=λ ⇒sin θ=((cos α)/λ) put this into (ii): 3 sin α+(√(λ^2 −cos^2 α))=4η (√(λ^2 −1+sin^2 α))=4η−3 sin α 8 sin^2 α−24η sin α+16η^2 +1−λ^2 =0 ⇒sin α=((6η−(√(2(2η^2 +λ^2 −1))))/4) with α and θ we can get from (i): τ=3 cos θ+sin θ tan α ⇒τ=(1/λ)(3(√(λ^2 −1+sin^2 α))+sin α) example: L=4m, h=3m, l=3m η=(h/L)=(3/4)=0.75, λ=((2l)/L)=(6/4)=1.5 sin α=((6η−(√(2(2η^2 +λ^2 −1))))/4)=0.580137 ⇒τ=2.905932 ⇒T=((mg)/τ)=0.344mg](Q81834.png)
$$\beta+\theta=\frac{\pi}{\mathrm{2}}−\alpha \\ $$$$\Rightarrow\beta=\frac{\pi}{\mathrm{2}}−\left(\theta+\alpha\right) \\ $$$$\gamma+\theta=\frac{\pi}{\mathrm{2}}+\alpha \\ $$$$\Rightarrow\gamma=\frac{\pi}{\mathrm{2}}−\left(\theta−\alpha\right) \\ $$$$ \\ $$$$\frac{{BD}}{\mathrm{sin}\:\gamma}=\frac{{DC}}{\mathrm{sin}\:\beta}=\frac{{BC}}{\mathrm{sin}\:\mathrm{2}\theta} \\ $$$${BD}=\frac{{L}\:\mathrm{sin}\:\gamma}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta}=\frac{{L}\:\mathrm{cos}\:\left(\theta−\alpha\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$${DC}=\frac{{L}\:\mathrm{sin}\:\beta}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta}=\frac{{L}\:\mathrm{cos}\:\left(\theta+\alpha\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$${l}={BD}+{DC}=\frac{{L}\left[\mathrm{cos}\:\left(\theta−\alpha\right)+\mathrm{cos}\:\left(\theta+\alpha\right)\right]}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\Rightarrow{l}=\frac{{L}\:\mathrm{cos}\:\alpha}{\mathrm{2}\:\mathrm{sin}\:\theta}\:\:\:...\left({iii}\right) \\ $$$$ \\ $$$${BD}\:\mathrm{sin}\:\theta={e}\:\mathrm{cos}\:\alpha \\ $$$$\frac{{L}\:\mathrm{cos}\:\left(\theta−\alpha\right)\:\mathrm{sin}\:\theta}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta}={e}\:\mathrm{cos}\:\alpha \\ $$$${e}=\frac{{L}\:\mathrm{cos}\:\left(\theta−\alpha\right)}{\mathrm{4}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\alpha}=\frac{{L}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{tan}\:\theta\:\mathrm{tan}\:\alpha\right) \\ $$$$ \\ $$$${let}\:{T}=\frac{{mg}}{\tau}\:{with}\:\tau=\mathrm{5}\:{given} \\ $$$${F}=\mathrm{2}{T}\:\mathrm{cos}\:\theta \\ $$$${F}\left(\frac{{L}}{\mathrm{2}}+{e}\right)={mg}×\frac{{L}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{3}\:\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\:\mathrm{tan}\:\alpha=\tau\:\:\:...\left({i}\right) \\ $$$$ \\ $$$$\frac{{L}\:\mathrm{sin}\:\alpha}{\mathrm{2}}+{BD}×\mathrm{cos}\:\theta={h} \\ $$$$\mathrm{2}\:\mathrm{sin}\:\alpha+\frac{\mathrm{cos}\:\left(\theta−\alpha\right)}{\mathrm{sin}\:\theta}=\frac{\mathrm{4}{h}}{{L}} \\ $$$${with}\:\eta=\frac{{h}}{{L}} \\ $$$$\Rightarrow\mathrm{3}\:\mathrm{sin}\:\alpha+\frac{\mathrm{cos}\:\alpha}{\mathrm{tan}\:\theta}=\mathrm{4}\eta\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right): \\ $$$$\frac{\mathrm{3}}{\sqrt{\mathrm{9}+\mathrm{tan}^{\mathrm{2}} \:\alpha}}\:\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\:\frac{\mathrm{tan}\:\alpha}{\sqrt{\mathrm{9}+\mathrm{tan}^{\mathrm{2}} \:\alpha}}=\frac{\tau}{\sqrt{\mathrm{9}+\mathrm{tan}^{\mathrm{2}} \:\alpha}} \\ $$$$\mathrm{cos}\:\left(\theta−\phi\right)=\frac{\tau}{\sqrt{\mathrm{9}+\mathrm{tan}^{\mathrm{2}} \:\alpha}}\:{with}\:\mathrm{tan}\:\phi=\frac{\mathrm{tan}\:\alpha}{\mathrm{3}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\alpha}{\mathrm{3}}\right)+\mathrm{cos}^{−\mathrm{1}} \left(\frac{\tau}{\sqrt{\mathrm{9}+\mathrm{tan}^{\mathrm{2}} \:\alpha}}\right) \\ $$$${put}\:{this}\:{into}\:\left({ii}\right)\:{we}\:{can}\:{get}\:\alpha. \\ $$$$ \\ $$$${with}\:\alpha\:{and}\:\theta,\:{we}\:{get}\:{the}\:{length}\:{of} \\ $$$${the}\:{string}\:{acc}.\:{to}\:\left({iii}\right):\:{l}=\frac{{L}\:\mathrm{cos}\:\alpha}{\mathrm{2}\:\mathrm{sin}\:\theta}. \\ $$$$ \\ $$$${example}:\:\tau=\frac{{mg}}{{T}}=\mathrm{3},\:\eta=\frac{{h}}{{L}}=\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{0}.\mathrm{80} \\ $$$$\Rightarrow\alpha=\mathrm{39}.\mathrm{6988}° \\ $$$$\Rightarrow\theta=\mathrm{30}.\mathrm{9364}° \\ $$$$\Rightarrow{l}=\mathrm{3}.\mathrm{7416}{m} \\ $$$$=================== \\ $$$${if}\:{string}\:{length}\:{l}\:{is}\:{given},\:{find}\:{T}=? \\ $$$${from}\:\left({iii}\right)\:{we}\:{get} \\ $$$$\frac{\mathrm{cos}\:\alpha}{\mathrm{sin}\:\theta}=\frac{\mathrm{2}{l}}{{L}}=\lambda \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{cos}\:\alpha}{\lambda} \\ $$$${put}\:{this}\:{into}\:\left({ii}\right): \\ $$$$\mathrm{3}\:\mathrm{sin}\:\alpha+\sqrt{\lambda^{\mathrm{2}} −\mathrm{cos}^{\mathrm{2}} \:\alpha}=\mathrm{4}\eta \\ $$$$\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\alpha}=\mathrm{4}\eta−\mathrm{3}\:\mathrm{sin}\:\alpha \\ $$$$\mathrm{8}\:\mathrm{sin}^{\mathrm{2}} \:\alpha−\mathrm{24}\eta\:\mathrm{sin}\:\alpha+\mathrm{16}\eta^{\mathrm{2}} +\mathrm{1}−\lambda^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{6}\eta−\sqrt{\mathrm{2}\left(\mathrm{2}\eta^{\mathrm{2}} +\lambda^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{4}} \\ $$$${with}\:\alpha\:{and}\:\theta\:{we}\:{can}\:{get}\:{from}\:\left({i}\right): \\ $$$$\tau=\mathrm{3}\:\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\:\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\tau=\frac{\mathrm{1}}{\lambda}\left(\mathrm{3}\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\alpha}+\mathrm{sin}\:\alpha\right) \\ $$$$ \\ $$$${example}:\:{L}=\mathrm{4}{m},\:{h}=\mathrm{3}{m},\:{l}=\mathrm{3}{m} \\ $$$$\eta=\frac{{h}}{{L}}=\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{0}.\mathrm{75},\:\lambda=\frac{\mathrm{2}{l}}{{L}}=\frac{\mathrm{6}}{\mathrm{4}}=\mathrm{1}.\mathrm{5} \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{6}\eta−\sqrt{\mathrm{2}\left(\mathrm{2}\eta^{\mathrm{2}} +\lambda^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{4}}=\mathrm{0}.\mathrm{580137} \\ $$$$\Rightarrow\tau=\mathrm{2}.\mathrm{905932} \\ $$$$\Rightarrow{T}=\frac{{mg}}{\tau}=\mathrm{0}.\mathrm{344}{mg} \\ $$
Commented by ajfour last updated on 15/Feb/20
$${great}\:{way}\:{Sir},\:{its}\:{really}\:{not}\:{so} \\ $$$${complex},\:{thank}\:{you},\:{i}\:{think} \\ $$$${my}\:{solution}\:{answers}\:{well}\:{too}. \\ $$
Commented by mr W last updated on 15/Feb/20
$${that}'{s}\:{sure}\:{sir}!\:{your}\:{solution}\:{solves} \\ $$$${the}\:{problem}\:{also}\:{very}\:{well}.\:{many} \\ $$$${ways}\:{lead}\:{to}\:{the}\:{same}\:{goal}! \\ $$
Commented by mr W last updated on 16/Feb/20
$${for}\:{the}\:{case}:\:{l}\:{is}\:{given},\:{find}\:{T}=? \\ $$$${an}\:{exact}\:{solution}\:{is}\:{possible},\:{see}\:{above}. \\ $$
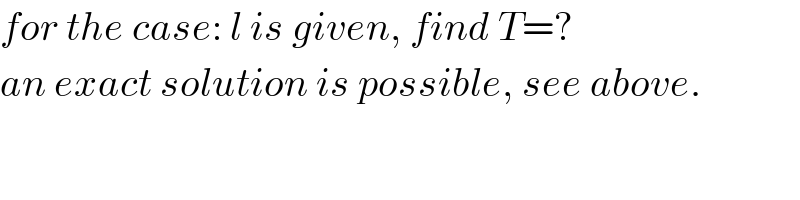
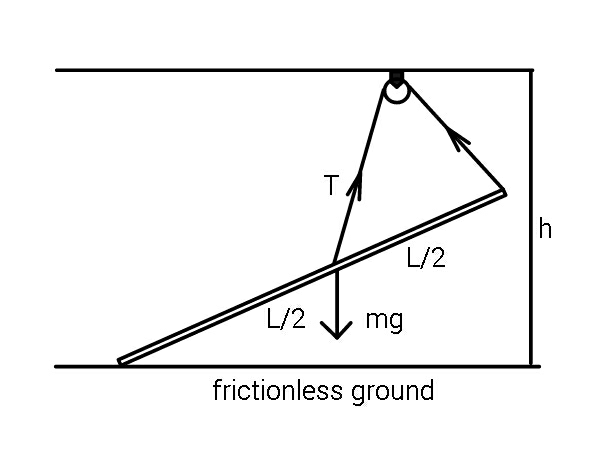
Answered by ajfour last updated on 15/Feb/20
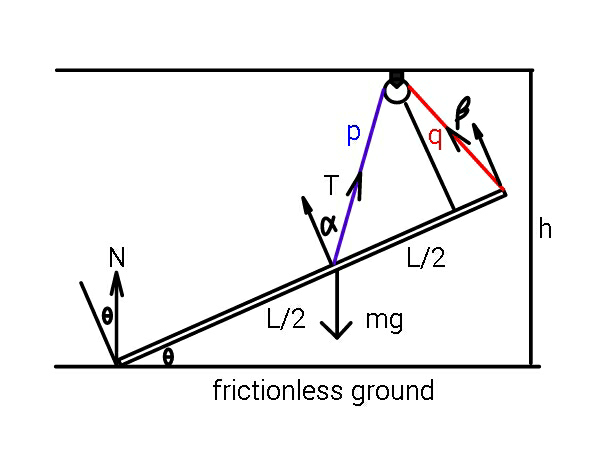
Commented by ajfour last updated on 15/Feb/20
$${I}\:{am}\:{enlisting}\:{just}\:{the}\:{eqs}. \\ $$$${that}\:{i}\:{have}: \\ $$$$\:\:\:\:{h}−\frac{{L}\:}{\mathrm{2}}\mathrm{sin}\:\theta={p}\mathrm{cos}\:\theta\:\:\:\:....\left({i}\right) \\ $$$$\:\:\:\:{h}−{L}\mathrm{sin}\:\theta={q}\mathrm{cos}\:\theta\:\:\:\:\:\:...\left({ii}\right) \\ $$$$\:\:\:\:{p}\mathrm{cos}\:\alpha={q}\mathrm{cos}\:\beta \\ $$$$\:\:\:\:{p}\mathrm{sin}\:\alpha+{q}\mathrm{sin}\:\beta=\frac{{L}}{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{cos}\:\alpha+\mathrm{2cos}\:\beta=\mathrm{5cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\alpha−\beta\:=\:\mathrm{2}\theta \\ $$$$\left({one}\:{of}\:{them}\:{is}\:{is}\:{dependent}\right) \\ $$$$\mathrm{cos}\:\alpha+\frac{\mathrm{2}{p}\mathrm{cos}\:\alpha}{{q}}=\mathrm{5cos}\:\theta \\ $$$$\Rightarrow\:\:\:\mathrm{cos}\:\alpha=\frac{\mathrm{5cos}\:\theta}{\left(\mathrm{1}+\mathrm{2}{p}/{q}\right)} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{cos}\:\beta=\frac{\mathrm{5}\left({p}/{q}\right)\mathrm{cos}\:\theta}{\left(\mathrm{1}+\mathrm{2}{p}/{q}\right)} \\ $$$$ \\ $$$$\:\:{p}\sqrt{\mathrm{1}−\left\{\frac{\mathrm{5cos}\:\theta}{\left(\mathrm{1}+\mathrm{2}{p}/{q}\right)}\right\}^{\mathrm{2}} }+ \\ $$$$\:\:\:\:{q}\sqrt{\mathrm{1}−\left\{\frac{\mathrm{5}\left({p}/{q}\right)\mathrm{cos}\:\theta}{\left(\mathrm{1}+\mathrm{2}{p}/{q}\right)}\right\}^{\mathrm{2}} }\:=\frac{{L}}{\mathrm{2}} \\ $$$${while}\:{we}\:{have}\:{p}\left(\theta\right)\:{and}\:{q}\left(\theta\right), \\ $$$${from}\:{first}\:{two}\:{eqs}. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$