
Question and Answers Forum
Question Number 81966 by naka3546 last updated on 17/Feb/20
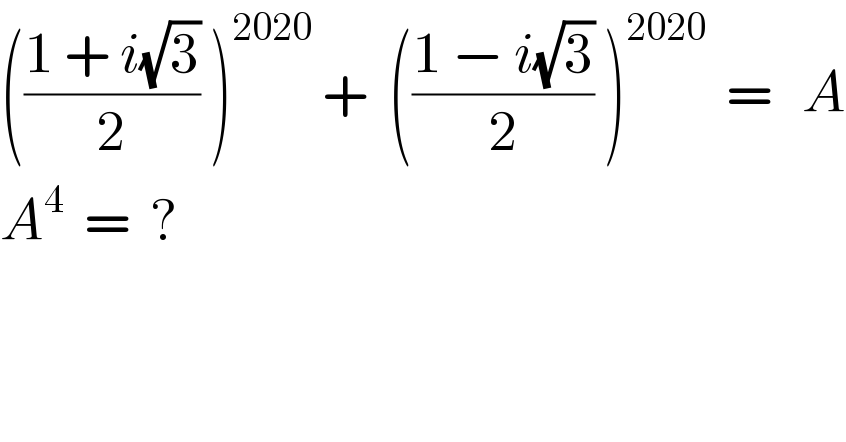
Answered by TANMAY PANACEA last updated on 17/Feb/20
![(1/2)=cos(π/3) ((√3)/2)=sin(π/3) (cos(π/3)+isin(π/3))^(2020) +(cos(π/3)−isin(π/3))^(2020) (e^(i×(π/3)) )^(2020) +(e^(−i×(π/3)) )^(2020) e^(iθ) +e^(−iθ) =2cosθ where[θ=((2020π)/3)] A=2cosθ A^4 =16(cosθ)^4 now cos(((2020π)/3)) cos(2020×60) =cos(121200) =cos(336×360+240) =−cos60 =((−1)/2) so required answer is16× (((−1)/2))^4 =1](Q81967.png)
Commented by naka3546 last updated on 17/Feb/20
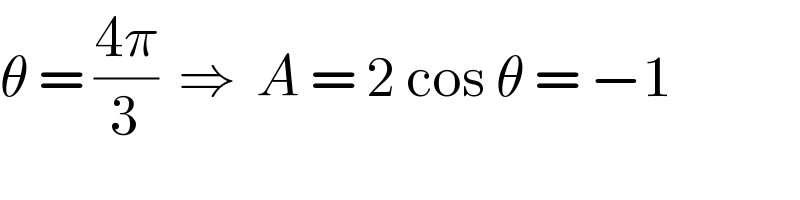
| ||
Question and Answers Forum | ||
Question Number 81966 by naka3546 last updated on 17/Feb/20 | ||
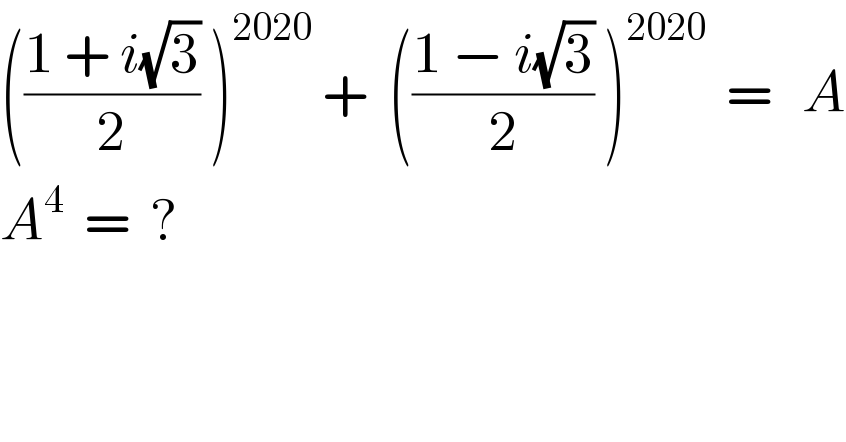 | ||
Answered by TANMAY PANACEA last updated on 17/Feb/20 | ||
![(1/2)=cos(π/3) ((√3)/2)=sin(π/3) (cos(π/3)+isin(π/3))^(2020) +(cos(π/3)−isin(π/3))^(2020) (e^(i×(π/3)) )^(2020) +(e^(−i×(π/3)) )^(2020) e^(iθ) +e^(−iθ) =2cosθ where[θ=((2020π)/3)] A=2cosθ A^4 =16(cosθ)^4 now cos(((2020π)/3)) cos(2020×60) =cos(121200) =cos(336×360+240) =−cos60 =((−1)/2) so required answer is16× (((−1)/2))^4 =1](Q81967.png) | ||
| ||
Commented by naka3546 last updated on 17/Feb/20 | ||
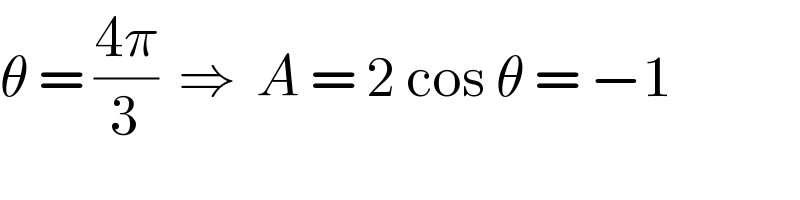 | ||