
Question and Answers Forum
Question Number 82160 by M±th+et£s last updated on 18/Feb/20
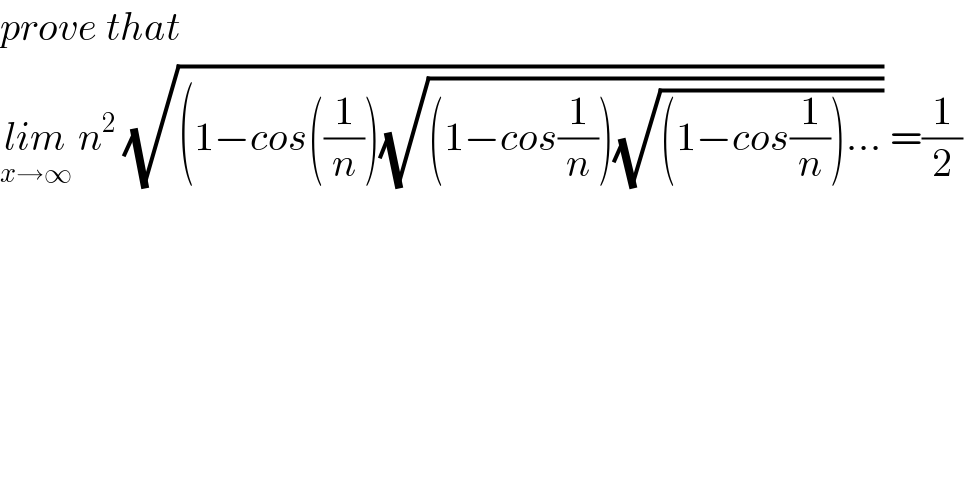
Answered by MJS last updated on 18/Feb/20
![w=(√((1−cos (1/n))(√((1−cos (1/n))(√(...)))))) w^2 =(1−cos (1/n))w ⇒ w=0∨w=1−cos (1/n) ...=lim_(n→∞) n^2 (1−cos (1/n)) let n=(1/k) lim_(k→0) ((1−cos k)/k^2 ) =lim_(k→0) (((d^2 /dk^2 )[1−cos k])/((d^2 /dk^2 )[k^2 ])) = =lim_(k→0) ((cos k)/2) =(1/2)](Q82166.png)
Answered by mr W last updated on 18/Feb/20
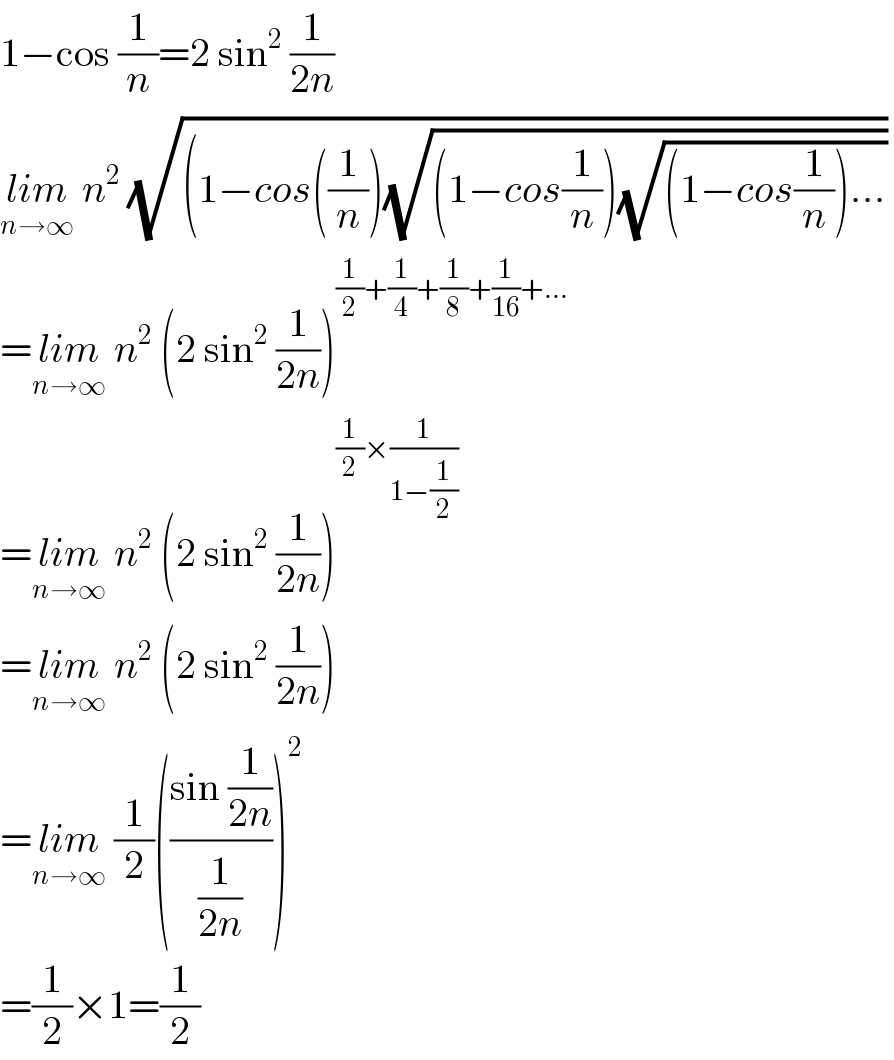
| ||
Question and Answers Forum | ||
Question Number 82160 by M±th+et£s last updated on 18/Feb/20 | ||
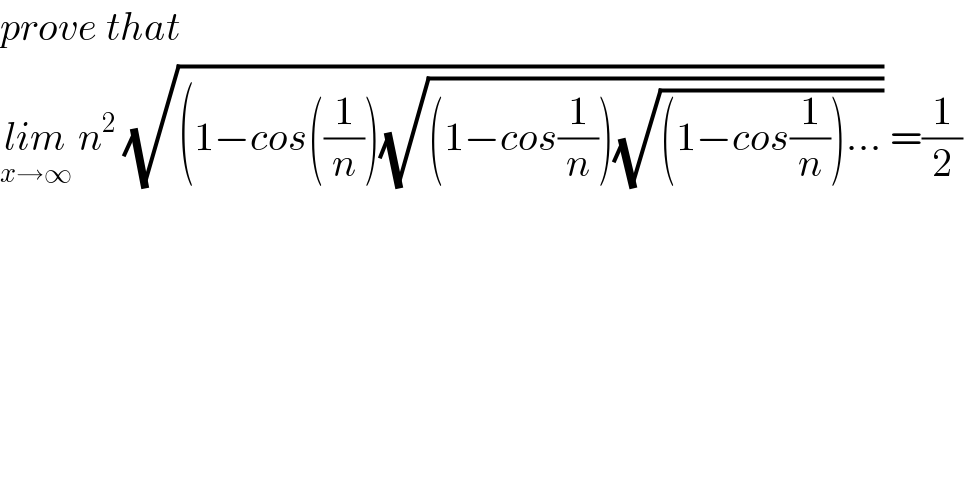 | ||
Answered by MJS last updated on 18/Feb/20 | ||
![w=(√((1−cos (1/n))(√((1−cos (1/n))(√(...)))))) w^2 =(1−cos (1/n))w ⇒ w=0∨w=1−cos (1/n) ...=lim_(n→∞) n^2 (1−cos (1/n)) let n=(1/k) lim_(k→0) ((1−cos k)/k^2 ) =lim_(k→0) (((d^2 /dk^2 )[1−cos k])/((d^2 /dk^2 )[k^2 ])) = =lim_(k→0) ((cos k)/2) =(1/2)](Q82166.png) | ||
| ||
Answered by mr W last updated on 18/Feb/20 | ||
 | ||
| ||